目录
- 栈的基本内容
- 顺序栈
- 定义
- 入栈操作
- 出栈
- 顺序栈的缺点
- 出栈顺序的计算方法
- 链栈
栈的基本内容
无论是我们接下来要讲的栈还是后面要讲到的队列,他们虽然在名字上不同于我们之前的顺序表或者单链表,但是它们本质也是线性表,只是在基本操作上没有表那么“自由”。比如:栈只能从栈顶进行插入和删除,而队列只能从对头进行删除,队尾进行插入。
举例:
叠放在一起的盘子,当想要加入新的盘子时,只能在底部或者尾部加入,删除同样也是。

空栈:
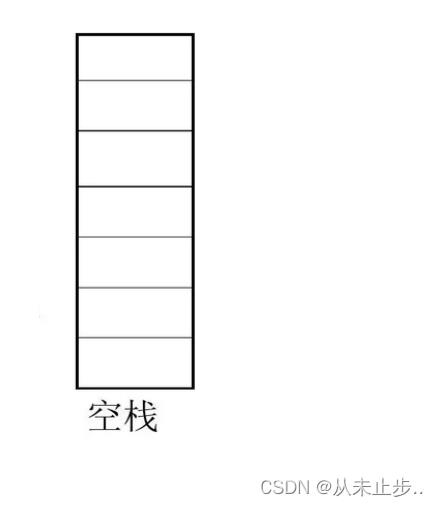
栈顶和栈底:
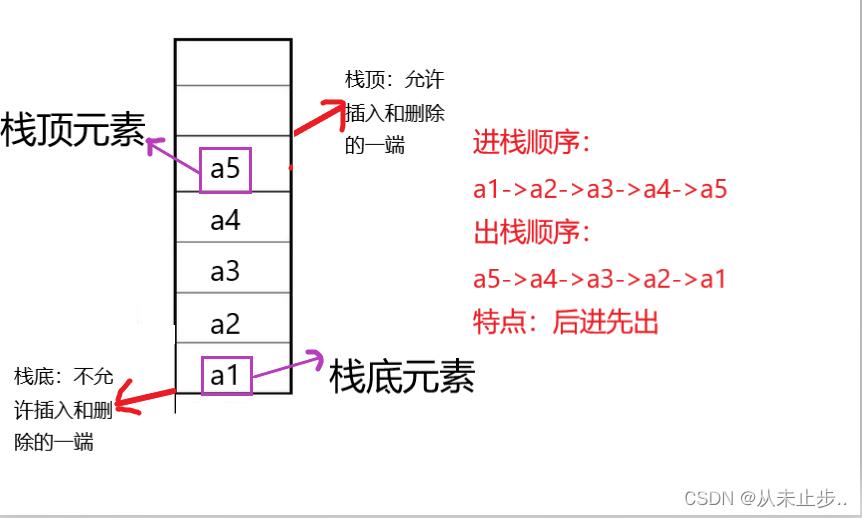
顺序栈
既然上文都说到“栈”和“队列”都是一种“特殊的”线性表”,那么顺序栈,顾名思义就是按照顺序存储的栈。
定义
既然是顺序存储的,那么我们依然可以和顺序表相类似,采用数组去存放!
typedef struct {
int data[size];
int top;//栈顶指针
}seqstack;//seqstack为结构体类型
入栈操作
对于顺序表的插入操作,我们在栈中叫做“入栈”,由于栈的特殊性,只能在栈顶进行操作。
需要提醒的是:一定是栈顶指针先进行移动,再将新插入的元素赋给栈顶空间。也就是说S.top = S.top + 1;S.data[S.top] = x;的顺序不能发生颠倒。
void Pushstack(seqstack& S)
{
if (S.top == size)
printf("栈满,拒绝元素继续入栈!");
else {
printf("请依次输入你要入栈的元素:\n");
int x,i;
for (i = 0; i < size; i++) {
scanf("%d", &x);
S.top = S.top + 1;
S.data[S.top] = x;
printf("入栈成功!\n");
}
}
}
举例:

出栈
虽然是“出栈”,但是如果后续没有入栈操作对出栈位置进行数据覆盖的话,其实出栈并不是真正意义上的“消失”,只是在逻辑上上被删除了,其实给出下标地址,依然可以找到该元素。**return S.data[S.top];**就是将该元素的值返回,以便下次能够快速找到。
int PopStack(seqstack& S) {
if (S.top == -1) {
printf("栈为空,没有元素输出!");
}
{
printf("当前栈顶元素为:");
return S.data[S.top];
S.top = S.top - 1;
}
}
关于顺序栈的其他操作都是比较简单的,这里就不一一进行讲解了,需要注意的事项我会在下面的完整代码中注释出来!
顺序栈的缺点
栈的大小不可发生变化。
出栈顺序的计算方法

如上图所示:
进栈顺序为a->b->c->d->e,则对应的出栈顺序为e->d->c->b->a
但有时候出栈和进栈是穿插进行的:
举例:

这种进栈出栈穿插的方式有很多种。
由此,我们可以得出一个结论:

链栈
既然上文都说到“栈”和“队列”都是一种“特殊的”线性表”,那么链栈,顾名思义就是按照链式存储的栈。
基本实现方法和单链表相同,这里就不一一进行讲解了,需要注意的事项我会在下面的完整代码中注释出来!
链栈完整代码如下:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#define size 5
typedef struct LinkNode {
int data;
struct LinkNode* next;
}Linkstack;
//初始化
void Iniststack(Linkstack *L) {
L= (LinkNode*)malloc(sizeof(LinkNode));
if (!L->data) {
printf("申请失败");
}
else
{
L->data = 0;
L->next = NULL;
}
}
//入栈
void Pushstack(Linkstack *L) {
int e,x;
printf("请输入你要创建的链栈长度:");
scanf("%d", &x);
printf("请输入你要入栈的元素:\n");
for (int i = 0; i < x; i++) {
LinkNode* s = (LinkNode*)malloc(sizeof(LinkNode));
scanf("%d", &e);
s->data = e;
s->next = L->next;
L->next = s;
}
}
//出栈
int Popstack(Linkstack* L)
{
LinkNode* s= L->next;
s->data = L->data;
L->next = s->next;
return s->data;
}
//读取栈顶元素
int Getstack(Linkstack* L) {
if (!L->data)
{
printf("栈为空!");
}
else {
int e = L->next->data;
return e;
}
}
//输出栈中元素
void Printsatck(Linkstack* L) {
if (!L->data)
{
printf("栈为空!");
}
else {
LinkNode* p;
p = L;
printf("栈中元素如下:");
while (p)
{
p = p->next;
printf("%d", p->data);
}
}
}
int main() {
Linkstack L;
Iniststack(&L);
Pushstack(&L);
Popstack(&L);
Getstack(&L);
Printsatck(&L);
}
输出:
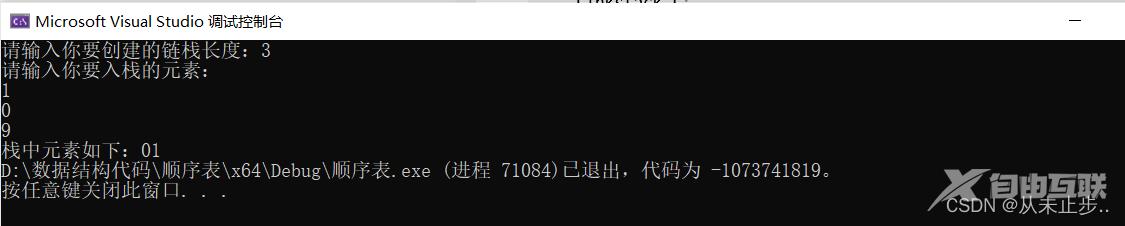
顺序栈完整代码如下:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#define size 5
typedef struct {
int data[size];
int top;
}seqstack;
//初始化操作
void InistStack(seqstack &S) {
S.top = -1;
}
//判空操作
void IsEmpty(seqstack& S)
{
if (S.top == -1)
printf("目前栈为空!\n");
}
//入栈操作
void Pushstack(seqstack& S)
{
if (S.top == size)
printf("栈满,拒绝元素继续入栈!");
else {
printf("请依次输入你要入栈的元素:\n");
int x,i;
for (i = 0; i < size; i++) {
scanf("%d", &x);
S.top = S.top + 1;
S.data[S.top] = x;
printf("入栈成功!\n");
}
}
}
//读取栈顶元素
void Getstack(seqstack& S) {
if (S.top == -1) {
printf("栈为空,没有元素输出!");
}
{
printf("当前栈顶元素为:");
printf("%d\n", S.data[S.top]);
}
}
//输出栈中元素
void Printstack(seqstack& S) {
if (S.top == -1) {
printf("栈为空,没有元素输出!");
}
else {
printf("栈中元素如下:");
for (int i = 0; i < size; i++) {
printf("%d", S.data[i]);
}
printf("\n");
}
}
//出栈
int PopStack(seqstack& S) {
if (S.top == -1) {
printf("栈为空,没有元素输出!");
}
{
printf("当前栈顶元素为:");
return S.data[S.top];
S.top = S.top - 1;
}
}
//删除栈顶元素
int Deletestack(seqstack& S) {
if (S.top == -1) {
printf("栈为空!\n");
}
else
{
int e;
for (int i = 0; i < size; i++) {
e = S.data[S.top];
S.top = S.top - 1;
return e;
}
printf("所有元素已被删除!\n");
}
}
//清栈
void Clearstack(seqstack& S) {
S.top = -1;
printf("栈已经被清空!\n");
}
int main() {
seqstack S;
int x;
InistStack(S);
IsEmpty(S);
Pushstack(S);
Getstack(S);
Printstack(S);
/*x=PopStack(S);*/
Deletestack(S);
Clearstack(S);
Printstack(S);
}
输出:
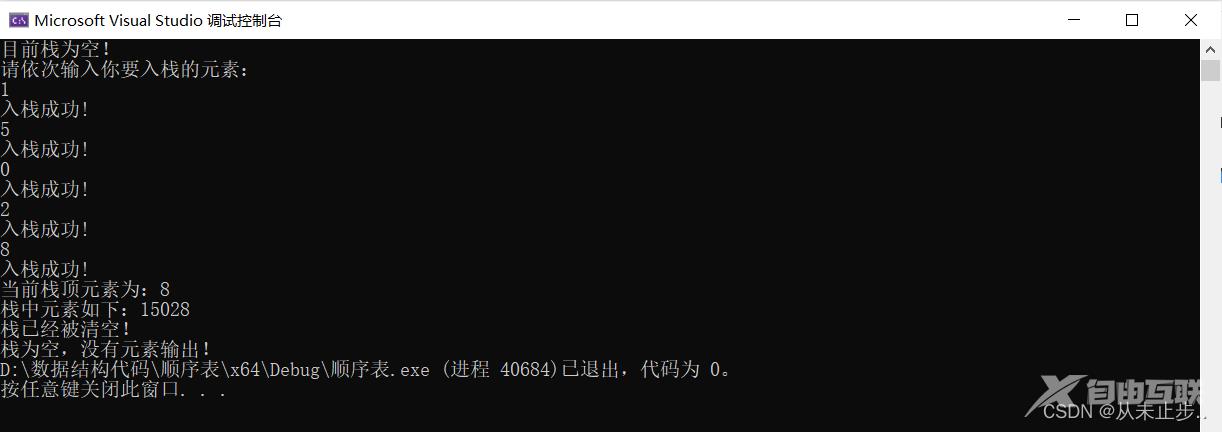
以上就是C语言中顺序栈和链栈的定义和使用详解的详细内容,更多关于C语言顺序栈 链栈的资料请关注自由互联其它相关文章!
