C语言折半查找法介绍及使用示例

目录

• 1. 折半查找介绍
• 1.1 定义
• 1.2 基本原理
• 1.3 时间复杂度与空间复杂度
• 1.4 优缺点
• 2. 代码实现
• 2.1 代码设计
• 2.2 代码实现

1. 折半查找介绍

1.1 定义

折半查找也称二分查找，是一种在有序数组中查找某一特定元素的搜索算法，每一次查找，搜索范围均缩小一半，效率较高。如果数组是乱序状态，则应排序，再进行查找。

1.2 基本原理

搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半 。

1.3 时间复杂度与空间复杂度

总共有n个元素，每次查找的区间大小就是n，n/2，n/4，…，n/ 2 k 2^k 2k，一直到1，其中k就是循环的次数。

由于n/ 2 k 2 ^ k 2k取整后>=1，即令n/ 2 k 2^k 2k=1，可得k=log2n,（是以2为底，n的对数），所以时间复杂度可以表示O()=O(logn)。

二分查找只需要额外存储三个变量：最大值 ，最小值 和 中点，空间复杂度为常数 O(1)。

1.4 优缺点

优点：比较次数少，查找速度快，平均性能好。

缺点：要求待查表为有序表，且插入删除困难。

2. 代码实现

2.1 代码设计

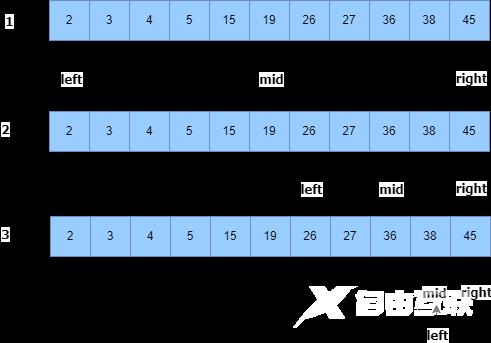
1. 输入需要查找的元素，我们输入的是38；left是有序数组最左端0，是最小值，right是有序数组最右端10，是最大值，mid为数组1/2位置，即array[5]；
2. 38比array[5] = 19大，因此left等于原mid+1，即array[6] = 26，right不变；新mid为(left+right)/2 = （6+10）/2 = 8；
3. 38比array[8] = 36大，因此left等于上一次mid+1，即array[9] = 38，right不变；新mid为(left+right)/2 = （9+10）/2 = 9；
4. 38等于array[9]，mid与left重合， 查找成功，返回数组下标9.

2.2 代码实现

#include <stdio.h>
#include <string.h>
int binarySearch(int array[],int len,int target){
    int left = 0;
    int right = len - 1;
    while(left <= right){
        int mid = (right + left) / 2;
        if(array[mid] == target){
            return mid;
        } else if(array[mid] < target){
            left = mid + 1;
        } else if(array[mid] > target){
            right = mid - 1;
        }
    }
    return -1;
}
int main(void)
{
    int array[]={2,3,4,5,15,19,26,27,36,38,45};
    int key = 0,ret;
    printf("请输入需要查找的数字:");
    scanf("%d",&key);
    ret = binarySearch(array,sizeof(array)/sizeof(int),key);
    if(ret < 0)
        printf("查找失败\n");
    else
        printf("该数字为数组第%d个元素\n",ret+1);
    return 0;
}

运行结果：

请输入需要查找的数字:38

该数字为数组第10个元素

到此这篇关于C语言折半查找法介绍及使用示例的文章就介绍到这了,更多相关C语言折半查找内容请搜索自由互联以前的文章或继续浏览下面的相关文章希望大家以后多多支持自由互联！