数据结构——线段树

一、概述

线段树是一种二叉搜索树，其存储的是一个区间的信息，每个结点以结构体的形式去存储，每个结构体包含三个元素：区间左端点、区间右端点、该区间要维护的信息（视实际情况而定），其基本思想是分治的思想。

 

其特点是：

• 每个节点的左孩子区间范围为 [l，mid]，右孩子为 [mid+1,r]
• 对于结点 k，左孩子结点为 2 * index + 1，右孩子为 2 * index + 2，符合完全二叉树的性质。
• 线段树不是完全二叉树。
• 线段树是平衡二叉树。

二、线段树

2.1 使用数组构建线段树

如下图所示数组A，以求和为例：根节点A[0-7]存放的就是A[0-3]节点和A[4-7]节点之和，下面的每个节点存放的值都是该节点对应左右孩子节点的和，这样就用数组构建出了一个线段树。

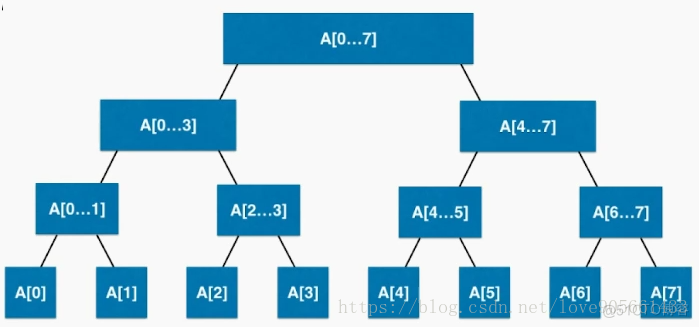
• 可以把线段树当成满二叉树进行处理。
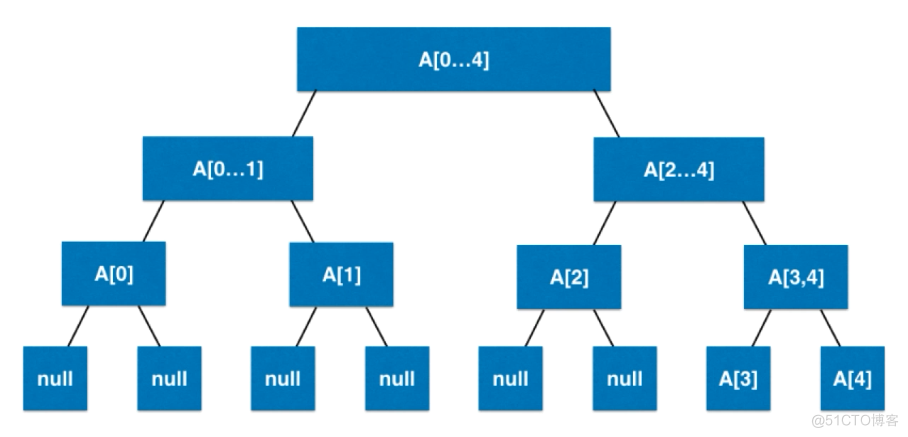
• 对于有n个元素的区间，数组只需要4n的空间就可以完全存储整颗线段树，4n的空间会有部分浪费，最坏的情况可能会有接近2n的空间被浪费。
• 不考虑添加元素。

2.2 线段树区间查找

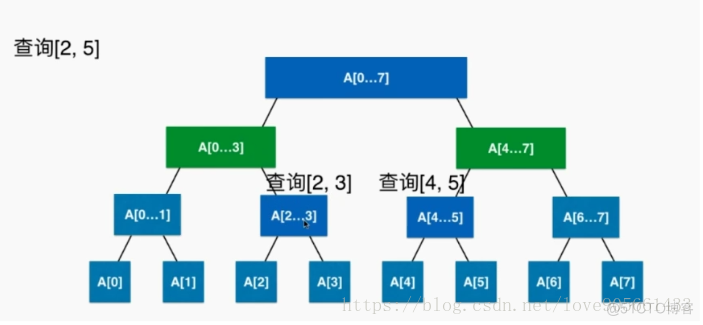
如下图所示, 线段树查找步骤如下:

• 1、在0-7的区间内查找2-5，左右子树都包含部分，所以在左侧查询2-3，右侧查询4-5。
• 2、继续在0-3的区间查找2-3，在4-7的区间查找4-5。
• 3、将查找到的2-3区间和4-5区间进行一次merge操作，得到的就是2-5的区间。

2.3 线段树更新

线段树更新的方法也很简单，更新对应位置的值之后，包含该位置的区间的值也都要进行更新。

三、线段树代码实现

3.1 线段树完整代码实现如下

/** * @Author: huangyibo * @Date: 2022/2/24 21:33 * @Description: 线段树 */ public class SegmentTree<E> { //线段树，底层数组实现 private E[] tree; //原数组副本 private E[] data; private Merger<E> merger; public SegmentTree(E[] arr, Merger<E> merger){ this.merger = merger; this.data = (E[])new Object[arr.length]; for (int i = 0; i < arr.length; i++) { data[i] = arr[i]; } // 对于有n个元素的区间, 使用数组实现线段树的话, 需要4n的空间来存储 this.tree = (E[])new Object[arr.length * 4]; //构建线段树 buildSegmentTree(0, 0, data.length - 1); } /** * 在treeIndex的位置创建表示区间[left, right]的线段树 * @param treeIndex 根节点所在的索引 * @param left treeIndex对应的左端点 * @param right treeIndex对应的右端点 */ private void buildSegmentTree(int treeIndex, int left, int right){ // 递归到底的情况 if (left == right){ //区间长度为1, 只有一个元素的时候 //此时节点存储的信息就是该节点本身 tree[treeIndex] = data[left]; return; } //treeIndex为根节点的左孩子节点索引 int leftTreeIndex = leftChild(treeIndex); //treeIndex为根节点的右孩子点索引 int rightTreeIndex = rightChild(treeIndex); int mid = (left + right) >>> 1; //以leftTreeIndex为根节点，创建表示区间[left, mid]的线段树 buildSegmentTree(leftTreeIndex, left, mid); //以rightTreeIndex为根节点，创建表示区间[mid + 1, right]的线段树 buildSegmentTree(rightTreeIndex, mid + 1, right); //具体的业务相关数据，综合左、右两个线段数据，得到其根节点的信息 //可以是、最大值、最小值、和、乘积等等 tree[treeIndex] = merger.merger(tree[leftTreeIndex], tree[rightTreeIndex]); } public int getSize(){ return data.length; } public E get(int index){ if(index < 0 || index >= data.length){ throw new IllegalArgumentException("index is illegal."); } return data[index]; } /** * 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引 * @param index * @return */ private int leftChild(int index){ return 2 * index + 1; } /** * 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引 * @param index * @return */ private int rightChild(int index){ return 2 * index + 2; } /** * 返回区间[queryL, queryR]的值 * @param queryL * @param queryR * @return */ public E query(int queryL, int queryR){ if(queryL < 0 || queryL >= data.length || queryR < 0 || queryR >= data.length || queryL > queryR){ throw new IllegalArgumentException("index is illegal."); } return query(0, 0, data.length - 1, queryL, queryR); } /** * 在以treeIndex为根的线段树中[left, right]的范围里，搜索区间[queryL, queryR]的值 * @param treeIndex * @param left * @param right * @param queryL * @param queryR * @return */ private E query(int treeIndex, int left, int right, int queryL, int queryR){ //如果查询区间值和treeIndex的左右区间值重合，直接返回 if(left == queryL && right == queryR){ return tree[treeIndex]; } int mid = (left + right) >>> 1; //treeIndex为根节点的左孩子节点索引 int leftTreeIndex = leftChild(treeIndex); //treeIndex为根节点的右孩子点索引 int rightTreeIndex = rightChild(treeIndex); // 要查找的区间左边界大于mid时, 说明只需要到右子树进行查找即可 if(queryL >= mid + 1){ return query(rightTreeIndex, mid + 1, right, queryL, queryR); }else if(queryR <= mid){ // 要查找的区间右边界小于等于mid时, 说明只需要到左子树进行查找即可 return query(leftTreeIndex, left, mid, queryL, queryR); } //queryL < mid < queryR 的情况, 需要对左右子树分别进行查找 E leftResult = query(leftTreeIndex, left, mid, queryL, mid); E rightResult = query(rightTreeIndex, mid + 1, right, mid + 1, queryR); //进行融合操作 return merger.merger(leftResult, rightResult); } /** * 将index索引的值, 更新为e * @param index * @param e */ public void set(int index, E e){ if(index < 0 || index >= data.length){ throw new IllegalArgumentException("index is illegal."); } data[index] = e; //在以treeIndex为根的线段树中[left, right]的范围里，更新index的值 set(0, 0, data.length - 1, index, e); } /** * 在以treeIndex为根的线段树中[left, right]的范围里，更新index的值 * @param treeIndex * @param left * @param right * @param index * @param e */ private void set(int treeIndex, int left, int right, int index, E e){ // 递归终止条件 //如果查询区间值和treeIndex的左右区间值重合，直接更新元素e if (left == right) { tree[treeIndex] = e; return; } int mid = (left + right) >>> 1; //treeIndex为根节点的左孩子节点索引 int leftTreeIndex = leftChild(treeIndex); //treeIndex为根节点的右孩子点索引 int rightTreeIndex = rightChild(treeIndex); // 要查找的index大于mid时, 说明只需要到右子树进行查找即可 if(index >= mid + 1){ set(rightTreeIndex, mid + 1, right, index, e); }else { //index <= mid // 要查找的index小于等于mid时, 说明只需要到左子树进行查找即可 set(leftTreeIndex, left, mid, index, e); } //更新完值之后，对更新相关的每一层的根节点重新进行融合操作 tree[treeIndex] = merger.merger(tree[leftTreeIndex], tree[rightTreeIndex]); } @Override public String toString() { StringBuilder res = new StringBuilder(); res.append("["); for (int i = 0; i < tree.length; i++) { if(tree[i] != null){ res.append(tree[i]); }else { res.append("null"); } if(i != tree.length - 1){ res.append(", "); } } res.append("]"); return res.toString(); } }

3.2 使用的merger融合器代码如下 :

/** * @Author: huangyibo * @Date: 2022/2/24 22:08 * @Description: 对元素的融合操作 * 用于将两个元素融合成一个元素, 配合线段树的合并操作使用 * @FunctionalInterface这个注解是jdk8中函数式接口声明, 加不加不影响 */ @FunctionalInterface public interface Merger<E> { E merger(E a, E b); }

3.3 简单测试的代码如下

public class Test { public static void main(String[] args) { Integer[] nums = {-2, 0, 3, -5, 2, -1}; SegmentTree<Integer> segmentTree = new SegmentTree<>(nums, (a, b) -> a + b); System.out.println(segmentTree); System.out.println(segmentTree.query(0,2)); System.out.println(segmentTree.query(2,5)); System.out.println(segmentTree.query(1,4)); System.out.println(segmentTree.query(0,5)); } }

参考： https://blog.csdn.net/love905661433/article/details/83006902