符号约定
贝叶斯分类器
基于最小错误率的决策
符号约定:
- 样本 \(\boldsymbol{x}\in R^d\)
- 状态(类) \(w = {w_1,w_2,\dots}\)
- 先验概率 \(P(w_1),P(w_2)\)
- 样本分布密度 \(p(x)\)
- 类条件概率密度 \(p(\boldsymbol{x}|w_1),p(\boldsymbol{x}|w_2)\)
- 后验概率 \(P(w_1|\boldsymbol{x}),P(w_2|\boldsymbol{x})\)
- 错误概率\[P(e|\boldsymbol{x})\lbrace_{P(W_1|\boldsymbol{X}) \ if\ \boldsymbol{x}\ is\ assigned\ to\ w_2}^{P(W_2|\boldsymbol{X})\ if\ \boldsymbol{x}\ is\ assigned\ to\ w_1}\]
- 平均错误率 \(P(e) = \int P(e|\boldsymbol{x})p(\boldsymbol{x})d\boldsymbol{x}\)
- 正确率 \(P(c)\)
策略:错误概率最小嘛,很简单易懂
\[P(e|\boldsymbol{x})\lbrace_{P(W_1|\boldsymbol{X}), \ if\ P(w_1|\boldsymbol{x})>P(w_2|\boldsymbol{x})}^{P(W_2|\boldsymbol{X}), \ if\ P(w_1|\boldsymbol{x})所以:\(x\) 属于那种状态时的错误概率小,就认为 \(x\) 是那种状态
基于最小风险的决策
- 符号约定:
- 样本 \(\boldsymbol{x}\in R^d\)
- 状态(类) \(w = {w_1,w_2,\dots}\)
- 决策, \(\alpha_i\) 表示将样本分类为 \(w_j,j\in1,\dots,n\)
- 将真实标记为 \(w_j\) 的样本误分类为 \(w_i\) 所产生的损失 \(\lambda_{i,j}\)
- 对于特定 \(x\) 采取决策 \(\alpha_i\) 的期望损失(基于后验概率 \(P(w_i|\boldsymbol{x})\) )\[R(\alpha_i|\boldsymbol{x}) = \sum_{j=1}^{N}\lambda_{ij}P(w_j|\boldsymbol{x})\]
- 期望风险,即对 \(x\) 所有可能的决策 \(\alpha(x)\) 所造成的期望损失之和,也称为平均风险\[R(\alpha) = \int R(\alpha(x)|x)p(x)dx\]
- 策略:使 \(R(\alpha(x)|x)\) 最小
线性判别函数
思路:直接利用样本集设计分类器。
\[g(x) = w^Tx+w_0\]\[w^Tx+w_0 \geq 0 \Rightarrow x \in C_1\]\[w^Tx+w_0 <0\Rightarrow x \in C_2 \]- 对于 c 类分类问题:
- 设 \(g_i(\boldsymbol{x}),i = 1,2,\cdots,c\) 表示每个类别对应的判别函数
- 决策规则:
- 如果 \(g_i(\boldsymbol{x})>g_j(\boldsymbol{x}),\forall j \ne i\),则 \(\boldsymbol{x}\) 被分到第 \(i\) 类
- 对于两类分类问题:
- 可以只用一个判别函数:\(g(\boldsymbol{x})=g_1(\boldsymbol{x})-g_2(\boldsymbol{x})\)
- 判别准则:\(g(\boldsymbol{x})>0\),分为第一类;否则分为第二类
- 此时,\(g(\boldsymbol{x})=0\) 定义了一个决策面,它是类 \(C_1\) 与 \(C_2\) 的分界面
如果 \(\boldsymbol{x_1}\) 和 \(\boldsymbol{x_2}\) 都在决策面上,则有 \(w^Tx_1+w_0 = w^Tx_2+w_0\),即 \(w^T(x_1-x_2)=0\),说明 \(w\) 为该决策面的法向量
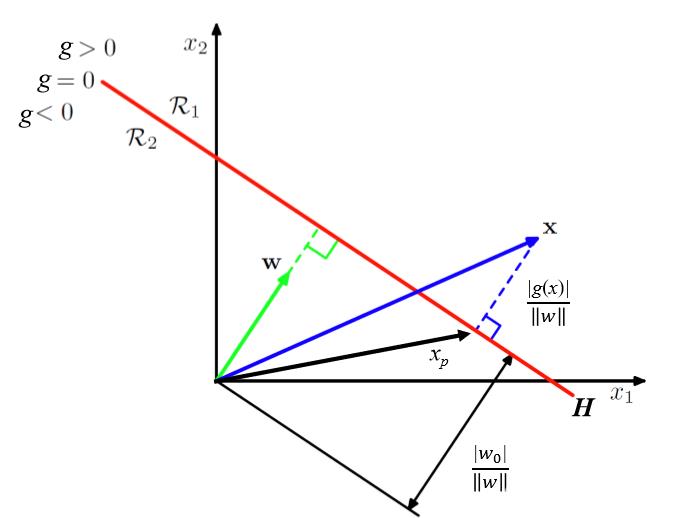
判别函数 \(g(\boldsymbol{x})\) 可以看成是特征空间中某点 \(x\) 到超平面距离的一种代数度量:
\[x = x_p + r \frac{w}{||w||}\]\[g(x) = w^T(x_p + r \frac{w}{||w||})+w_0 = r||w||\]- \(x_p\):\(x\)在决策面上的投影向量
- \(r\):\(x\)到决策面的垂直距离
- \(\frac{w}{||w||}\):\(w\)方向上的单位向量
广义线性判别函数(就举个例子)
对于二分类问题,\(\boldsymbol{X}是一维样本空间\)
若 \(x 或 \(x > b\) 时,\(x \in w_1\);\(a 可使 \(g(x) = (x-a)(x-b)\) 可写为 \(g(x) = c_0+c_+c_2x^2\) 可转化为 \(g(x) = \boldsymbol{c}^Ty = \sum_{i = 1}^{3}c_iy_i\) 其中 \(y_1 = 1,y_2 = x,y_3 = x^2\)
线性分类器设计
Fisher 准则
考虑把d维空间的样本投影到一条直线上形成一维空间。在一般情况下总可以找到某个方向,使样本在这个方向的直线上的投影分开得最好。(即寻找最好投影方向的问题)
以二分类为例,\(d\) 维样本 \(x_1,x_2\cdots,x_n\),其中 \(N_1\) 个属于 \(w_1\) 类,记为子集 \(X_1\),\(N_2\) 个属于 \(w_2\) 类,记为子集 \(X_2\)
定义样本在d维特征空间的描述量
求出各类样本的均值向量 \(m_i = \frac{1}{N_i}\sum_{x\in X_i}x,i = 1,2\)
求出样本类内离散度矩阵 \(S_i\) 和总类内离散度矩阵 \(S_w\)
\[S_i =\sum_{x\in X_i}(x-m_i)(x-m_i)^T,i = 1,2\]\(S_w = S_1 + S_2\) 或 \(S_w = P(w_1)S_1 + P(w_2)S_2\)
求出样本类间离散度矩阵 \(S_b\)
\(S_b = (m_1-m_2)(m_1-m_2)^T\) 或 \(S_b = P(w_1)P(w_2)(m_1-m_2)(m_1-m_2)^T\)
在一维Y空间内
- 求出各类样本均值 \(\tilde{m_i} = \frac{1}{N_i}\sum_{y\in\eta_i}y,i = 1,2\)
- 求出样本类内离散度 \(\tilde{S^2_i}\) 和总类内离散度 \(\tilde{S_w}\)\[\tilde{S^2_i} = \sum_{y\in\eta_i}(y-\tilde{m_i})^2,i = 1,2\]\[\tilde{S_w} = \tilde{S^2_1} + \tilde{S^2_2}\]
使用这些量,我们可以给出Fisher准则的函数形式:
- 投影后在一维Y空间中各类样本尽可能分开,即两类均值之差越大越好
- 各类样本内部尽量幂级,即类内离散度越小越好
即求使得:
\[J_F(w) = \frac{(\tilde{m_1}-\tilde{m_2})^2}{\tilde{S^2_1}+\tilde{S^2_2}} = \frac{w^TS_bw}{w^TS_ww}\]取得最大值的 \(w\) ,解得 \(w^* = S^{-1}_w(m_1-m_2)\)
感知机准则
一组容量为\(N\)的样本集\(y_1,y_2,\cdots y_N\),其中\(y_n\) 为 \(d\) 维增广样本向量,分别来自 \(w_1\) 类和 \(w_2\) 类。如果存在权向量 \(a\),使得对于任何\(y\in w_1\),都有 \(a^Ty > 0\),而对于任何 \(y \in w_2\) 有 \(a^Ty <0\), 则称这组样本为线性可分的,反之亦然成立。
首先进行样本规范化:
\[y^{'}_n = \lbrace^{y_i>0,y_i \in w_1}_{-y_j<0,y_j \in w_2} \]使得:
\[a^Ty^{'}_n>0\]求 \(a\):
构造准则函数 \(J_P(a) = \sum_{y \in \eta^k}(-a^Ty)\),其中 \(\eta^k\) 是被权向量 \(a\) 错分的样本集合,即当错分时,有 \(a^Ty^{'}_n<0\) ,易得,当且仅当 \(\eta^k\) 为空时,求得 \(a\)。
使用梯度下降法求解
\[\triangledown J_P(a) = \frac{\partial J_P(a)}{\partial a} = \sum_{y \in \eta^k}(-y)\]根据博客:https://blog.csdn.net/edison_03/article/details/72835485
我们都知道这种对所有错分样本放到一起进行修正的做法是不妥当的,更妥当的办法是对每一个错分样本都单独修正
因此,\(a(t+1) = a(t) + \rho_k y_i\),直到所有样本都被正确分类时终止迭代
最小二乘准则跟线性回归差不多,不写了
