二叉树的概念及结构
概念
一颗二叉树是结点的有限集合,该集合或者为空,或者由一个根节点加上两棵别称为左子树和右子树的二叉树的组成。

从上图可以看出:
1.二叉树不存在度大于2的结点;
2.二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
注意:对于任意的二叉树都是由以下几种情况复合而成的
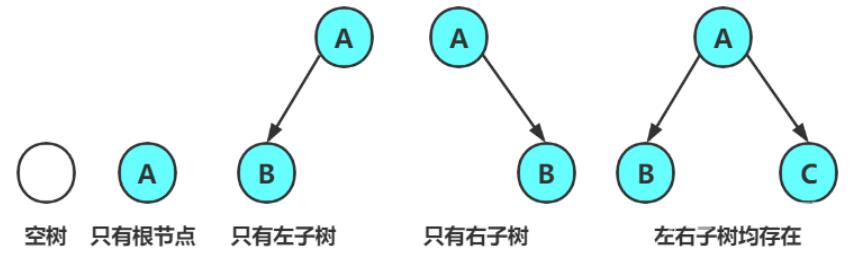
特殊的二叉树
满二叉树
满二叉树:一个二叉树,如果每一层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^k^-1,则它就是满二叉树。
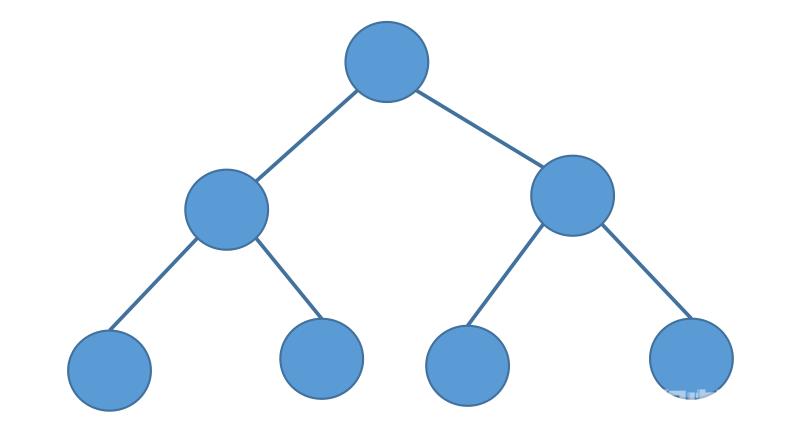
满二叉树中如果第k层满了,则第k层的结点个数是2^k-1^;如果满二叉树的深度为h,则满二叉树一共有2^h^-1个结点。
扩展:满二叉树第一层有一个结点即2^0^,第二层有2个结点2^1^,第三层有4个节点2^2^……所以第k层节点个数为2^k-1^。
当我们知道满二叉树的深度为h时,可以根据k层的结点个数通过错位相减推导出该满二叉树的结点个数。
结点个数为每层结点个数相加之和,从第一层开始:T(n) = 2^0^ + 2^1^ + 2^2^ + …… + 2^h-1^;乘以2:2T(n) = 2^1^ + 2^2^ + 2^3^ …… + 2^h^,相减之后可以求出该满二叉树一共有2^h^-1个结点。
完全二叉树
**完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 **
注意:满二叉树是一种特殊的完全二叉树。
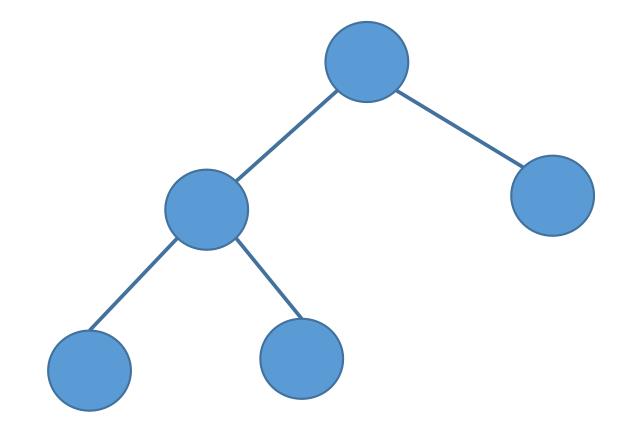
完全二叉树前N-1层都是满的,最后一层可以不满,但是必须从左到右是连续的。
假设完全二叉树的高度是h,则该完全二叉树最多情况下(即该完全二叉树是满二叉树)有2^h^-1个结点,最少情况下(即该完全二叉树第h层只有一个节点)有2^h-1^个结点。
扩展:推导最少情况下(即该完全二叉树第h层只有一个节点)有2^h-1^个结点
满二叉树时第h层有2^h-1^个结点,当该完全二叉树第h层只有一个节点时,完全二叉树节点个数最少,拿满二叉树的节点个数减去满二叉树最后一层的节点个数再加上1得到的就是完全二叉树节点最少的情况,即(2^h^-1) - (2^h-1)^ + 1 = 2^h-1^。
