递归的定义
递归:函数自己调用自己 大事化小
函数递归是有成本的
递归常见例题
1.接收一个整型值(无符号),按照顺序打印它的每一位
void print(unsigned int num)
{
if (num > 9)
{
print(num / 10);
}
printf("%d", num % 10);
}
int main()
{
unsigned int num = 0;
scanf("%u", &num);
print(num);
return 0;
}
//每一次递归都在逐步加深层次
//递归有一种循环的感觉
//不用递归的话这个题需要创建数组才能实现正序打印每一位
/* while (num)
{
printf("%d \n", num % 10);// 倒序 可以用数组先存起来在按顺序输出
num = num / 10;
}*/2.编写函数不允许创建临时变量,求字符串的长度
# include <stdio.h>
# include <string.h>
/*int my_strlen(char* str)
{
int count = 0;//创建了临时变量
while (*str != '\0')
{
count++;
str++;
}
return count;
}*/
int my_strlen(char* str)
{
if (*str != '\0')
{
return 1 + my_strlen(str+1);//err:str++ 先使用str 再自增 起不到作用 没法往里递归
}
return 0;
}
//大化小:字符串 大 -------> 最小:'\0' (只有一个\0) return 0;
//小:若干个字符+'\0' 至少有1个字符 return 1+my_strlen(str+1) 具体多少交给递归最简单有一个
int main()
{
char ch[] = "abcdef";
//方法1 库函数
//int len = strlen(ch);
//方法2 自定义函数 方法3 递归实现
int len = my_strlen(ch);
printf("%d", len);
return 0;
}
3.n!
#include <stdio.h>
int fact(int n)
{
if (n > 1)
{
return n * fact(n - 1);
}
else
{
return 1;
}
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = fact(n);
printf("%d", ret);
return 0;
}
//(由公式写出递归) 4.求第n个fib 1 1 2 3 5 8 13 21 34 55
#include <stdio.h>
int fib(int n)
{
if (n > 2)
return fib(n - 1) + fib(n - 2);
else
return 1;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("%d", ret);
}
//测试时:发现输入50 输出要花很长时间 原因是存在大量的重复计算 造成递归的层次太深 效率低下
//方法二:迭代
#include <stdio.h>
int fib(int n)
{
int a = 1;
int b = 1;//前两位
int c = 1;//输入n=1/2时返回1
while (n >= 3)
{
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("%d", ret);
return 0;
}
5 字符串逆序
//字符串逆序
#include <stdio.h>
#include <string.h>
int main()
{
char arr[] = { "abcdefg" };
int left = 0;
int right = strlen(arr) - 1;
while (left < right)
{
char tmp = arr[left];
arr[left] = arr[right];
arr[right] = tmp;
left++;
right--;
}
printf("%s", arr);
return 0;
}
//方法二:函数实现(迭代)
#include <stdio.h>
#include <string.h>
void reverse(char arr[])
{
int left = 0;
int right = strlen(arr) - 1;
while (left < right)
{
char tmp = arr[left];
arr[left] = arr[right];
arr[right] = tmp;
left++;
right--;
}
}
int main()
{
char arr[] = "abcdef";
reverse(arr);
printf("%s\n", arr);
return 0;
}
//方法三 递归实现1
#include <stdio.h>
#include <string.h>
void reverse(char* str)
{//逆序abcdef->交换af 逆序bcde -> 交换af,be 逆序cd
int len = strlen(str);
char tmp = *str;
*str = *(str + len - 1);
*(str + len - 1) = '\0';
if (strlen(str + 1) >= 2) //中间剩一个字符就不用逆序了
reverse(str + 1); //要加限制条件否则会死递归
*(str + len - 1) = tmp;
}
int main()
{
char arr[] = "abcdef";
reverse(arr);
printf("%s\n", arr);
return 0;
}
//方法三 递归实现2
#include <stdio.h>
void reverse(char arr[], int left, int right)
{//逆序abcdef->交换af 逆序bcde -> 交换af,be 逆序cd
if (left < right)
{
char tmp = arr[left];
arr[left] = arr[right];
arr[right] = tmp;
reverse(arr, left + 1, right - 1);
}
}
int my_strlen(char* str)
{
int count = 0;
while (*str != '\0')
{
count++;
str++;
}
return count;
}
int main()
{
char arr[] = "abcdef";
int left = 0;
int right = my_strlen(arr) - 1;
reverse(arr, left, right);
printf("%s\n", arr);
return 0;
}6 递归实现N的K次方
//递归实现N的K次方
#include <stdio.h>
double Pow(int n, int k)
{
if (k > 0)
return n * Pow(n, k - 1);
else if (k == 0)
return 1;
else if (k < 0)
return 1.0 / Pow(n, -k);
}
int main()
{
int n = 0, k = 0;
scanf("%d %d", &n, &k);
double ret = Pow(n, k);
printf("%lf", ret);
return 0;
}
7 计算一个数的每位之和(递归)
//计算一个数的每位之和(递归)
#include <stdio.h>
int DigSum(int n)
{
if (n > 9)
{
return DigSum(n / 10) + n % 10;
}
return n;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = DigSum(n);
printf("%d", ret);
return 0;
}
8 小乐乐走台阶 一步可以走一个或两个,N个台阶有多少种走法
//小乐乐走台阶
#include <stdio.h>
int fib(int n)
{//n=1 1 n=2 2
if (n <= 2)
return n;
else
return fib(n - 1) + fib(n - 2);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("%d", ret);
return 0;
}9 最大公约数
//最大公约数
//方法一:
#include <stdio.h>
int main()
{
int num1 = 0, num2 = 0;
scanf("%d %d", &num1, &num2);
int m = (num1 > num2 ? num1 : num2);
int i = 0;
while (1)
{
if (num1 % m == 0 && num2 % m == 0)
{
break;
}
m--;
}
printf("%d", m);
return 0;
}
//方法二:辗转相除法 最大公约数
#include <stdio.h>
int main()
{
int a = 0, b = 0, c = 0;
scanf("%d %d", &a, &b);
while (c = a % b)
{
a = b;
b = c;
}
printf("%d", b);
return 0;
}
//方法三:函数 辗转相除法
#include <stdio.h>
int divisor(int a, int b)
{
int c = 0;
while (c = a % b)
{
a = b;
b = c;
}
return b;
}
int main()
{
int a = 0, b = 0;
scanf("%d %d", &a, &b);
int ret = divisor(a, b);
printf("%d\n", ret);
return 0;
}
//方法四 递归 辗转相除法
#include <stdio.h>
int divisor(int a, int b)
{
int c = 0;
if (c = a % b)
{
a = b;
b = c;
return divisor(a, b);
}
return b;
}
int main()
{
int a = 0, b = 0;
scanf("%d %d", &a, &b);
int ret = divisor(a, b);
printf("%d\n", ret);
return 0;
}10.递归求1+2+3+4+5+...+10
#include <stdio.h>
int sum(int n)
{
if (n > 1)
return n + sum(n - 1);
else
return 1;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = sum(n);
printf("%d\n", ret);
return 0;
}递归经典问题
1.汉诺塔问题
汉诺塔是根据一个传说形成的数学问题: 有三根杆子A,B,C。A杆上有N 个 穿孔圆盘,盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C 杆: 每次只能移动一个圆盘; 大盘不能叠在小盘上面。 提示:可将圆盘临时置于B 杆,也可将从A 杆移出的圆盘重新移回A 杆,但都必须遵循上述两条规则。 问:如何移?
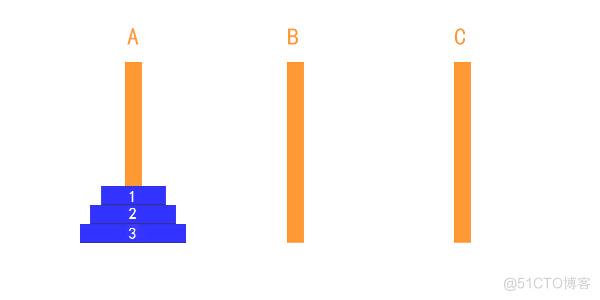
复杂问题的分析,采用递归思想大事化小先分析简单的情况:
1个盘子 移动过程:A->C 1次
2 个盘子 移动过程:A->B A->C B->C 3次
3个盘子 移动过程:A->C A->B C->B A->C B->A B->C A->C 7次
通过总结归纳可以得出:
N个盘子 移动2N-1次
N个盘子移动过程的实现思路:
- 先从A挪动n-1个到B上
- 再将最后的一个从A挪到C上
- 再将B上n-1个盘子借助A挪动到C
void move(char pos1, char pos2)
//起始位置pos1 目标位置pos2
{
printf("%c->%c ", pos1, pos2);
}
void hanoi(int n, char pos1, char pos2, char pos3)
{
if (n == 1)
move(pos1, pos3);
else
{
hanoi(n - 1, pos1, pos3, pos2);//n-1个盘子从pos1(起始)借助pos3(中转)移动到pos2(目标)
move(pos1, pos3);//还剩一个从pos1起始位置挪到pos3目标位置
hanoi(n - 1, pos2, pos1, pos3);//n-1个盘子从pos2(起始)借助pos3(中转)移动到pos2(目标)
}
}
int main()
{
int n = 0;
scanf("%d", &n);//圆盘个数
char pos1 = 'A', pos2 = 'B', pos3 = 'C';
//起始位置pos1 中转位置pos2 目标位置pos3
//从起始到目标要借助中转位置
hanoi(n, pos1, pos2, pos3);
return 0;
}输出:

递归执行过程的理解:多路递归


注意:
- 递归的特点:每次递归时,当前函数只执行一部分,就执行其他部分;在归的过程中会继续执行当前函数的剩下部分;递的次数等于归的次数。
- 函数栈帧角度理解递归:函数没有调用完就不会销毁函数栈帧,函数栈帧创建顺序与递的过程一致,依次创建n=3,n=2,n=1时的函数栈帧,销毁顺序与归的过程一致,按n=1,n=2,n=3顺序销毁,与创建函数栈帧顺序相反。
- 二叉树天生用递归生成的;单路递归eg n!, 多路递归eg fib(n)。
2.青蛙跳台阶问题
动态规划: 大事化小
动态规划的特点:记忆存储值(存储子问题的解) 避免重复计算(所有子问题只需要解决一次)
青蛙跳台阶也可以用动态规划求解,当然这里仅采用递归算法求解
1.一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法(先后次序不同算不同的结果)
采用递归的大事化小思想,先想简单的:
n=1 1 1种跳法
n=2 1,1 2 2种跳法
n=3 1,1,1 1,2 2,1 3种跳法
n阶台阶无非就两种情况:第一步跳一个台阶,还有n-1个台阶;第一步跳两个台阶,还有n-2个台阶 假设f(n)为n阶台阶的跳法,f(1)=1,f(2)=2,f(3)=f(2)+f(1)=3,f(10)=f(9)+f(8) 即f(n)=f(n-1)+f(n-2)
我们就可以根据这个递推出来的公式实现递归
#include <stdio.h>
int f(int n)
{
if (n > 2)
return f(n - 1) + f(n - 2);//fib
else
return n;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = f(n);
printf("%d\n", ret);
return 0;
}2.一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶(n为正整数)总共有多少种跳法。
采用递归的大事化小思想,先想简单的:
n=1 1 1种跳法
n=2 1,1 2 2种跳法
n=3 1,1,1 1,2 2,1 3 4种跳法
n=4 ,分四种情况:第一步跳1级,剩余3级台阶;第一步跳2级,剩余2级台阶;第一步跳3级,剩余1级台阶;第一步跳4级,全部跳完。假设f(n)为n阶台阶的跳法 即f(4)=f(3)+f(2)+f(1)+f(0)

n阶台阶 f(n)=f(n-1)+f(n-2)+f(n-3)+……+f(3)+f(2)+f(1)+f(0) (中间具体项用省略号,不确定的项,无法编程实现继续推导可行的公式)
n-1阶台阶 f(n-1)=f(n-2)+f(n-3)+……+f(3)+f(2)+f(1)+f(0)
====>f(n)=f(n-1)+f(n-1)=2*f(n-1)
#include<stdio.h>
int f(int n)
{
if (n > 1)
return 2 * f(n - 1);
else
return 1;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = f(n);
printf("%d\n", ret);
return 0;
}其他思路:跳上n阶台阶,前面n-1个台阶有两种情况:跳上去/不跳上去 第n个台阶只有一种情况:跳上去(题目要求的必须跳上去) 进行排列组合可得:
f(n)=2n-1种跳法(n>0)
【文章转自 建湖网站开发 http://www.1234xp.com/jianhu.html 欢迎留下您的宝贵建议】