算法练习-day13

二叉树

112. 路径总和

题意：给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。叶子节点 是指没有子节点的节点。

示例：

      思路：本题的思路，我们先排除空树的情况，然后让我们的目标数统一减去根节点的值，之后确定我们递归函数的返回值，我们需要使用bool类型的返回值来返回该路线是否等于targetSum，如果相等，我们返回true，否则就返回false，继续寻找下一条路线；然后对于每条线路值得处理，我们使用模拟回溯的方法，对该路径的目标值进行减的操作

C++代码：

bool CountNode(TreeNode* root,int targetSum)
    {
        if(nullptr==root->left&&nullptr==root->right)//到叶子节点的情况，判断是否该路径等于targetSum
        {
           if(targetSum==0)
           {
               return true;
           }
           return false;
        }
        if(root->left)//模拟实现回溯算法
        {
            targetSum-=root->left->val;
            if(CountNode(root->left,targetSum))
            {
                return true;
            }
            targetSum+=root->left->val;
        }
        if(root->right)
        {
            targetSum-=root->right->val;
            if(CountNode(root->right,targetSum))
            {
                return true;
            }
            targetSum+=root->right->val;
        }
        return false;
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(nullptr==root)//排除空树情况
        {
            return false;
        }
        return CountNode(root,targetSum-root->val);//先删除头节点元素，因为每条路线必须删除头节点
    }

513. 找树左下角的值

题意：给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。假设二叉树中至少有一个节点。

示例：

思路：我们先要确定返回值需要满足的条件：

1. 最底层，最深
2. 最左侧

因此，我们最终的结果可能不是最左侧的，但一定是最深的，因此我们需要定义两个全局变量，一个是现在最左侧的节点值，另一个就是现在最深高度，我们需要满足以上两点，才能输出该值；其次就是模拟回溯算法，保证depth为最深

C++代码：

    int Num=0;
    int MaxDep=INT_MIN;
    void DepthNode(TreeNode* root,int depth)
    {
        if(nullptr==root->left&&nullptr==root->right)
        {
            if(depth>MaxDep)//我们返回的Num必须是最深且最左侧是节点值
            {
                MaxDep=depth;
                Num=root->val;
            }
            return;
        }
        if(root->left)//模拟回溯算法
        {
            depth++;
            DepthNode(root->left,depth);
            depth--;
        }
        if(root->right)
        {
            depth++;
            DepthNode(root->right,depth);
            depth--;
        }
    }
    int findBottomLeftValue(TreeNode* root) {
        DepthNode(root,1);
        return Num;
    }

106. 从中序与后序遍历序列构造二叉树

题意：给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例：

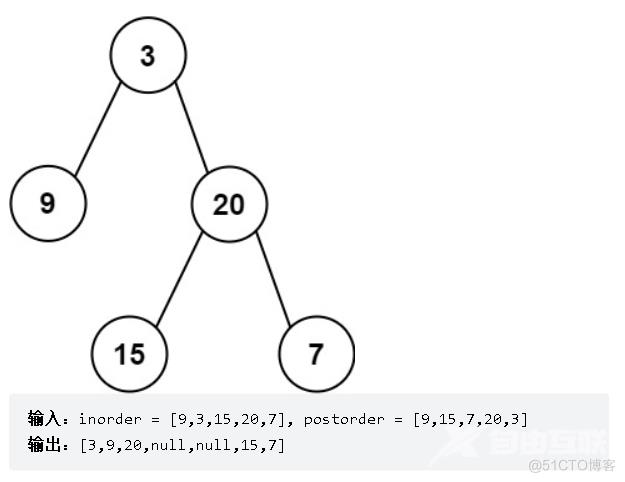
       思路：本题我们可以根据中序遍历数组和后序遍历数组的特点来构建二叉树，首先，后序遍历数组的最后一个元素就是一棵树的根节点，我们就以一棵树的根节点建立二叉树，其次中序遍历可以分割以root为根节点的左右子树节点，我们通过后序遍历，不断分割中序遍历数组

C++代码：

    TreeNode* CreateTree(vector<int>& inorder,vector<int>& postorder)
    {
        if(postorder.size()==0)
        {
            return nullptr;
        }
        int midval=postorder[postorder.size()-1];
        TreeNode* root=new TreeNode(midval);
        int mid=0;
        for(;mid<inorder.size();mid++){//找到中序遍历的中间节点，分离二叉树
            if(inorder[mid]==midval)
            {
                break;
            }
        }
        vector<int> leftinorder(inorder.begin(),inorder.begin()+mid);//切割中序遍历
        vector<int> rightinorder(inorder.begin()+mid+1,inorder.end());
        postorder.resize(postorder.size()-1);//后序遍历的最后一个元素不要，已经作为根节点加入二叉树了
        //切割后序遍历
        vector<int> leftpostorder(postorder.begin(),postorder.begin()+leftinorder.size());
        vector<int> rightpostorder(postorder.begin()+leftinorder.size(),postorder.end());

        root->left=CreateTree(leftinorder,leftpostorder);//左二叉树连接
        root->right=CreateTree(rightinorder,rightpostorder);//右二叉树连接
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return CreateTree(inorder,postorder);
    }