当前位置 : 主页 > 编程语言 > c语言 >

【数据结构】二叉树的实现

来源：互联网 收集：自由互联 发布时间：2023-09-03
一、二叉树我们需要实现的功能 typedef char BTDataType;typedef struct BinaryTreeNode{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;}BTNode;// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉


一、二叉树我们需要实现的功能

typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);

【数据结构】二叉树的实现_二叉树

二、以下为具体功能的实现

        1.创建新节点

                    该步骤创建一个新节点

typedef char BTDataType;

typedef struct BinaryTree
{
    BTDataType data;
    struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

        2.构建二叉树

                        通过数组构建二叉树

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);

        

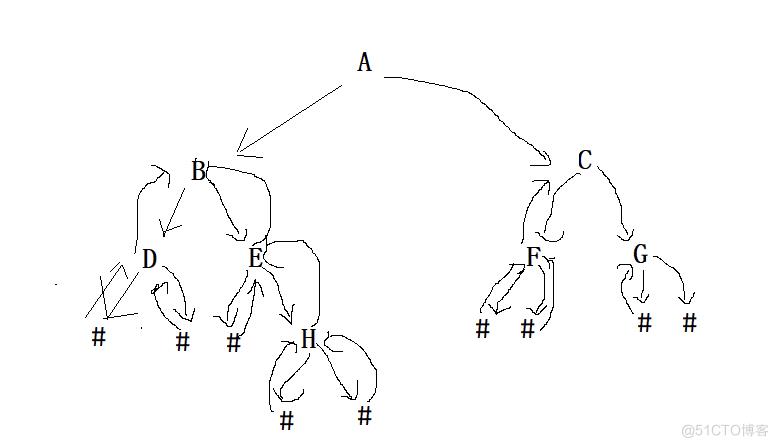
【数据结构】二叉树的实现_#include_02

【数据结构】二叉树的实现_二叉树_03

                 前序遍历：先遍历根，再遍历左子树和右子树

                        注:该步骤：当数组内容为#或者数组已经访问完，都应该返回NULL,当该数组中的内容不为‘#并且数组并未执行完毕，则开辟一块新的空间，类型为BTNode，此时根节点的数据为数组中的内容，并对其进行后置访问，根节点的左节点和根节点的右节点，分别进行遍历，最后我们返回根节点

BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
	if (a[*pi] == NULL || (*pi) >= n)
	{
		a[(*pi)++];
		return NULL;
	}
	
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	if (root == NULL)
	{
		perror("fail:malloc");
		return;
	}
	root->data = a[(*pi)++];
	root->left = BinaryTreeCreate(a,n,pi);
	root->right = BinaryTreeCreate(a,n,pi);
	
	return root;
}

        3、二叉树的销毁

                注：当根节点为空时，我们对其直接进行放回，如果根节点不为空，我们对其进行遍历，访问到最后一个节点，我们对其返回释放

void BinaryTreeDestory(BTNode* root)
{
    if (root == NULL)
		return;

	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	//printf("%p %c\n", root, root->data);
	free(root);
}

        4.二叉树节点个数和二叉树叶子节点的个数

                注：二叉树节点个数，如果根节点为空，则返回0，若根节点不为空我们，对其左右子树进行遍历，并且其往回进行遍历时，我们进行+1操作，最后的返回值即为二叉树节点的个数

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	
	if (root == NULL)
	{
		return 0;
	}
	return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL&&root->right)
	{
		return 1;
	}

}

二叉树的遍历

                在之前我已经写过相关内容的博客，可以点击上面链接直接进行查看

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
		return;

	printf("%c ", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
		return;

	BinaryTreePrevOrder(root->left);
	printf("%c ", root->data);
	BinaryTreePrevOrder(root->right);
}

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
		return;

	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
	printf("%c ", root->data);
}

【数据结构】二叉树的实现_数组_04

        6. 二叉树查找值为x的节点

                注：查找第k层，我们将我们的问题化为小问题，也就是我们第一层的结点需要往下找k-1层，第二层的结点需要往下找k-2层，以此类推，只有当我们的k为1的时候返回的就是我们需要找的k层的结点的个数的总和

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;

	if (root->data == x)
		return root;


	BTNode* ret1 = BinaryTreeFind(root->left, x);
	if (ret1)
		return ret1;

	BTNode* ret2 = BinaryTreeFind(root->right, x);
	if (ret2)
		return ret2;

	return NULL;
}

        7.层序遍历

                注：此时我们采用非递归的方式进行实现，主要用到了队列， 我们清楚队列，是先进先出的方式，我们将数据存储进队列当中，再对其进行取出

      Queue.h

             

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

//前置声明
struct BinaryTreeNode;

typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;

typedef struct
{
	QNode* head;
	QNode* tail;
}Queue;

//初始化
void QueueInit(Queue* pq);

//销毁
void QueueDestroy(Queue* pq);

//放数据
void QueuePush(Queue* pq, QDataType x);

//删除
void QueuePop(Queue* pq);

//长度
int QueueSize(Queue* pq);

//取头
QDataType QueueFront(Queue* pq);

//取尾
QDataType QueueBack(Queue* pq);

//判断空
bool QueueEmpty(Queue* pq);

      Queue.c

#include"queue.h"

//初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
}

//销毁
void QueueDestroy(Queue* pq)
{

	assert(pq);
	QNode* cur = pq->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}

	pq->head = pq->tail = NULL;

}

//放数据
void QueuePush(Queue* pq, QDataType x)
{

	assert(pq);
	//开辟空间
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	//添加数据
	newnode->data = x;
	newnode->next = NULL;

	//链接
	if (pq->tail == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}

}

//判断空
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL;
}

//删除
void QueuePop(Queue* pq)
{

	assert(pq);
	assert(!QueueEmpty(pq));

	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}

}


//取头
QDataType QueueFront(Queue* pq)
{

	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->head->data;
}

//取尾
QDataType QueueBack(Queue* pq)
{

	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->tail->data;
}

//长度
int QueueSize(Queue* pq)
{

	assert(pq);

	QNode* cur = pq->head;
	int count = 0;
	while (cur)
	{
		++count;
		cur = cur->next;
	}

	return count;
}

【数据结构】二叉树的实现_数组_05

     层序遍历的实现

               注：先创建一个队列，对其进行初始化，如果根节点不为空，我们将其放入新创建的队列当中，我们将队列进行循环处理，取出队列当中的首元素，对其进行打印，并销毁，再对二叉树进行递归放入队列当中，如果根节点的左子树中存在数据，我们将其取出放入队列中，如果二叉树的根节点的右子树中，包含数据，我们也对其进行取出放入队列当中，再对队列，进行首元素提取，打印，打印完之后再对该元素进行销毁

void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}

	//如果队列不为空，进入。
	while (!QueueEmpty(&q))
	{
		//取出 打印 
		BTNode* front = QueueFront(&q);
		printf("%c ", front->data);
		QueuePop(&q);

		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}

	}

	printf("\n");
	//销毁队列
	QueueDestroy(&q);
}

【数据结构】二叉树的实现_数组_06

          8.判断是否为完全二叉树

1.如果后面全是空，则是完全二叉树；
2.如果后面还有非空，则不是完全二叉树。

int BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front)
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
		else
		{
			//遇到NULL，跳出。
			break;
		}

	}

	//1.如果后面全是空，则是完全二叉树；
	//2.如果后面还有非空，则不是完全二叉树。
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front)
		{
			QueueDestroy(&q);
			return false;
		}

	}

	QueueDestroy(&q);
	return true;
}

【数据结构】二叉树的实现_二叉树_07

代码汇总：

        bt.h

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<string.h>


typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;


// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);

【数据结构】二叉树的实现_#include_08

bt.c

        

#include"bt.h"
#include"queue.h"

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树


BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
	if (a[*pi] == NULL || (*pi) >= n)
	{
		a[(*pi)++];
		return NULL;
	}
	
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	if (root == NULL)
	{
		perror("fail:malloc");
		return;
	}
	root->data = a[(*pi)++];
	root->left = BinaryTreeCreate(a,n,pi);
	root->right = BinaryTreeCreate(a,n,pi);
	
	return root;
}

// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);
}

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;

	return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;

	if (root->left == NULL && root->right)
		return 1;

	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(k >= 1);
	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;

	if (root->data == x)
		return root;


	BTNode* ret1 = BinaryTreeFind(root->left, x);
	if (ret1)
		return ret1;

	BTNode* ret2 = BinaryTreeFind(root->right, x);
	if (ret2)
		return ret2;

	return NULL;
}

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
		return;

	printf("%c ", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
		return;

	BinaryTreePrevOrder(root->left);
	printf("%c ", root->data);
	BinaryTreePrevOrder(root->right);
}

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
		return;

	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
	printf("%c ", root->data);
}

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root != NULL)
	{
		//如果根节点不为空，我们对其进行存储
		QueuePush(&q,root);
	}
	while (!QueueEmpty(&q))
	{
		//取出 打印
		BTNode* front = QueueFront(&q);
		printf("%c",front->data);
		QueuePop(&q);

		if (front->left)
		{
			QueuePush(&q,front->left);
		}
		if (front->right)
		{
			QueuePush(&q,front->right);
		}
	}
	printf("\n");
	QueueDestroy(&q);

}

// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front)
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
		else
		{
			//遇到NULL，跳出。
			break;
		}

	}

	//1.如果后面全是空，则是完全二叉树；
	//2.如果后面还有非空，则不是完全二叉树。
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front)
		{
			QueueDestroy(&q);
			return false;
		}

	}

	QueueDestroy(&q);
	return true;
}

【数据结构】二叉树的实现_二叉树_09

Queue.h

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

//前置声明
struct BinaryTreeNode;

typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;

typedef struct
{
	QNode* head;
	QNode* tail;
}Queue;

//初始化
void QueueInit(Queue* pq);

//销毁
void QueueDestroy(Queue* pq);

//放数据
void QueuePush(Queue* pq, QDataType x);

//删除
void QueuePop(Queue* pq);

//长度
int QueueSize(Queue* pq);

//取头
QDataType QueueFront(Queue* pq);

//取尾
QDataType QueueBack(Queue* pq);

//判断空
bool QueueEmpty(Queue* pq);

【数据结构】二叉树的实现_数组_10

Queue.c

#include"queue.h"

//初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
}

//销毁
void QueueDestroy(Queue* pq)
{

	assert(pq);
	QNode* cur = pq->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}

	pq->head = pq->tail = NULL;

}

//放数据
void QueuePush(Queue* pq, QDataType x)
{

	assert(pq);
	//开辟空间
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	//添加数据
	newnode->data = x;
	newnode->next = NULL;

	//链接
	if (pq->tail == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}

}

//判断空
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL;
}

//删除
void QueuePop(Queue* pq)
{

	assert(pq);
	assert(!QueueEmpty(pq));

	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}

}


//取头
QDataType QueueFront(Queue* pq)
{

	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->head->data;
}

//取尾
QDataType QueueBack(Queue* pq)
{

	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->tail->data;
}

//长度
int QueueSize(Queue* pq)
{

	assert(pq);

	QNode* cur = pq->head;
	int count = 0;
	while (cur)
	{
		++count;
		cur = cur->next;
	}

	return count;
}

【数据结构】二叉树的实现_二叉树_11

Test.c

#include"bt.h"
#include"queue.h"

int main()
{
    char ch[] = "ABD##E#H##CF##G##";
    //gets(ch);
    int n = strlen(ch);
    int i = 0;
    //BinaryTreeCreate
    BTNode* root = BinaryTreeCreate(ch, n, &i);
    //进行前序遍历，输出遍历结果。
    BinaryTreePrevOrder(root);
    printf("\n");
    //进行中序遍历，输出遍历结果。
    BinaryTreeInOrder(root);
    printf("\n");
    //进行后序遍历，输出遍历结果。
    BinaryTreePostOrder(root);
    printf("\n");
    //结点个数
    int ret = BinaryTreeSize(root);
    printf("%d\n", ret);
    //叶结点的个数
    int ret1 = BinaryTreeLeafSize(root);
    printf("%d\n", ret1);
    //第k个结点
    int ret2 = BinaryTreeLevelKSize(root, 2);
    printf("%d\n", ret2);

    //借用队列实现层序遍历
    BinaryTreeLevelOrder(root);

    // 判断二叉树是否是完全二叉树
    int ret3 = BinaryTreeComplete(root);
    printf("%d\n", ret3);

    BTNode* c = BinaryTreeFind(root, ch[2]);
    printf("%c", c->data);

    BinaryTreeDestory(root);
    root = NULL;
    return 0;
}

【数据结构】二叉树的实现_二叉树_12



上一篇：【数据结构】双向链表的实现
下一篇：没有了
网友评论
相关栏目
最近更新
热门文章