为什么要研究线索二叉树?
当我们用二叉链表作为二叉树的存储结构时,可以很方便地找到某个结点的左右孩子;但一般情况下,无法直接找到该结点在某种遍历序列中的前驱和后继结点。

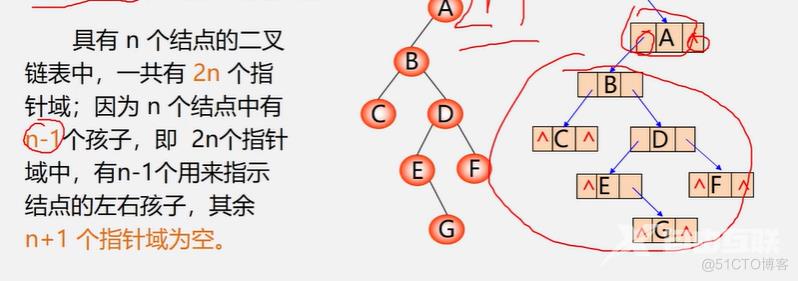
利用二叉链表中的空指针域:
如果某个结点的左孩子为空,则将空的左孩子指针域改为指向其前驱;如果某结点的右孩子为空,则将空的右孩子指针域改为指向其后继。
——这种改变指向的指针称为线索,加上了线索的二叉树称为线索二叉树(Threaded Binary Tree)。
对二叉树按某种遍历次序使其变为线索二叉树的过程叫线索化。
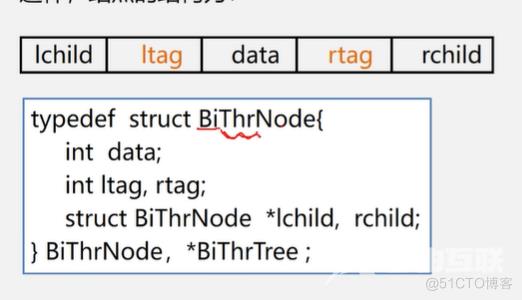
为区分lchild和rchild指针到底是指向孩子的指针,还是指向前驱或者后继的指针,对二叉链表中每个结点增设两个标志域LTag和RTag,并约定:
LTag=0,lchild指向该结点的左孩子;
LTag=1,lchild指向该结点的前驱;
RTag=0,rchild指向该结点的右孩子;
RTag=1,rchild指向该结点的后继。
线索二叉树的目的,是为了直观的表示出某结点的前驱和后继。如果每个结点的前驱或后继都能确定,则对二叉树的遍历就会变得非常简单,一条循环语句即可完成:
for (p=First(T);p!=NULL;p=succ(p))
Visit(p);
二叉链表中,直观的表示出了某结点左右孩子的信息。为了将前驱和后继的信息也表示出来,做如下的规定:
若某结点左指针为空,则令其指向其前驱;若某结点右指针为空,则令其指向其后继。
为区分出是左右孩子还是前驱后继,或者说,为区分出是指针还是线索,结点改变为5个域:除原来的data和lchild、rchild外,再增加ltag(左标志)和rtag(右标志)。并规定ltag=0,指向左孩子;ltag=1,指向前驱。rtag=0,指向右孩子,rtag=1,指向后继。
在线索树上进行遍历,只要先找到序列中的第一个结点,然后依次找结点后继直到后继为空为止。
typedef enum PointerThr
{
Link,Thread
}PointerThr;//Link==0:指针,Thread==1:线索
typedef struct BiThrNode
{
TElemType data;
struct BiThrNode *lchild,*rchild;
PointerThr LTag,RTag;
}BiThrNode,*BiThrTree;手动模拟线索二叉树(中序)
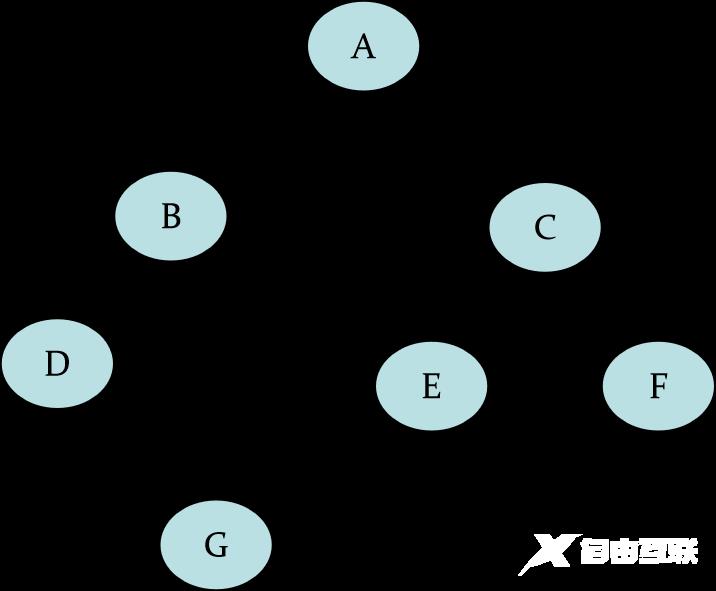
中序遍历为DGBAECF
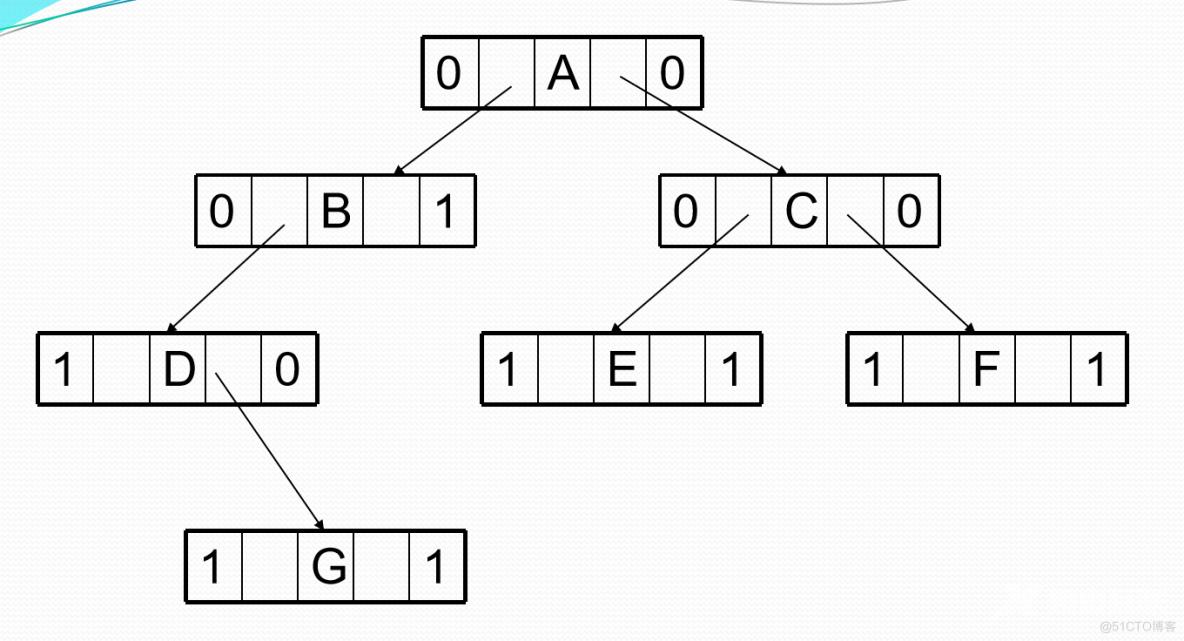
增设一个头结点:
LTag=0,lchild指向根结点,RTag=1,rchild指向遍历序列中最后一个结点,遍历序列中第一个结点的lc域和最后一个结点的rc域都指向头结点。
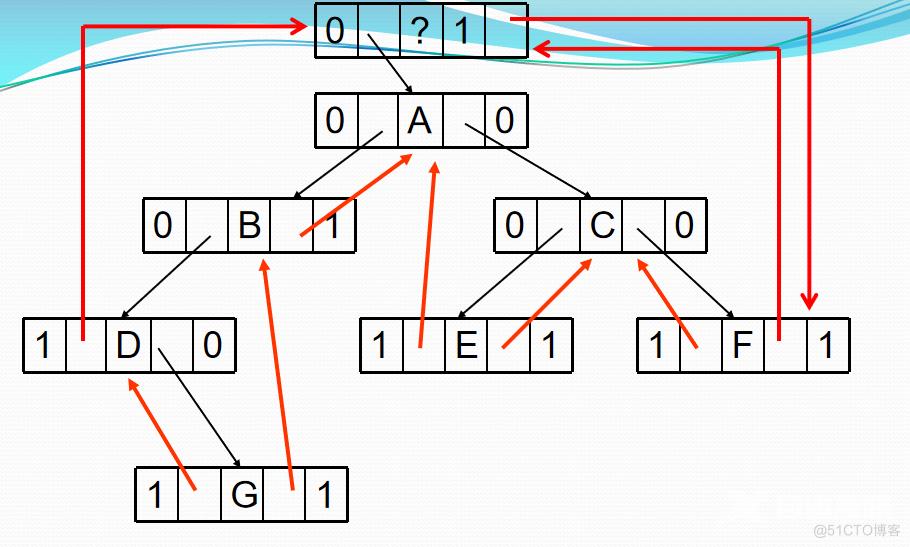
建立中序的线索链表
中序线索化的过程,其实就是在中序遍历的过程中修改空的指针域。问题的关键就是设置另外的一个指针pre,使其始终指向当前结点,或者说p所指向结点的前驱。这样,当p的左指针为空时,将其值修改为pre;而当pre所指的右指针为空时,将其值修改为p即可。
算法设计:中序线索化
中序遍历线索化的递归函数如下:
BiThrTree pre;//全局变量,始终指向刚刚访问过的结点
void InThreading(BiThrTree p)
{
if(p)
{
InThreading(p->lchild);//递归左子树线索化
if(!p->lchild)//没有左孩子
{
p->LTag=Thread;//前驱线索
p->lchild=pre;//左孩子的指针指向前驱
}
if(!pre->rchild)//前驱没有右孩子
{
pre->RTag=Thread;//后继线索
pre->rchild=p;//前驱右孩子指针指向后继
}
pre=p;//保持pre指向p的前驱
InThreading(p->rchild);
}
}if(!p->lchild)表示如果某结点的左指针域为空,因为其前驱结点刚刚访问过,赋值给了pre,所以可以将pre赋值给p->lchild,并修改p->LTag=Thread(也就是定义为1)以完成前驱结点的线索化。
后继比较麻烦,因为此时p结点的后继还没有访问到,因此只能对它的前驱结点pre的右指针做判断,if(!pre->rchild)表示如果为空,则p就是pre的后继,于是pre->rchild=p,并且设置pre->RTag=Thread,完成后继结点的线索化。
完成前驱和后继的判断后,别忘记将当前结点p赋给pre,以便下一次使用。
在二叉树线索链表上添加一个头结点,并令其lchild域的指针指向二叉树的根结点(图中的①),其rchild域的指针指向中序遍历的最后一个结点(图中②)。反之,令二叉树的中序序列中的第一个结点中,lchild域指针和最后一个结点的rchild域指针均指向头结点(图中③和④)。这样定义的好处就是我们既可以从第一个结点起顺后继进行遍历,也可以从最后一个结点起顺前驱进行遍历。
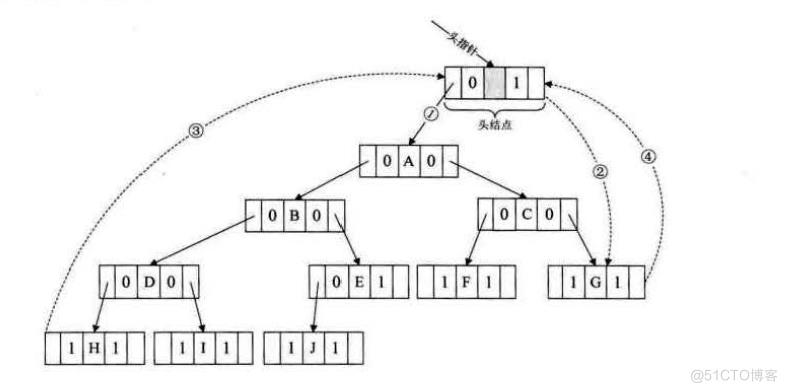
//T指向头结点,头结点左链lchild指向根结点,头结点右链rchild指向中序遍历的最后一个结点
Status InOrderThreading(BiThrTree *Thrt,BiThrTree T)
{
(*Thrt)=(BiThrTree)malloc(sizeof(BiThrNode));
if(!(*Thrt))
exit(OVERFLOW);
(*Thrt)->LTag=Link;//Thrt->LTag=0;
(*Thrt)->RTag=Thread;//Thrt->RTag=1;
(*Thrt)->rchild=*Thrt;
if(!T)
(*Thrt)->lchild=(*Thrt);
else
{
(*Thrt)->lchild=T;
pre=(*Thrt);
//线索化
InThreading(T);
pre->rchild=(*Thrt);
pre->RTag=Thread;
(*Thrt)->rchild=pre;
}
return OK;
}如何找第一个结点
中序序列第一个结点:从根开始,向左走到尽头。
BiThrTree First(BiThrTree p)
{
if(!p)
return NULL;
while(p->LTag==Link)
p=p->lchild;
return p;
}如何找每个结点的后继
若p->RTag为线索,则后继为p->rchild
若p->RTag为指针,说明p有右子树,因中序遍历的顺序为左根右,将p看作根,后继为其右子树中序序列的第一个结点。
向右走一步,再向左走到尽头。
BiThrTree succ(BiThrTree p)
{
if(p->RTag==Thread)
return p->rchild;
p=p->rchild;
while(p->LTag==Link)
p=p->lchild;
return p;
}如何找最后一个结点
中序序列的最后一个结点:从根开始,向右走到尽头
直接取头结点的rchild
BiThrTree Last(BiThrTree Thrt)
{
return Thrt->rchild;
}如何找每个结点的前驱
若p->LTag为线索,则前导为p->lchild
若p->LTag为指针,说明p有左子树,中序遍历的顺序为左根右,将p看作根,前导为其左子树中序序列的最后一个结点。
向左走一步,再向右走到尽头。
BiThrTree prec(BiThrTree p)
{
if(p->LTag==Thread)
return p->lchild;
p=p->lchild;
while(p->RTag==Link)
p=p->rchild;
return p;
}代码实现
#include<stdio.h>
#include<stdlib.h>
#define OVERFLOW -2
#define OK 1
typedef enum PointerTag {Link,Thread} PointerTag;//Link==0,指针 Thread==1,线索
typedef char TElemType;
typedef int Status;
typedef struct BiThrNode
{
TElemType data;
struct BiThrNode *lchild,*rchild;
PointerTag LTag,RTag;
}BiThrNode,*BiThrTree;
BiThrTree pre;
void InThreading(BiThrTree);
Status CreatBiTree(BiThrTree *T)
{
char ch;
ch=getchar();
if(ch=='#')
*T=NULL;
else
{
(*T)=(BiThrNode*)malloc(sizeof(BiThrNode));
if(!*T)
exit(OVERFLOW);
(*T)->data=ch;
(*T)->LTag=Link;
(*T)->RTag=Link;
CreatBiTree(&(*T)->lchild);
CreatBiTree(&(*T)->rchild);
}
return OK;
}
Status InOrderTravese(BiThrTree T,Status (*visit)(TElemType e))
{
if(T)
{
InOrderTravese(T->lchild,visit);
(*visit)(T->data);
InOrderTravese(T->rchild,visit);
}
return OK;
}
Status visit(TElemType e)
{
printf("%c\t",e);
return OK;
}
Status InOrderThreading(BiThrTree *Thrt,BiThrTree T)
{
(*Thrt)=(BiThrTree)malloc(sizeof(BiThrNode));
if(!(*Thrt))
exit(OVERFLOW);
(*Thrt)->LTag=Link;//Thrt->LTag=0;
(*Thrt)->RTag=Thread;//Thrt->RTag=1;
(*Thrt)->rchild=(*Thrt);
if(!T)
(*Thrt)->lchild=(*Thrt);
else
{
(*Thrt)->lchild=T;
pre=(*Thrt);
//线索化
InThreading(T);
pre->rchild=(*Thrt);
pre->RTag=Thread;
(*Thrt)->rchild=pre;
}
return OK;
}
void InThreading(BiThrTree p)
{
if(p)
{
InThreading(p->lchild);
if(!p->lchild)
{
p->LTag=Thread;
p->lchild=pre;
}
if(!pre->rchild)
{
pre->RTag=Thread;
pre->rchild=p;
}
pre=p;
InThreading(p->rchild);
}
}
BiThrTree First(BiThrTree p)
{
if(!p)
return NULL;
while(p->LTag==Link)
p=p->lchild;
return p;
}
BiThrTree succ(BiThrTree p)
{
if(p->RTag==Thread)
return p->rchild;
p=p->rchild;
while(p->LTag==Link)
p=p->lchild;
return p;
}
BiThrTree prec(BiThrTree p)
{
if(p->LTag==Thread)
return p->lchild;
p=p->lchild;
while(p->RTag==Link)
p=p->rchild;
return p;
}
BiThrTree last(BiThrTree Thrt)
{
return Thrt->rchild;
}
int main()
{
BiThrTree T,Thrt,p;
char ch;
printf("请输入一个二叉链表:");
CreatBiTree(&T);
printf("中序遍历后的二叉链表为:");
InOrderTravese(T,visit);
printf("\n");
printf("中序线索化的二叉链表为:");
InOrderThreading(&Thrt,T);
for(p=First(T);p!=Thrt&&p;p=succ(p))
printf("%c",p->data);
putchar('\n');
return 0;
}
