为什么要研究二叉树?因为普通树(多叉树)若不转化为二叉树,则运算很难实现。
二叉树在树结构的应用中起着非常重要的作用,因为对二叉树的许多操作算法简单,而任何树都可以与二叉树相互转换,这样就解决了树的存储结构及其运算中存在的复杂性。
二叉树的定义
二叉树是由n(n>=0)个结点的有限集合构成,此集合或者为空集,或者由一个根结点及两棵互不相交的左右子树组成,并且左右子树都是二叉树。简单的说:二叉树是一棵特殊的树,只不过其中每个结点最多有两个孩子。
特点:每个结点最多有俩孩子(二叉树中不存在度大于2的结点)。子树有左右之分,其次序不能颠倒。二叉树可以是空集合,根可以有空的左子树或空的右子树。
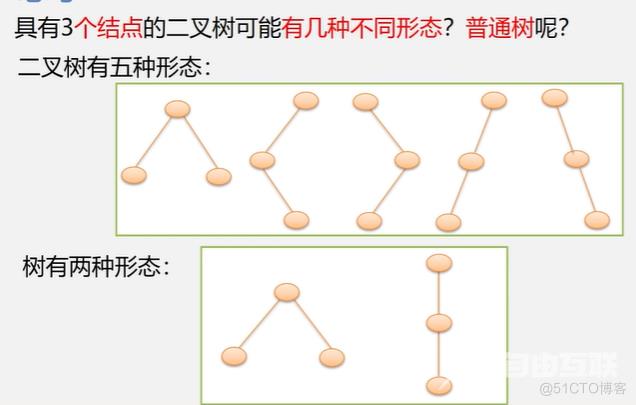
注意:二叉树不是树的特殊情况,它们是两个概念。二叉树每个结点位置或者说次序都是固定的,可以是空,但是不可以说它没有位置,而树的结点位置是相对于别的结点来说的,没有别的结点时,它就无所谓左右了。
树和二叉树的抽象数据类型定义
Assign(T, &e, value); //对二叉树T中结点e赋值
Root(T);
Value(T, e);
Parent (T, e);
LeftChild (T, e);
RightChild (T, e);
LeftSibling (T, e);
RightSibling (T, e);
PreOrderTraverse(T, Visit());
InOrderTraverse(T, Visit());
PostOrderTraverse(T, Visit());
LevelOrderTraverse(T, Visit());
InsertChild(T, p, LR, c);
初始条件:二叉树T存在,p指向T中某结点,LR值为0或1,非空二叉树c与T不相交且右子树为空
操作结果:根据LR为0和1,插入c为p所指结点的左或右子树,p所指结点原有子树成为c的右子树
DeleteChild(T, p, LR);
} ADT BinaryTree二叉树的性质和存储结构
性质1: 在二叉树的第i层上至多有2^(i-1)个结点(i>=1)。
证明:用归纳法证明之
- i=1时,只有一个根结点,命题正确
- 假设i=n-1时命题成立,即第n-1层上的结点个数至多有2n-2个
- i=n时,根据二叉树的定义,第n层上最大结点数是第n-1层的2倍,即2*2n-2=2n-1,命题得证
性质2:深度为k的二叉树至多有2^k-1个结点(k>=1),最少得有k个结点。
性质3: 对任何一棵二叉树,如果其(叶子树)终端结点数为n0,度为2的结点数为n2,则 n0=n2+1。
两种特殊形式的二叉树
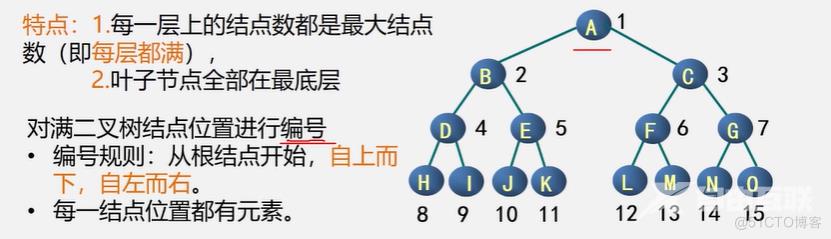
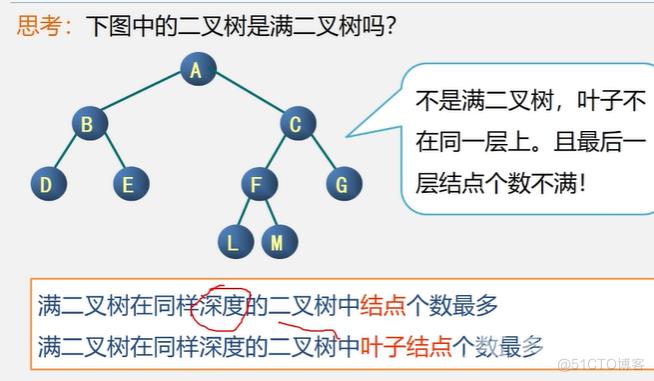
满二叉树:
深度为k,且含有2^k-1个结点的二叉树,即每层结点数均为最大值。
完全二叉树:
深度为k的二叉树,前k-1层结点值达到最大,而第k层只自右向左缺少连续的若干个结点。
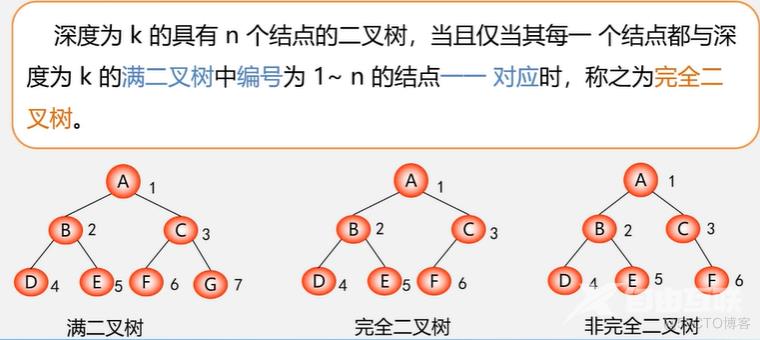
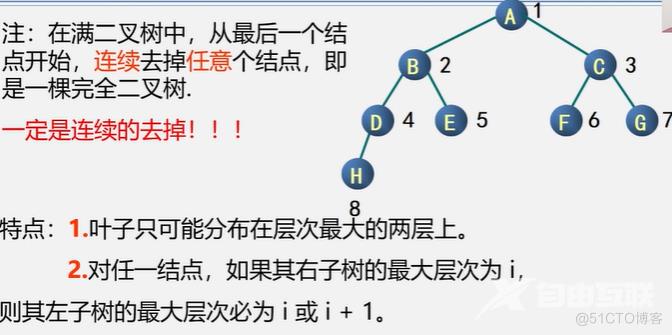
满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。

性质5: 如果对一棵有n个结点的完全二叉树的所有结点按层序编号(自上向下,同层从左到右),则对任一结点i (1<=i<=n),有:
(1)如果i=1,则结点i无双亲,是二叉树的根;如果i>1,则其双亲是结点 i/2
(2)如果2i>n,则结点i为叶子结点,无左孩子;否则,其左孩子是结点2i。 (3)如果2i+1>n,则结点i无右孩子;否则,其右孩子是结点2i+1。
假设一棵完全二叉树有700个结点,则其叶子结点有多少个?
根据性质4,700个结点的完全二叉树为10层
根据性质2,前9层有511个结点,则第10层结点数为189个,均为叶子结点 根据性质1,第9层结点数为256个,其中前95个为第10层189个结点的双亲,因此第9层的叶子数为161个 所以叶子结点总数为189+161=350个
完全二叉树700个结点可以编号为1-700,其中最后一个结点即700号结点的双亲必为350号,且为350号的左孩子。因此350号是树中最后一个拥有孩子的结点,即从351号开始均为叶子,所以叶子总数为350个
二叉树的顺序存储
实现:按满二叉树的结点层次编号,依次存放二叉树中的数据元素
存储方式:用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素,即将完全二叉树上编号为i的结点元素存储在一维数组中下标为i-1的分量中(可以舍弃数组的0号元素不用)
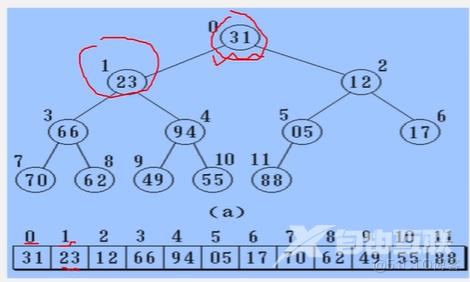
//二叉树顺序存储表示
#define MAXSIZE 100//二叉树的最大结点数
Typedef TElemType SqBiTree[MAXSIZE];//0号单元存储根结点
SqBiTree BT;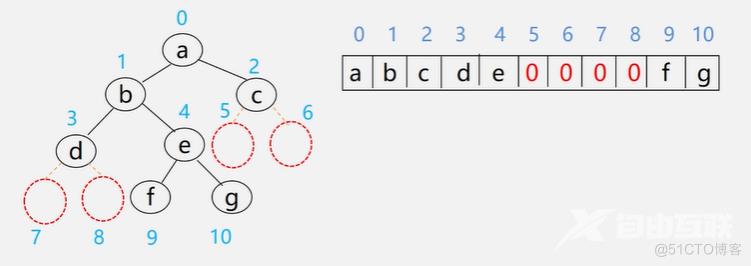
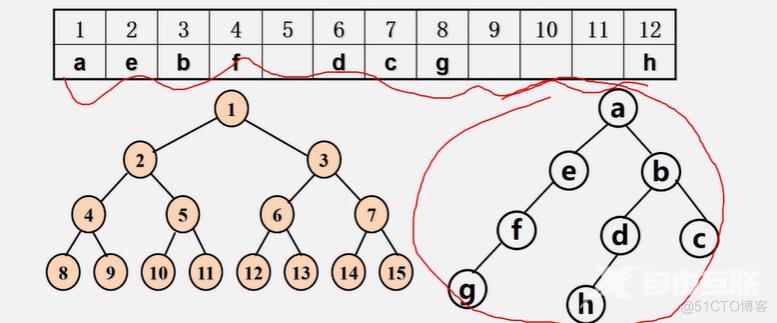
二叉树的顺序存储缺点:
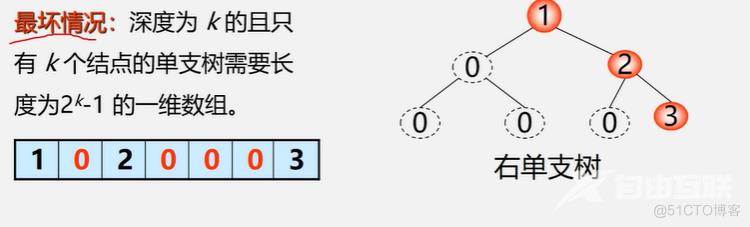
特点:结点间关系蕴含在其存储位置中,浪费空间,只适于存满二叉树和完全二叉树
二叉树的链式存储结构

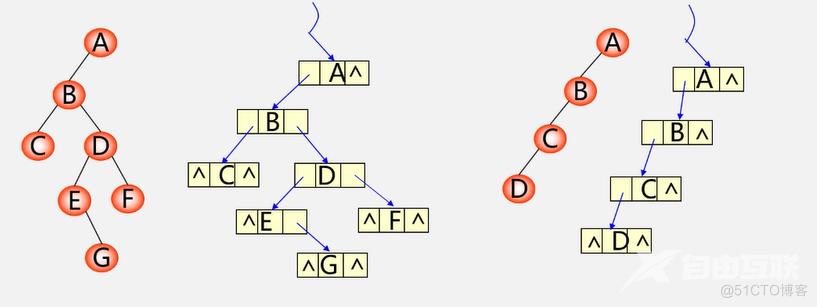
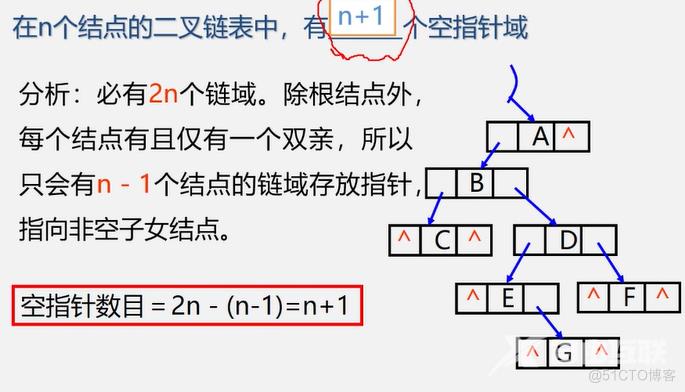
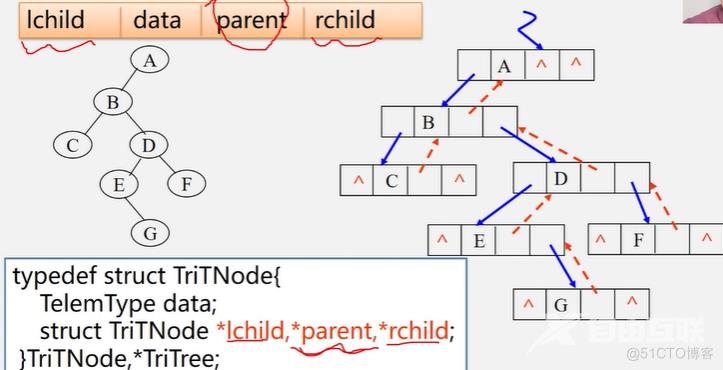
二叉树的遍历
三类遍历方式:先上后下的层次遍历、先左后右的遍历、先右后左的遍历。
对于先左后右的方式,依据访问根的时机,又可分为先根(序)、中根(序)、后根(序)三种遍历方式。


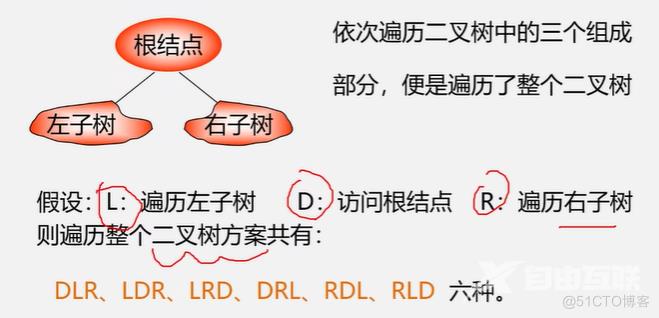

先根遍历
若二叉树为空,则返回;否则
(1)访问根结点;
(2)先序遍历左子树
(3)先序遍历右子树
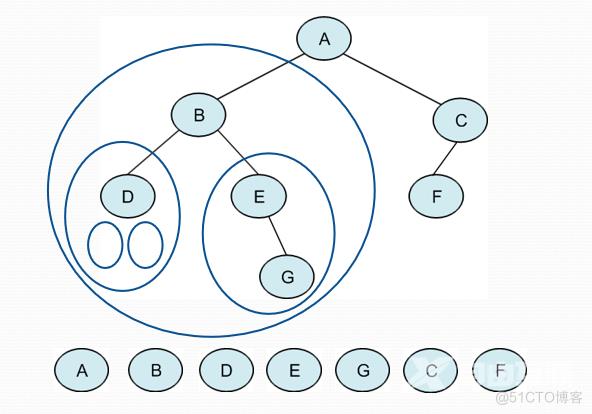
遍历过程:访问A结点,先序遍历B结点,先序遍历D,先序遍历D的左子树为空,结束,先序遍历右子树为空,结束,先序遍历D结束,先序遍历B左子树结束,先序遍历E,先序遍历E左子树为空结束,先序遍历G,先序遍历E结束,先序遍历B结束;先序遍历C,先序遍历C的左子树F,先序遍历F左子树为空结束,先序遍历右子树为空结束,先序遍历F结束,先序遍历C右子树为空结束,先序遍历C结束,先序遍历A结束。
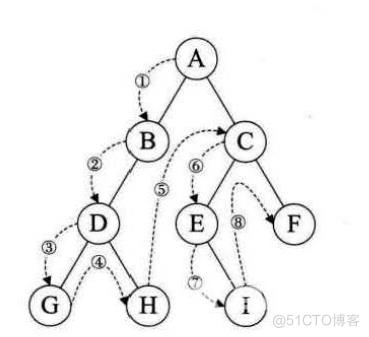
中根遍历
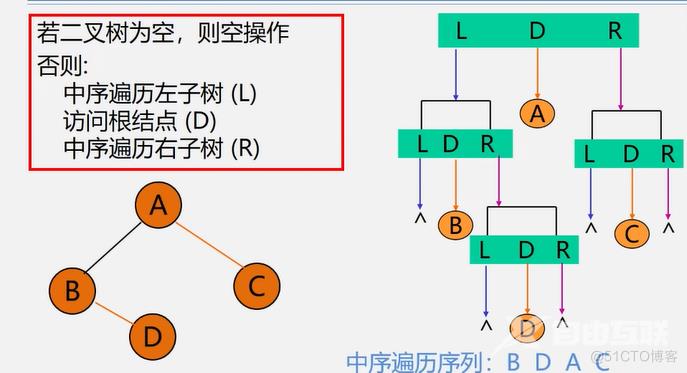
若二叉树为空,则返回;否则
(1)中根遍历左子树;
(2)访问根节点;
(3)中根遍历右子树。
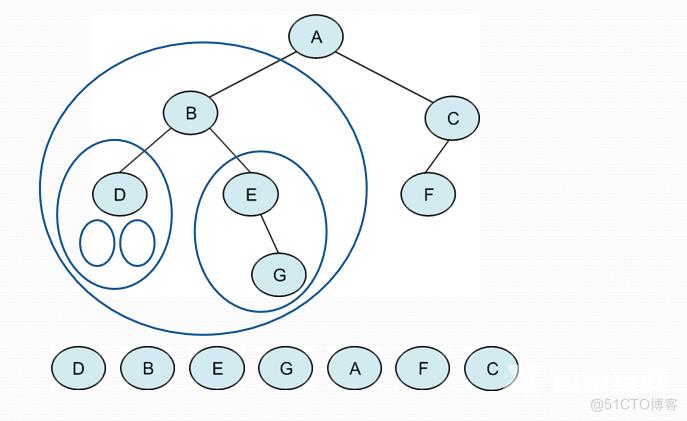
遍历过程:
中序遍历D的左子树为空,遍历D,中序遍历D的右子树为空,结束,中序遍历D结束,中序遍历B,中序遍历E的左子树为空,访问E,中序遍历E的右子树G,中序遍历G的左子树为空结束,访问G,中序遍历G的右子树为空,结束,访问A,中序遍历F,左子树为空,访问F,中序遍历右子树为空结束,访问C,中序遍历C的右子树为空结束,中序遍历结束。
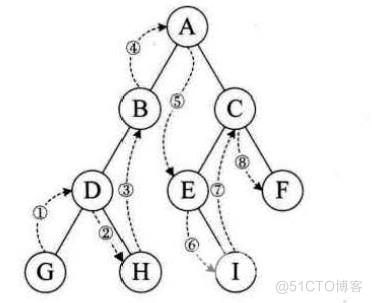
后根遍历
若二叉树为空,则返回;否则
(1)后根遍历左子树;
(2)后根遍历右子树;
(3)访问根节点。
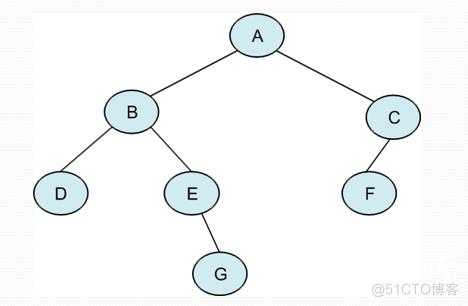
访问顺序为:D G E B F C A

根据遍历序列确定二叉树
若二叉树中各结点的值均不同,则二叉树结点的先序序列、中序序列和后序列都是唯一的。
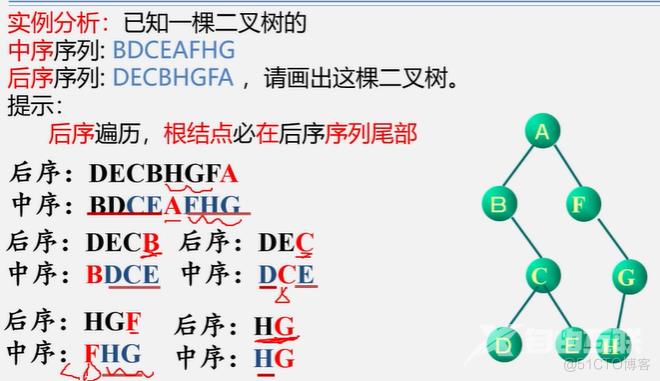
由二叉树的先序序列和中序序列,或由二叉树的后序序列和中序序列可以确定唯一一棵二叉树。
例:已知二叉树的先序和中序序列,构造出相应的二叉树
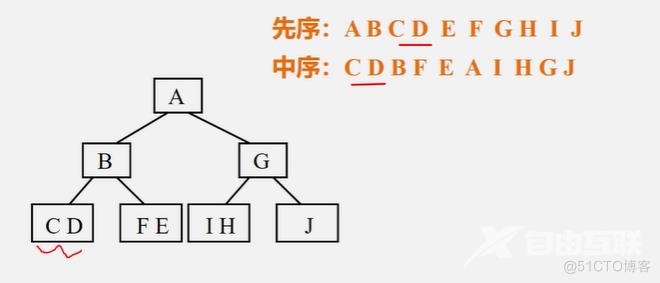
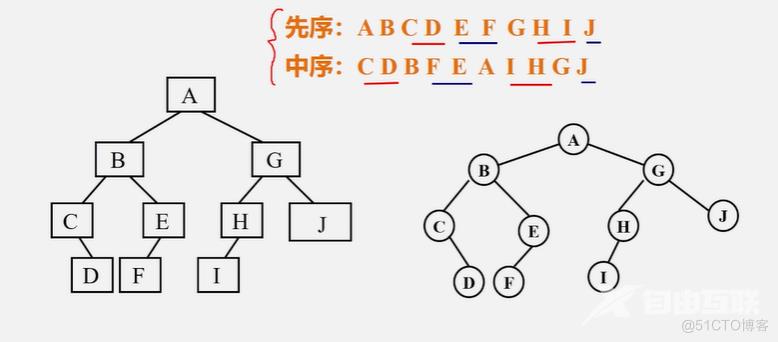
先序:ABCDEFGHIJ
中序:CDBFEAIHGJ
首先能确定A是根,在中序中找到根的话,就能确定左边这些都是在左子树上,右边这些都是在右子树上。由此能确定BCDEF是左子树,GHIJ为右子树,左子树先序一定也是根在前,右子树也是。
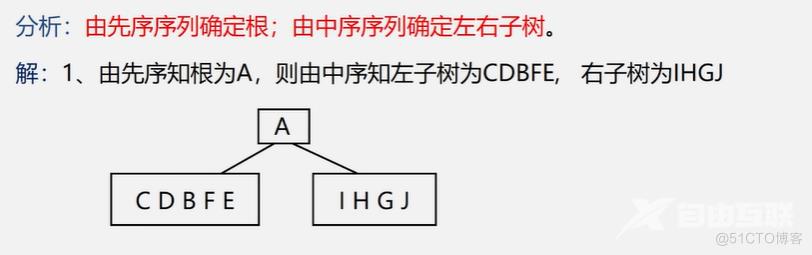
遍历算法的实现——先序遍历
若二叉树为空,则空操作;
若二叉树非空,
访问根结点,前序遍历左子树,前序遍历右子树
Status PreOrderTraverse(BiTree T,Status (*visit)(TElemType e))
{
if(T){
(*visit)(T->data);
PreOrderTraverse(T->lchild,visit);
PreOrderTraverse(T->rchild,visit);
}
else return OK;
}遍历算法的实现——中序遍历
Status InOrderTraverse(BiTree T ,Status (*visit)(TElemType e)){
if(T){
InOrderTraverse(T->lchild,visit);
(*visit)(T->data);
InOrderTraverse(T->rchild,visit);
}
else return OK;
}遍历算法的实现——后序遍历
若二叉树为空,则空操作;
若二叉树非空,
后序遍历左子树,前序遍历右子树,访问根结点。
Status PostOrderTraverse(BiTeer T,Status (*visit)(TElemType e))
{
if(T)
{
PostOrderTraverse(T->lchild,visit);
PostOrderTraverse(T->rchild,visit);
(*visit)(T->data);
}
else
return OK;
}如果去掉输出语句,从递归的角度来看,三种算法是完全相同的,或说这三种算法的访问路径是相同的,只是访问结点的时机不同。
时间效率:O(n),每个结点只访问一次
空间效率:O(n),栈占用的最大辅助空间
代码实现
#include<stdio.h>
#include<stdlib.h>
#define OVERFLOW -2
#define OK 1
#define ERROR 0
typedef int Status;
typedef char TElemType;
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
Status CreateBiTree(BiTree *T)
{
char ch;
ch=getchar();
if(ch=='#')
*T=NULL;
else
{
(*T)=(BiTNode*)malloc(sizeof(BiTNode));
if(!*T)
exit(OVERFLOW);
(*T)->data=ch;
CreateBiTree(&(*T)->lchild);
CreateBiTree(&(*T)->rchild);
}
return OK;
}
Status PreOrderTraverse(BiTree T,Status (*visit)(TElemType e))
{
if(T)
{
(*visit)(T->data);
PreOrderTraverse(T->lchild,visit);
PreOrderTraverse(T->rchild,visit);
}
else
return OK;
}
Status InOrderTraverse(BiTree T,Status (*visit)(TElemType e))
{
if(T)
{
InOrderTraverse(T->lchild,visit);
(*visit)(T->data);
InOrderTraverse(T->rchild,visit);
}
else
return OK;
}
Status PostOrderTraverse(BiTree T,Status (*visit)(TElemType e))
{
if(T)
{
PostOrderTraverse(T->lchild,visit);
PostOrderTraverse(T->rchild,visit);
(*visit)(T->data);
}
else
return OK;
}
Status visit(TElemType e)
{
printf("%c\t",e);
return OK;
}
int main()
{
BiTree T;
char ch;
printf("请输入一个二叉链表:");
CreateBiTree(&T);
printf("先序遍历的二叉链表为:\n");
PreOrderTraverse(T,visit);
printf("\n");
printf("中序遍历的二叉链表为:\n");
InOrderTraverse(T,visit);
printf("\n");
printf("后序遍历的二叉链表为:\n");
PostOrderTraverse(T,visit);
printf("\n");
return 0;
}中序遍历非递归算法
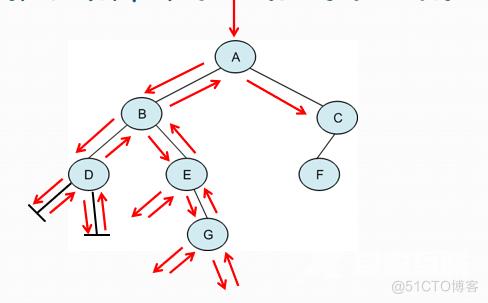
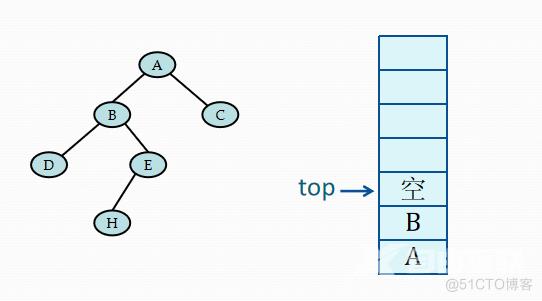
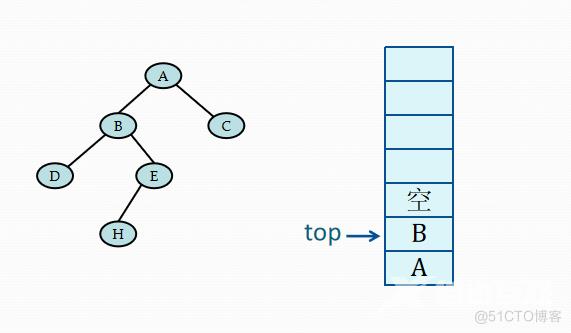
二叉树中序遍历的非递归算法的关键:在中序遍历过某结点的整个左子树之后,如何找到该结点的根以及右子树。
基本思想:
(1)建立一个栈
(2)根结点进栈,遍历左子树
(3)根结点出栈,输出根结点,遍历右子树
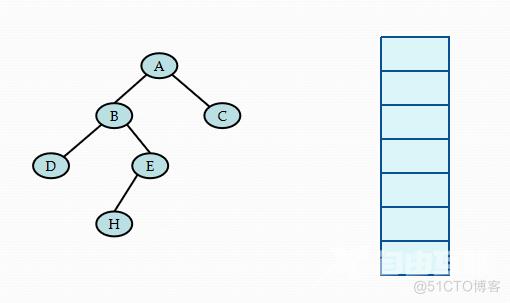
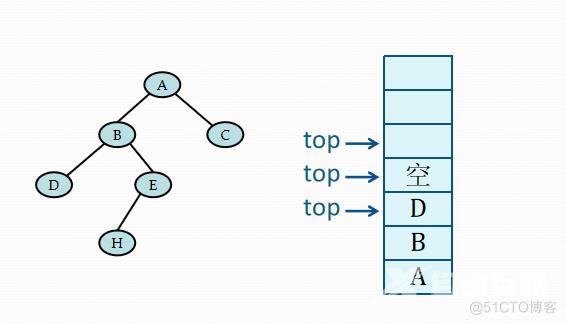
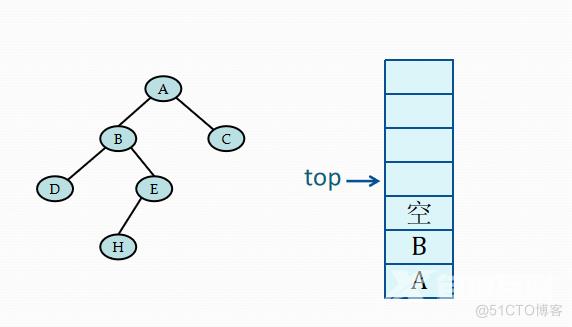
当栈顶记录中的指针非空时,应遍历左子树,即指向左子树根的指针进栈。若栈顶记录中的指针值为空,则应退至上一层,若是从左子树返回,则应访问当前层即栈顶记录中指针所指的根结点。若是从右子树返回,则表明当前层的遍历结束,应继续退栈。从另一角度看,这意味着遍历右子树时不再需要保存当前层的根指针,可直接修改栈顶记录的指针即可。
Status InOrderTraverse(BiTree T,Status (*visit)(TElemType e))
{
InitStack(S);
Push(S,T);//根指针进栈
while(!StackEmpty(S))
{
while(GetTop(S,p)&&p)
Push(S,p->lchild);//向左走到尽头
Pop(S,p);//空指针退栈
if(!StackEmpty(S))
{//访问结点,向右一步
Pop(S,p);
(*visit)(p->data);
Push(S,p->rchild);
}
}
return OK;
}Status InOrderTraverse(BiTree T,Status (*visit)(TElemType e))
{
InitStack(S);
p=T;
while(p||!StackEmpty(S))
{
if(p)
{
Push(S,p);
p=p->lchild;
}//根指针进栈,遍历左子树
else
{
Pop(S,p);
if(!visit(p->data)) return ERROR;
p=p->rchild;
}
}
return OK;
}
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define OK 1
#define OVERFLOW -2
typedef struct BiTNode//二叉树的结构体
{
char data;//二叉树的数据域
struct BiTNode *lchild,*rchild;//二叉树的指针域
}BiTNode ,*BiTree;
typedef struct StackNode //栈的结构体
{
BiTree data;//栈的数据域,(数据域为二叉树的一个结点)
struct StackNode *next; //栈的指针域
}SqStack,*LinkStack;
void InitStack(LinkStack &S)//栈的初始化,只有创建一个栈顶结点这一步
{
S = (SqStack*)malloc(sizeof(SqStack));//创建一个结点,使其为NULL,便成为栈顶结点。
S = NULL;
}
int Push(LinkStack &S,BiTree T)//进栈
{
SqStack* p;//定义一个野结点
p = (SqStack*)malloc(sizeof(SqStack));
p->data = T;//使该结点装上数据元素T,并使其next等于S,类似于链表的头插法
p->next = S;
S = p;//栈顶结点S,一直在栈的最前方
return 0;
}
void Pop(LinkStack &S,BiTree &T)
{
if(S==NULL)//判断栈是否为空
{
printf("栈空!");
}
else
{
SqStack* p;//这里定义一个结点,方便后面对栈顶结点的释放
T = S->data;
p = S;
S = S->next;//使栈顶结点指向下一个结点,类似于栈减一
free(p);//释放栈顶元素
}
}
int CreateBiTree(BiTree *T)
{
char ch;
ch=getchar();
if(ch=='#')
*T=NULL;
else
{
(*T)=(BiTNode*)malloc(sizeof(BiTNode));
if(!*T)
exit(OVERFLOW);
(*T)->data=ch;
CreateBiTree(&(*T)->lchild);
CreateBiTree(&(*T)->rchild);
}
return OK;
}
void InOrderTraverse(BiTree T)//中序遍历二叉树T的非递归算法
{
LinkStack S;
InitStack(S);//创建一个栈,并初始化
BiTree p = T;
while(p || S!=NULL)//循环终止条件是p为NULL与S等于NULL,两个条件同时满足的情况下,循环终止
{
if(p)//p非空
{
Push(S,p);//根指针进栈
p = p->lchild;//遍历左子树
}
else
{
Pop(S,p);//出栈
printf("%c ",p->data);//访问根结点
p = p->rchild;//遍历右子树
}
}
}
int main()
{
BiTree T;
printf("请输入先序遍历的二叉链表:");
CreateBiTree(&T);//创建一个二叉树
printf("先序遍历为:");
InOrderTraverse(T);//非递归中序遍历二叉树
printf("\n");
return 0;
}三个推论

两个定理

定理一证明:
①当n=0时,可以确定二叉树为空,结论正确。
②假设结点数小于n的任何二叉树,均可以由先序和中序序列唯一确定。
③对具有n个结点的二叉树 设其先序序列为:a0a1a2…an-1 中序序列为: b0b1...bk-1bkbk+1…bn-1
因在先序遍历中,首先访问根结点,再遍历左子树,最后遍历右子树,所以a0必为整个二叉树的根结点,而且a0也必然在中序序列中出现,即中序序列中必有一个结点bk(0<=k<=n-1)就是根结点a0
由于bk是根结点,而中序遍历时,首先遍历左子树,再访问根结点,最后遍历右子树。因此在中序序列中b0b1...bk-1必为bk的左子树的中序序列,即bk的左子树有k个结点;bk+1…bn-1必为bk的右子树的中序序列,即右子树有n-k-1个结点。
另外:在先序序列中,紧跟在a0后的k个结点a1...ak必为其左子树的先序序列,ak+1…an-1必为其右子树的先序序列。
根据假设:结点树小于n的二叉树可由先序和中序序列唯一确定
则由子先序序列a1…ak和子中序序列b0…bk-1可以唯一确定a0的左子树 又由子先序序列ak+1…an-1和子中序序列bk+1…bn-1可以唯一确定a0的右子树 综上所述:此树的根及其左右子树均能唯一确定,因此整个二叉树也就唯一确定了。
常见题型:单选、填空、简答
1. 某二叉树的先序遍历和后序遍历的序列正好相反,则该二叉树一定是( D )
A 空树或只有一个结点 B 完全二叉树 C 二叉排序树 D 高度与结点数相同
先序遍历:根左右 后序遍历:左右根
2. 一棵二叉树的先序遍历序列为abcdefg,它的中序遍历序列可能是( B )
A cabdefg B abcdefg C dacefbg D adcbgef
先序遍历:根左右 中序遍历:左根右
当一棵二叉树所有结点的左子树为空时,先序遍历和中序遍历相同
3. 已知二叉树的先序序列为ABDEGCF,中序序列为DBGEACF,则后序序列为DGEBFCA
判断
1. 二叉树的遍历就是为了在应用中找到一种线性的次序 ( T )
- 给定二叉树的某种遍历结果,对应的二叉树不是唯一的 ( T )
- 由一棵二叉树的先序和后序序列可以唯一的确定一棵二叉树 ( F )
简答
1.如果二叉树结点的先序序列、中序序列和后序序列中,结点A、B的位置都是A在前B在后,则A B可能是兄弟么?A可能是B的双亲么?A可能是B的孩子么?
先序序列:根左右 中序序列:左根右 后序序列:左右根
AB可能是兄弟,A不可能是B的双亲,A不可能是B的孩子
2. 一棵二叉树的先序、中序和后序序列分别如下,其中一部分未显示出来。试求出空格处的内容,并画出该树
先序:(A)B(D)F(K)I C E H(J) G
中序: D(B)K F I A(H)E J C (G)
后序:(D)K(I)F B H J (E)G(C)A
典型算法——层次遍历
层次遍历是一种广度优先搜索算法,用于遍历树或图的节点。在C语言的数据结构中,层次遍历通常使用队列实现。
算法思路:使用一个队列
1. 将根结点入队列。
2. 队不空时循环:从队列中出列一个结点*p,访问它;
a. 若它有左孩子结点,将左孩子结点进队;
b. 若它有右孩子结点,将右孩子结点进队。
层次遍历的主要思想是从根节点开始,从上到下一层一层地遍历树的节点,直到遍历到最后一层。在每一层中,节点按照从左到右的顺序访问,每个结点只访问一次。
在算法实现时,因为队列的先进先出特性,保证了以广度优先的方式逐层遍历树的节点。每次弹出队列中的第一个节点并将其子节点入队列,保证了每个节点都会被遍历且仅会被遍历一次,从而实现了层次遍历。
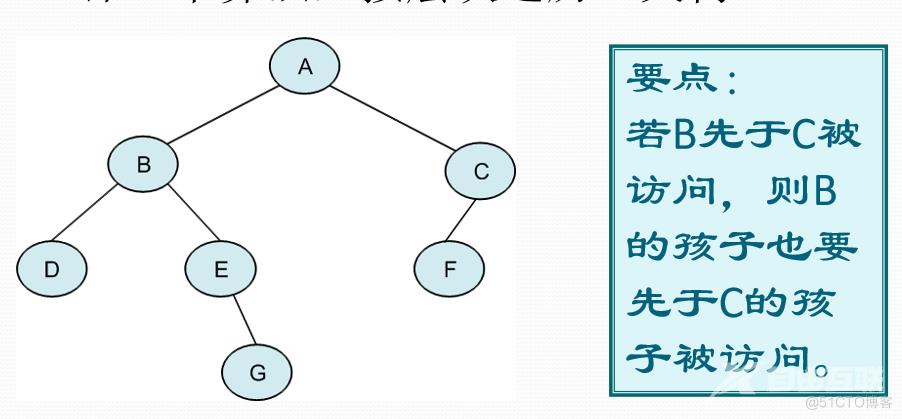
首先根结点A入队,A出队,将A的两个孩子入队,即B C入队,继续将B出队,B的两个孩子入队,即D E入队,将C出队,同时F入队。将D出队,同时孩子入队,无孩子就算了,将E出队,同时G入队。将F出队。将G出队。全部出队完毕。
void LevelOrder(BiTree T)
{
BiTree Q[MAXSIZE],p;
int front,rear;
front=rear=0;
if(!T)
return ;
printf("%c",T->data);
rear++;
Q[rear]=T;
while(rear!=front)
{
front=(front+1)%MAXSIZE;
p=Q[front];
if(p->lchild!=NULL)
{
printf("%c",p->lchild->data);
rear=(rear+1)%MAXSIZE;
Q[rear]=p->lchild;
}
if(p->rchild!=NULL)
{
printf("%c",p->rchild->data);
rear=(rear+1)%MAXSIZE;
Q[rear]=p->rchild;
}
}
}二叉树遍历算法的应用——二叉树的建立
按先序遍历序列建立二叉树的二叉链表

Status CreateBiTree(BiTree *T)
{
char ch;
ch=getchar();
if(ch=='#')
*T=NULL;
else
{
(*T)=(BiTNode*)malloc(sizeof(BiTNode));
if(!*T)
exit(OVERFLOW);
(*T)->data=ch;//生成根结点
CreateBiTree(&(*T)->lchild);//构造左子树
CreateBiTree(&(*T)->rchild);//构造右子树
}
return OK;
}二叉树遍历算法的应用——复制二叉树
如果是空树,递归结束;
否则,申请新结点空间,复制根结点
递归复制左子树
递归复制右子树
int Copy(BiTree T,BiTree &NewT)
{
if(T==NULL)
{
NewT=NULL;
return 0;
}
else
{
NewT=new BiTNode;
NewT->data=T->data;
Copy(T->lchild,NewT->lchild);
Copy(T->rchild,NewT->rchild);
}
}