今天,接着上一期的博文,继续推进!!
请看下面的的代码 :>
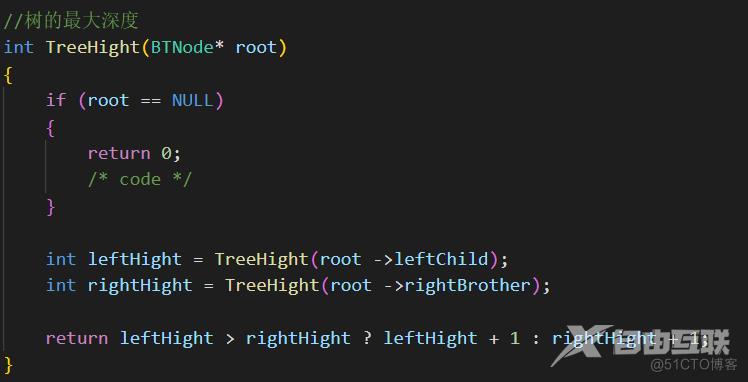
求一棵树的高度,为何需要存储起来呢?
解答这个问题之前,需要稍微改动一下,上述的代码!会发现上述代码有很大的好处!
//二叉树的高度
int TreeHight(BTNode* root)
{
if(root == NULL)
{
return 0;
}
return TreeHight(root ->leftChild) > TreeHight(root ->rightBrother)
? TreeHight(root ->leftChild) + 1
: TreeHight(root ->rihgtBrother) + 1;
}好了,各位好友!!再一次手搓了一遍求树的高度的代码!!
我们发现上述的改动很明显!!那就是我们删掉了保存值!!
那么这样会引发什么问题呢?
其实,还是直接先说答案好了。没有保存值的情况下,会造成递归遍历的次数成指数增长!!
举一个例子,请看下图 :>
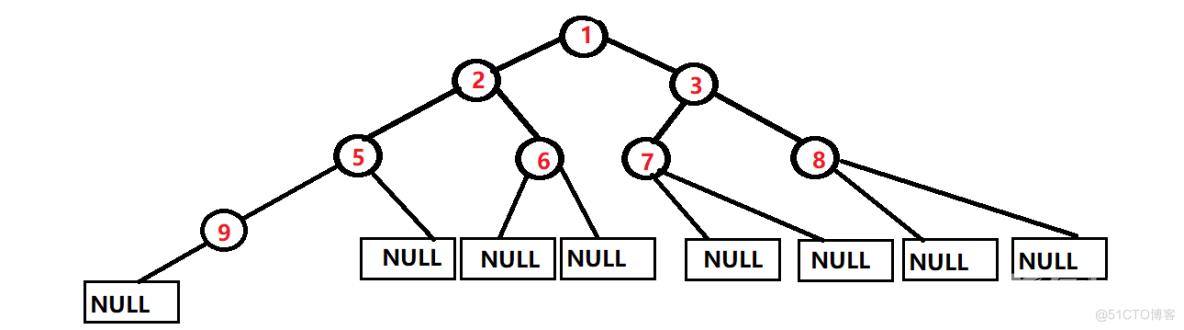
如果没有保存值的情况下,对于最底层的数字,被访问次数会大到超乎想象!!
假如,访问的是层级为10的话,那么它的次数是1024次
而当层级是20的时候,它的次数是100万!
而当层级为30的时候,被访问的次数将会达到10亿!!
是不是看着这些数字,特别敏感,其实这是一个等比数列 :> 2^n
上述的次数,是由递归展开图,总结出来的!!
显然,这样子,此种很挫的写法。时间复杂度就是 O(n^2)
其实,求 树的最大高度,对于底层的访问仅仅一次就可以了!此时,时间复杂度是O(n)
希望老友们,可以好好体会!!在这里,对递归的要求是蛮高的!!
另外,还要说明一下, 代码中 有一个 “+ 1”是怎么回事!!
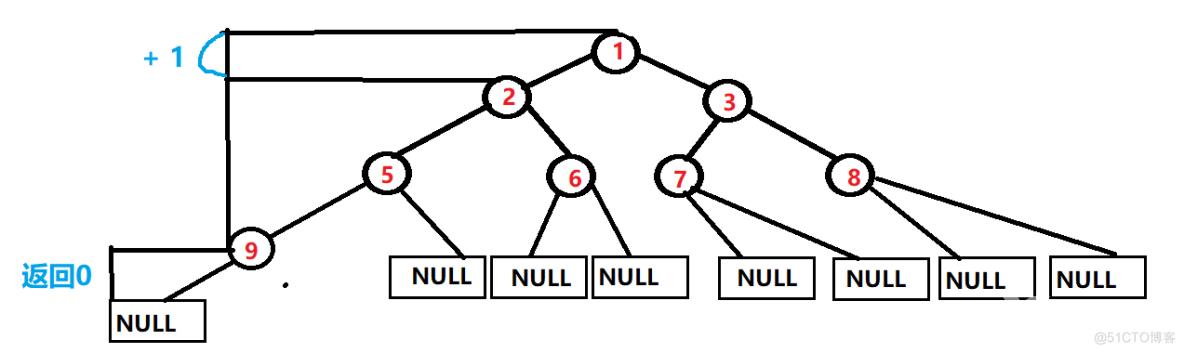
-----> 当递归完成左子树或者右子树的时候,此时的高度是 从子树到叶子结点的距离,而一开始的子树到根的距离还有一个单位的长度!!
下面,开始另一段代码 :>
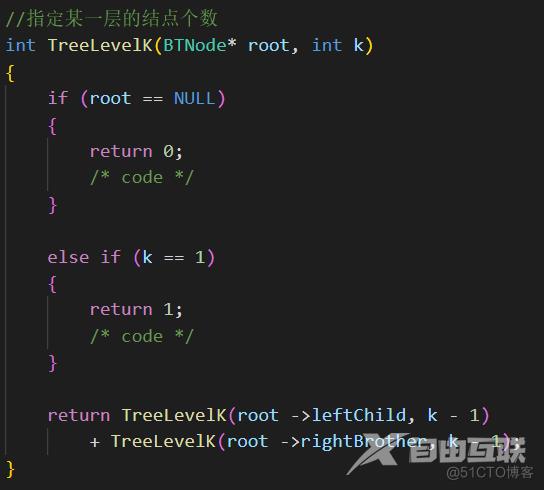
另外,还遗漏了一个小细节,这里的 K 的取值范围,是需要断言一下的!
------> 断言 K 的范围 “assert(K > 0);”
其实这段代码,比刚才的求树的高度难度有所提升,理解上更进了一步!!
那么,该如何解读才可以呢!在这里,涉及到相对距离,什么意思呢?
请看下列图示 :>
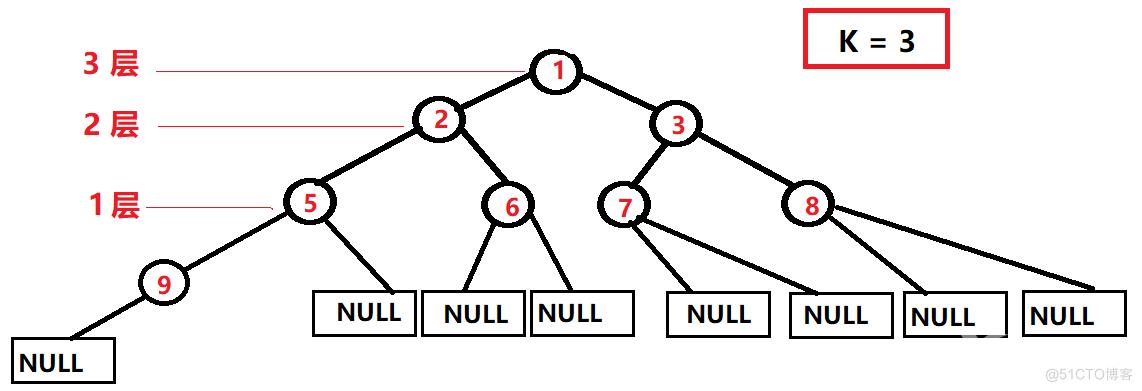
上述二叉树层为四层数,而现在求的是第三层的结点个数!相对位置怎么样呢?---> K == 3
那么从根结点开始相对于第三层就是距离3个单位
对于第二层而言,便是距离为2个单位
则第三层,距离就是1个单位了
为了方便理解,递归过程的展开图是要画出来的!请看下面图示 :>
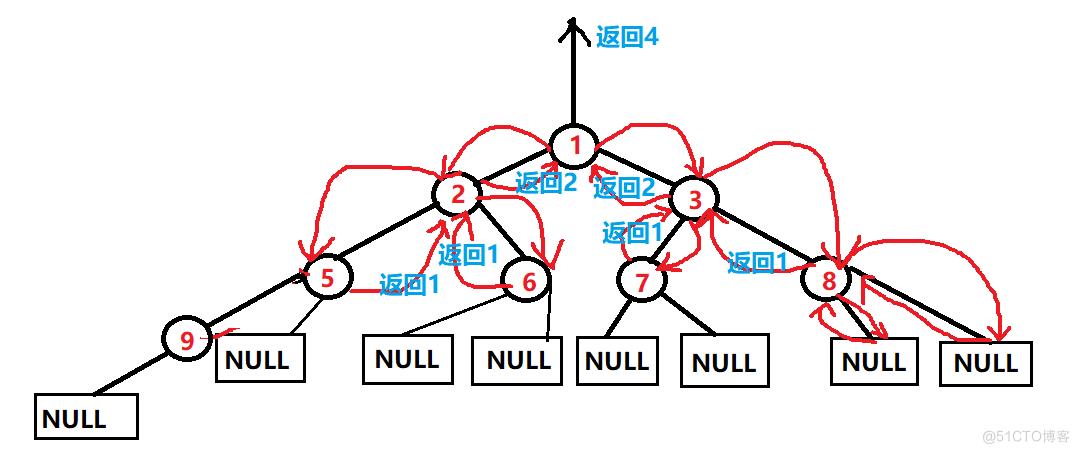
在这里并没有什么所谓 0层!0层没有任何意义!!
这个时候再看一下代码,是不是理解就容易多了!!其实核心思想:相对位置的理解
注意,空子树的时候就返回 0 就可以了;那么 K == 4 层级的时候,显然是返回 1 个结点,毕竟 结点 5 的右子树是空树嘛!
至此,上一期学到的内容,重要的难点和一些细节,就已经讲解完成了!!各位老友,有没有真正 Get 到
