递归定义
若一个对象部分地包含它自己,或用它自己给自己定义,则称这个对象是递归的;若一个过程直接地或间接地调用自己,则称这个过程是递归的过程。递归就是定义体中再次出现被定义项本身。
被定义项在定义体中再次出现时,要满足两个要求:更小的尺度,最小尺度上要有明确定义。
例如:递归求n的阶乘
具有递归特性的数据结构:二叉树、广义表
以下三种请况常常用到递归方法:
①递归定义的数学函数
②具有递归特性的数据结构
③可递归求解的问题
递归问题——用分治法求解
分治法:对于一个较为复杂的问题,能够分解成几个相对简单的且解法相同或类似的子问题来求解
必备的三个条件
1.能将一个问题转变成一个新问题,而新问题与原问题的解法相同或类同,不同的仅是处理的对象,且这些处理对象是变化有规律的
2.可以通过上述转化而使问题简化
3.必须有一个明确的递归出口,或称递归的边界
分治法求解递归问题算法的一般形式:
void p(参数)
{
if(递归结束条件)
可直接求解步骤;-----基本项
else
p(较小的参数);-----归纳项
}函数调用过程
调用前,系统完成:
(1)将实参,返回地址等传递给被调用函数
(2)为被调用函数的局部变量分配存储区
(3)将控制转移到被调用函数的入口
调用后,系统完成:
(1)保存被调用函数的计算结果
(2)释放被调用函数的数据区
(3)依照被调用函数保存的返回地址将控制转移到调用函数
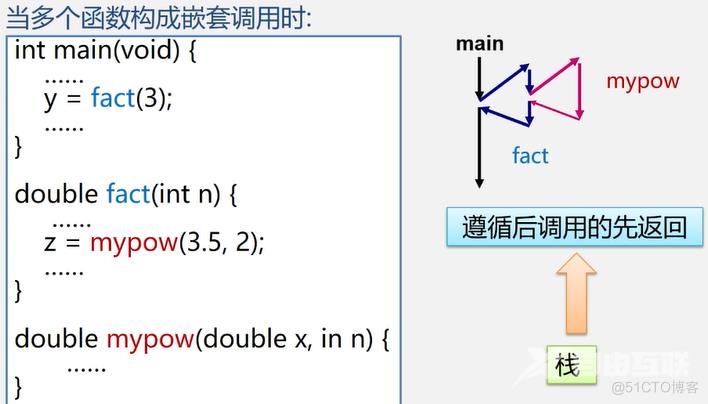

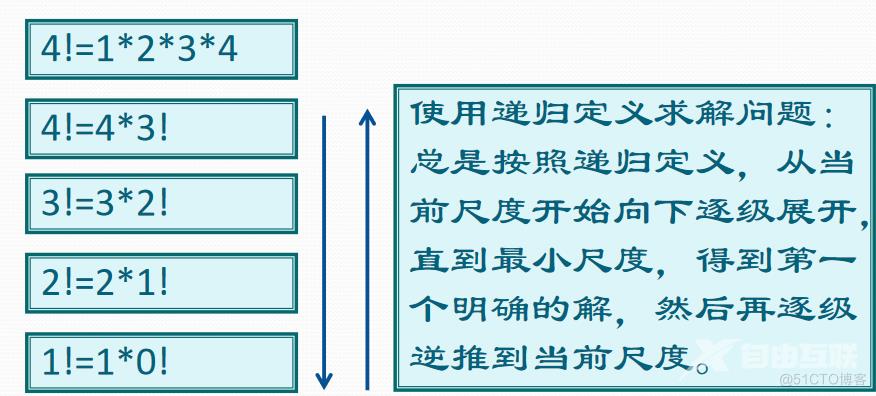
递归函数调用的实现
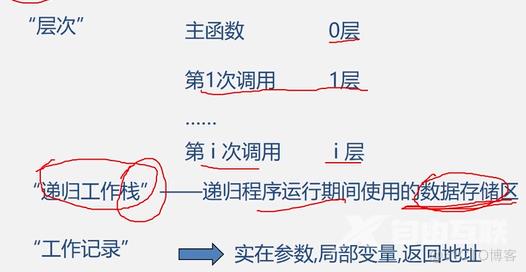
递归的优缺点
优点:结构清晰,程序易读
缺点:每次调用要生成工作记录,保存状态信息,入栈;返回时要出栈,恢复状态信息。时间开销大。
递归→非递归的方法
方法1:尾递归、单向递归→循环结构
方法2:自用栈模拟系统的运行时栈

单项递归→循环结构

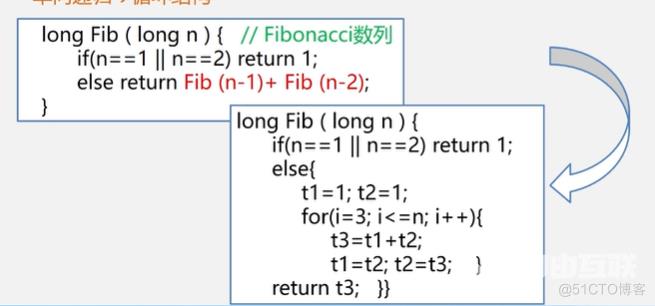
借助栈改写递归的方法(了解)


n阶汉诺塔问题
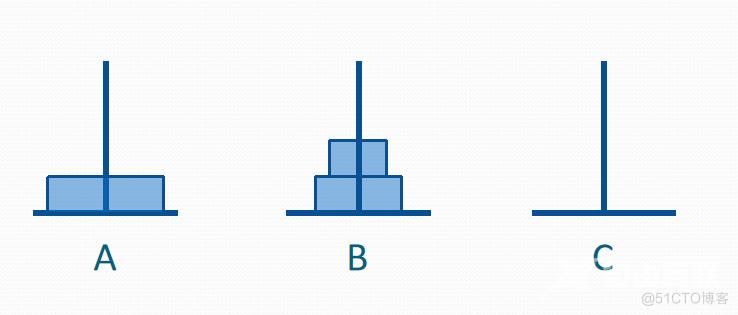
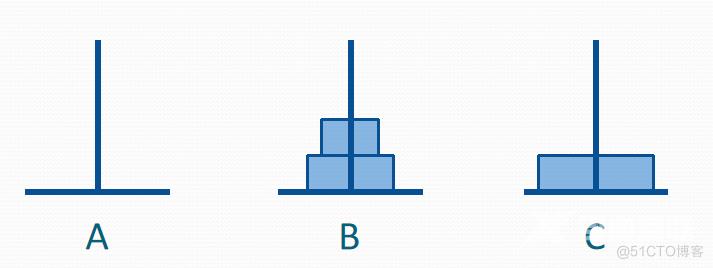
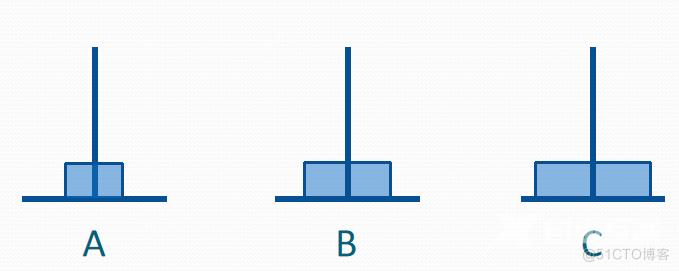
假设有3个分别命名为A、B和C的塔座,在塔座A上插有n个直径大小各不相同、依小到大 编号为l,2,…,n的圆盘,现要求将A上的n个圆盘移至C上并仍按同样顺序叠排,圆盘移动时必须遵循下列规则:
(1)每次只能移动一个圆盘;
(2)圆盘可以移至A、B和C中的任一塔座上;
(3)任何时刻都不能将一个较大的圆盘压在较小圆盘之上。
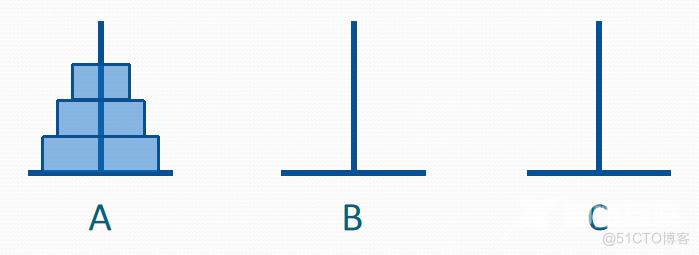
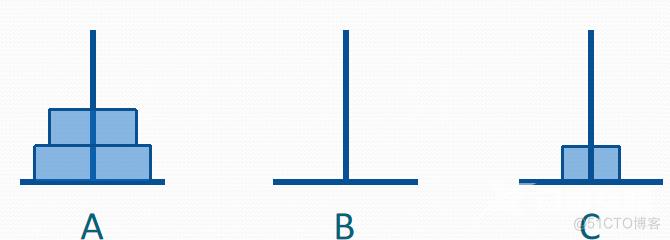
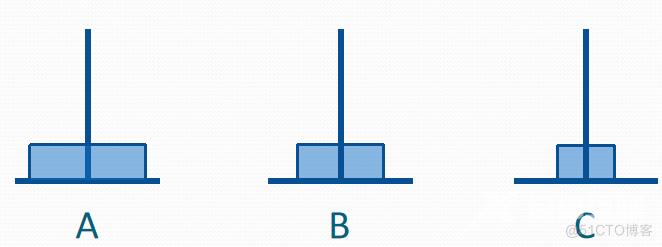
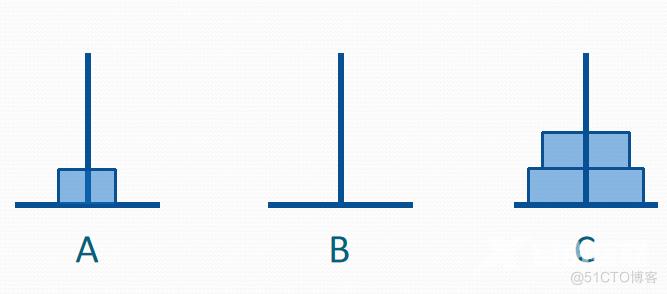
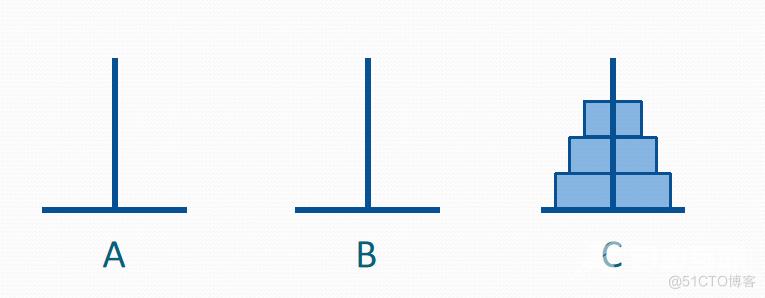
n阶汉诺塔问题的解决方案:
将1~n号从A经B移至C
若n=1,则直接将A移到C
否则:
1.将1~n-1号从A经C移到B
2.将n号从A移到C
3.将1~n-1号从B经过A移到C
3阶汉诺塔问题
将1~3号从A经过B移到C
1.将1~2号从A经C移到B
1.将1~1号从A经B移到C A→C
2.将2号从A移到B A→B
3.将1~1号从C经A移到B C→B
2.将3号从A移到C A→C
3.将1~2号从B经过A移到C
1.将1~1号从B经C移到A B→A
2.将2号从B移到C B→C
3.将1~1号从A经B移到C A→C
重要练习——5阶汉诺塔
将1~5号从A经B移到C
1.将1~4号从A经C移到B
1.1将1~3号从A经B移到C
1.1.1将1~2号从A经C移到B
1.1.1.1将1~1号从A经B移到C A→C
1.1.1.2将2号从A移到B A→B
1.1.1.3将1~1号从C经A移到B C→B
1.1.2将2号从A移到C A→C
1.1.3将1~2号从B经A移到C
1.1.3.1将1~1号从B经C移到A B→C
1.1.3.2将2号从B移到A B→A
1.1.3.3将1~1号从A经B移到C A→C
1.2将4号从A移到B A→B
1.3将1~3号从C经过A移到B
1.3.1 将1~2号从C经B移到A
1.3.1.1将1~1号从C经A移到B C→B
1.3.1.2将2号从C移到A C→A
1.3.1.3 将1~1号从B经C移到A B→A
1.3.2将3号从C移到B C→B
1.3.3 将1~2号从A经C移到B
1.3.3.1将1~1号从A经B移到C A→C
1.3.3.2 将2号从A移到B A→B
1.3.3.3 将1~1从C经A移到B C→B
2.将5号从A移到C A→C
3.将1~4号从B经过A移到C
3.1 将1~3号从B经C移到A
3.1.1将1~2号从B经A移到C
3.1.1.1 将1~1号从B经C移到A B→A
3.1.1.2 将2号从B移到C B→C
3.1.1.3 将1~1号从A经B移到C A→C
3.1.2 将3号从B移到A B→A
3.1.3 将1~2号从C经B移到A
3.1.3.1 将1~1号从C经A移到B C →B
3.1.3.2 将2号从C移到A C→A
3.1.3.3 将1~1号从B经C移到A B→A
3.2 将4号从B移到C B→C
3.3 将1~3号从A经B移到C
3.3.1 将1~2号从A经C移到B
3.3.1.1将1~1号从A经B移到C A→C
3.3.1.2 将2号从A移到B A→B
3.3.1.3 将1~1号从C经A移到B C→B
3.3.2 将3号从A移到C A→C
3.3.3 将1~2号从B经A移到C
3.3.3.1 将1~1号从B经C移到A B→A
3.3.3.2 将2号从B移到C B→C
3.3.3.3 将1~1号从A经B移到C A→C
代码实现
#include<stdio.h>
int c=0;
void move(char x,int n,char z)
{
printf("%d.move disk%d from %c to %c\n",++c,n,x,z);
}
void hanoi(int n,char x,char y,char z)
{
if(n==1)
move(x,1,z);
else
{
hanoi(n-1,x,z,y);
move(x,n,z);
hanoi(n-1,y,x,z);
}
}
int main()
{
hanoi(5,'A','B','C');
return 0;
}