布隆过滤器
用一句话来说,布隆过滤器是为了解决查询一个元素是否存在于某个集合之中。
例如:50亿个用户ID,查询某ID是否在这50亿集合之中。
50亿*8字节大约为50GB,内存占用极大。
所以一般采用 位数组,以及位数组的延伸设计:布隆过滤器。
在学习布隆过滤器之前,我们需要有些基础性概念:
哈希函数
哈希函数,即散列函数。它可以任意长度的输入通过算法转换成一个定长的输出,这个输出就是散列值,或者叫哈希值。
因为是无穷对应有限,则必有多个输入对应相同的输出,即散列冲突,或叫哈希冲突。
哈希算法有以下特点:
- 从输出无法推导出输入。
- 散列冲突的概率要尽可能小。
- 数据敏感,对输入的简单修改会导致输出的巨大差异。
位数组
位数组本质上是一个超长的bit数组,数组元素只能为0或1。
根据上文,如果50亿个用户ID是有序的,使用bit数组实际上很好判断。
将每个ID映射到数组下标之中,用1代表存在,0代表不存在,如果有一段数学意义上连续的ID,还可以用一位数组下标映射一段ID,内存占用将更小。
但如果用户ID不是自增的,如果50亿用户ID,按照ID为10位来计算,将有超过90亿种可能排列,使用位数组要占用超过100GB内存。
这几乎是无法接受的。
布隆过滤器
布隆过滤器(Bloom Filter)的核心组件是一个超长的位数组和若干个哈希函数 。
布隆过滤器的查询复杂度为O(k),k为哈希函数的个数,并且支持并发修改或查询。
设数组长度为m,哈希函数个数为k。
在初始状态下,数组每个元素都被设置为0。
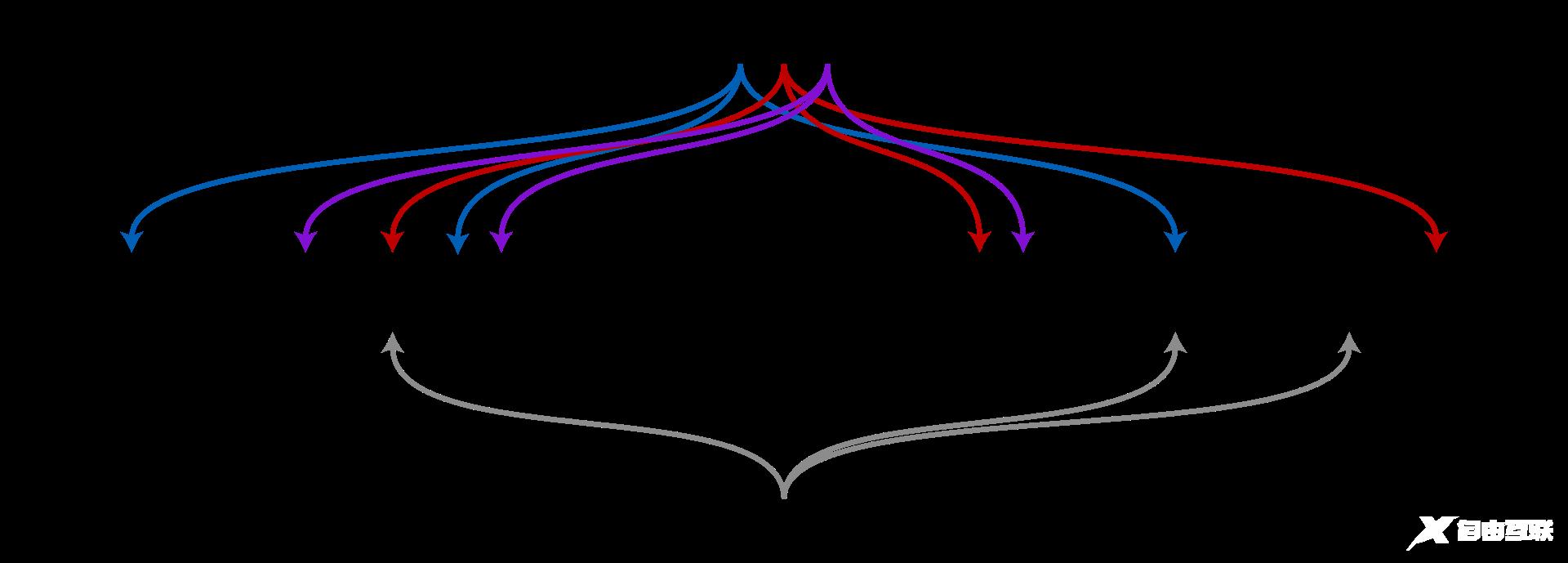
当有元素加入过滤器时,通过k个哈希函数,计算k个数组下标,并将数组下标所在元素置为1。
当查询时,再次通过k个哈希函数,计算得k个数组下标,并检查数组下标是否全部为1。若是,则该元素存在于集合中,反之则不存在于集合中。
误判问题
通过上述插入与查询逻辑可以推导得:
布隆过滤器不会将集合里的元素误判为不在集合之中。
用具象的话来理解就是:宁可放过,绝不误伤。
这很好理解,如果在集合内的元素,哈希计算后的下标所对应的元素都为1,不会出现误伤现象。
而如果反过来想想,如果这个元素不在集合之中,由于哈希冲突,在极端情况下,该元素所有哈希计算后的下标对应元素都为1,那么可能会造成不在集合之中的元素放行。
所以造成了布隆过滤器的误判问题。
误判率计算
设数组长度为m,哈希函数个数为k,数组内已添加n个元素。
则可以推导:
-
数组中某一特定的位在进行元素插入时的 Hash 操作中没有被置1的概率是:
$$ 1-\frac{1}{m} $$
-
在所有 k 次 Hash 操作后该位都没有被置 1 的概率是: $$ (1-\frac{1}{m})^{k} $$
-
如果我们插入了 n 个元素,那么某一位仍然为 0 的概率是: $$ (1-\frac{1}{m})^{kn} ≈ e ^ \frac{-kn}{m} $$
-
该位为 1 的概率是: $$ 1 - (1-\frac{1}{m})^{kn} ≈ 1 - e ^ \frac{-kn}{m} $$
-
则经过 k 个哈希函数后仍然错误的概率为: $$ (1 - e ^ \frac{-kn}{m}) ^ {k} $$
求最优参数
根据布隆过滤器性质可知,k 必须为整数。
在一般情况下,m 与 n 不在开发者能调控的范围之内。
所以一般最优参数都指的是求 k 的最优参数,即:在 k 为何值时,过滤器的误判率最小。
根据数学性质,对于给定的 m 和 n,最小化误报概率的 k 值为: $$ k = \frac{m}{n}ln2\quad(ln2≈0.693) $$
布隆过滤器的删除问题
在布隆过滤器中,一般情况下是无法删除元素的,因为存在哈希冲突,所以可能会把其他元素对应的下标置为0,导致未被删除的元素被误认为不存在集合之中。
为了解决这个问题,可以采用 计数删除 方案。
简单来说,为每个下标计数,如果下标被置为 1 则为计数器 +1,反之则减1。
这样会保留下来其他元素的映射信息。
计数回绕
同时,这种方法会存在计数回绕问题。
计数器类型为了节省内存,一般用unsigned修饰,它只能表示非负整数,因此其取值范围是从0到最大值。例如,如果使用8位无符号整数,其取值范围是0到255。
当计数器的值达到最大值时,再进行+1操作会导致计数器值溢出,即超出了它能表示的最大值,导致计数器的值变为0。这个过程就是计数回绕,这导致当哈希冲突次数过多,超过计数器类型能表示的范围时,计数器反而会变成0,影响布隆过滤器的判断。
同理,当计数器为0且 -1 时,也会导致计数器值溢出。
