Computational physics 计算物理 exact diagonalization 精确对角化1

背景介绍

在量子力学中，量子态所处的空间被称为希尔伯特空间，希尔伯特空间在数学上的定义就是无限维矢量空间。

在希尔伯特空间中，存在着许多组基矢量，只要这些基矢量两两互不平行即可（这些基矢量无需是正交的）。

\(a|\psi\rangle\) 可以看作与 \(|\psi\rangle\) 是相同的。

因为我们事先难以知道一些不常规的哈密顿算符的本征态波函数的形式，所以在数值求解中，我们会事先选择我们熟知的基矢量，并用这些基矢量的线性组合来表示出哈密顿量的本征态矢量。
这些我们熟悉的基矢量可以是 \(\delta(x-x')\)，谐振子基矢量，一维无限深方势阱的基函数。

为了方便讨论，认为这些基矢量是两两正交的：

\[\langle\psi_i|\psi_j\rangle=\delta_{ij} \]

系统的本征态矢量可以由基矢量的线性组合表示出来（注意，因为我们要求的是一个体系的本征态与其对应的能量本征值，因此这个态矢量\(|\Psi\rangle\)就是哈密顿算符的本征态矢量）：

\[|\Psi \rangle =\sum_i{a_i|\psi _i\rangle} \]

\[\hat{H}|\Psi \rangle =E|\Psi \rangle \]

将基矢量的线性组合表示带入薛定谔方程，得到：

\[\sum_i{a_i\langle \psi _j|\hat{H}|\psi _i\rangle}=E\sum_i{a_i\langle \psi _j|\psi _i\rangle} \]

写作：

\[\sum_i{a_iH_{ji}}=Ea_j \]

其中，\(H_{ji}=\langle \psi _j|\hat{H}|\psi _i\rangle=\int_{-\infty}^{\infty}{\mathrm{d}x\cdot \psi _{j}^{*}\left( x \right) H\psi _i\left( x \right)}\)
写作矩阵就是这样的形式：

\[\left[ \begin{matrix} H_{11}& H_{12}& \cdots& \cdots\\ H_{21}& H_{22}& \cdots& \cdots\\ \vdots& & & \\ \vdots& & & \\ \end{matrix} \right] \left[ \begin{array}{c} c_1\\ c_2\\ \vdots\\ \vdots\\ \end{array} \right] =E\left[ \begin{array}{c} c_1\\ c_2\\ \vdots\\ \vdots\\ \end{array} \right] \]

我们接下来所要做的就是构造出这个哈密顿量的矩阵，然后求解特征值与特征向量。
特征值中最小的值就是系统基态能量值。

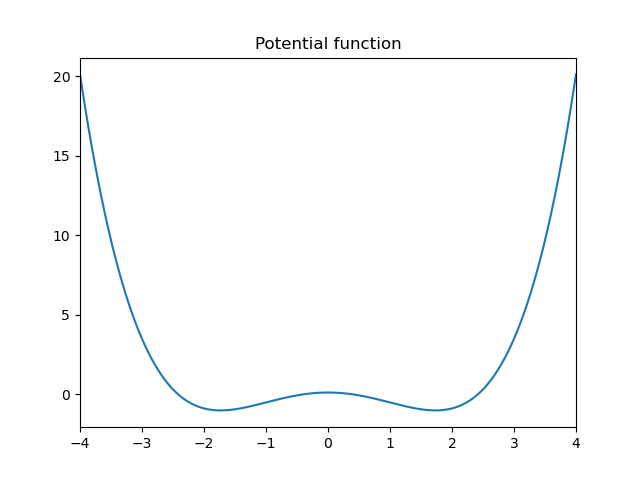
接下来，我将介绍两个例子，所用的势函数为 \(V\left( x \right) =\frac{m\omega _{0}^{2}}{2}\left[ \frac{\left( x^2-x_{0}^{2} \right)}{4x_{0}^{2}}-x^2 \right]\) .

自然差分基底法

所谓自然差分基底，就是把 \([0,L]\)，差分为 \(n-1\) 个等长度区间，于是就有 \(n\) 个节点。
区间长度是：\(\Delta x=\frac{L}{n-1}\)，每一个节点的坐标可以表示为：\(x_i=i\Delta x\)，其中 \(i=0,\cdots ,n-1\)

写出哈密顿量在坐标表象下的形式：

\[-\frac{\hbar ^2}{2m}\frac{\partial ^2\Psi \left( x \right)}{\partial x^2}+V\left( x \right) \Psi \left( x \right) =E\Psi \left( x \right) \]

按照经典的差分方法可以写作：

\[-\frac{\hbar ^2}{2m}\frac{\Psi \left( x_{n+1} \right) -2\Psi \left( x_n \right) +\Psi \left( x_{n-1} \right)}{\Delta x^2}+V\left( x_n \right) \Psi \left( x_n \right) =E\Psi \left( x_n \right) \]

于是，哈密顿量的矩阵表示就是：

\[\left[ \begin{matrix}{} \frac{\hbar ^2}{m\left( \Delta x \right) ^2}+V\left( x_1 \right)& -\frac{\hbar ^2}{2m\left( \Delta x \right) ^2}& \cdots& \cdots& \cdots\\ -\frac{\hbar ^2}{2m\left( \Delta x \right) ^2}& \frac{\hbar ^2}{m\left( \Delta x \right) ^2}+V\left( x_2 \right)& -\frac{\hbar ^2}{2m\left( \Delta x \right) ^2}& \cdots& \cdots\\ \vdots& -\frac{\hbar ^2}{2m\left( \Delta x \right) ^2}& \frac{\hbar ^2}{m\left( \Delta x \right) ^2}+V\left( x_3 \right)& -\frac{\hbar ^2}{2m\left( \Delta x \right) ^2}& \cdots\\ \vdots& \cdots& \cdots& \cdots& \cdots\\ \vdots& \cdots& \cdots& \cdots& \cdots\\ \end{matrix} \right] \]

代码可见知乎用户hahakitty的文章：
https://zhuanlan.zhihu.com/p/264940250

谐振子基底法

谐振子基底，是势函数为谐振子势的哈密顿量的本征态基矢量。
详情可见Cohen-Tannoudji的量子力学第一卷第五章。

由于量子力学中，已经用了简单的方法，将坐标表象下繁琐的求解过程，转换到了谐振子基函数的表象，定义了创生算符与湮灭算符，可以用这两个算符去表示出其他的物理量。
写出 \(a\) 与 \(a^{\dagger}\) 的矩阵表示（Page504）：

\[a=\left[ \begin{matrix} 0& \sqrt{1}& \cdots& \cdots\\ \vdots& 0& \sqrt{2}& \cdots\\ \vdots& \vdots& 0& \cdots\\ \vdots& \vdots& \vdots& \ddots\\ \end{matrix} \right] , a^{\dagger}=\left[ \begin{matrix} 0& \cdots& \cdots& \cdots\\ \sqrt{1}& 0& \cdots& \cdots\\ \vdots& \sqrt{2}& 0& \cdots\\ \vdots& \vdots& \vdots& \ddots\\ \end{matrix} \right] \]

\[x=\sqrt{\frac{m\omega}{2\hbar}}\left( a^{\dagger}+a \right) \]

\[p=i\sqrt{\frac{1}{2m\hbar \omega}}\left( a^{\dagger}-a \right) \]

\[p^2=-\frac{1}{2m\hbar \omega}\left( {a^{\dagger}}^2-a^{\dagger}a-aa^{\dagger}+a^2 \right) \]

哈密顿量为：

\[H=\frac{p^2}{2m}+\frac{m\omega _{0}^{2}}{2}\left[ \frac{\left( x^2-x_{0}^{2} \right)}{4x_{0}^{2}}-x^2 \right] \]

将以上矩阵代入哈密顿量算符，注意，与 \(x\) 相加的 \(x_0\) 要写作单位矩阵的形式，而不是直接在每个 \(x\) 的矩阵元上减去一个常数，另外所有的乘法都是矩阵乘法。

构造出哈密顿量的矩阵之后，直接用：

点击查看代码

numpy.linalg.eig()

求出特征值与特征向量。

那么如何用特征向量求得坐标表象下波函数的图像呢，需要应用：

点击查看代码

np.polynomial.hermite.Hermite()

具体用法见https://www.osgeo.cn/numpy/reference/routines.polynomials.hermite.html 注意，要用的是物理学家用的厄米特多项式序列。

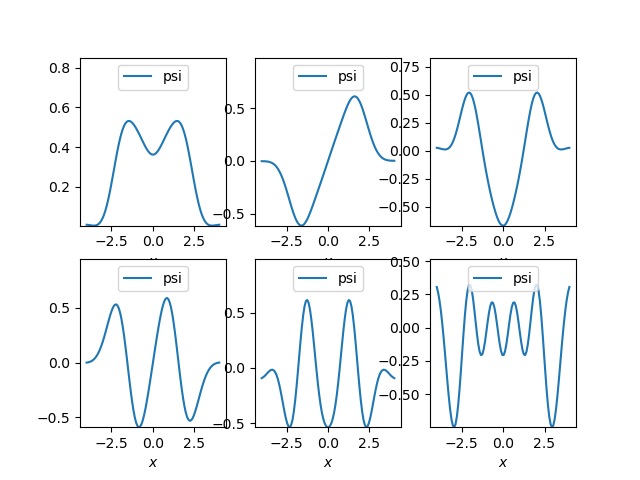
列出求解代码与图片：

点击查看代码

import numpy as np
import matplotlib.pyplot as plt
import math

class harmonic_osci:
    def __init__(self,Hamiltonian,
                xmin=-4,xmax=4,ninterval=100,ndim=10):
        self.nint=ninterval
        self.x = np.linspace(xmin, xmax, ninterval)
        self.a=self.annilation(ndim)
        self.a_d=self.creation(ndim)
        self.X=(1/np.sqrt(2))*(self.a_d+self.a)
        self.P_square=(-1/2)*(np.dot(self.a_d,self.a_d)-np.dot(self.a_d,self.a)
                             -np.dot(self.a,self.a_d)+np.dot(self.a,self.a))
        self.H=Hamiltonian(self.X,self.P_square,np.eye(ndim+1))
        self.eigE, self.eigV = self.eig_solve()

    def annilation(self, N):
        a=np.sqrt(np.linspace(1,N,N))
        return np.zeros((N+1,N+1))+np.diag(a,1)

    def creation(self,N):
        a=np.sqrt(np.linspace(1,N,N))
        return np.zeros((N+1,N+1))+np.diag(a,-1)

    def eig_solve(self):
        '''解哈密顿矩阵的本征值,本征向量,并对本征向量排序'''
        w, v = np.linalg.eig(self.H)
        idx_sorted = np.argsort(w)
        return w[idx_sorted], v[:, idx_sorted]

    def wave_func(self, n=0):
        return self.eigV[:, n]

    def eigen_value(self, n=0):
        return self.eigE[n]
    
    def check_eigen(self, n=0):
        coef1=np.zeros_like(self.eigV[:,n])
        for i in range(len(self.eigV[:,n])):
            coef1[i]=(1/np.pi**(1/4))*(1/np.sqrt(2**i*math.factorial(i)))*self.eigV[:,n][i]
        #Hermite Polynomials
        Psi=np.polynomial.hermite.Hermite(coef1)(self.x)*np.exp(-self.x**2/2)
        
        plt.plot(self.x, Psi,label='$\psi$')
        plt.legend(loc='upper center')
        plt.xlabel(r'$x$')
        plt.ylim(Psi.min(), Psi.max() * 1.6)
    
def Q4(x,p_square,x0,m=1,omega_0=1):
    return p_square/(2*m)+(m*omega_0**2)/2*((np.dot((np.dot(x,x)-np.dot(x0,x0)),np.dot(x,x)-np.dot(x0,x0)))/4-np.dot(x,x))

Qu4=harmonic_osci(Q4)

for i in range(6):
    print(Qu4.eigen_value(n=i))
    plt.subplot(2,3,i+1)
    Qu4.check_eigen(n=i)
plt.show()

【本文由：湖北阿里云代理 http://www.558idc.com/aliyun.html 复制请保留原URL】