leetcode 542. 01 Matrix 01 矩阵(中等)

判断使用动态规划思路解决问题，先定义一个数组dp[][]来，找到状态转移方程式。本题需要从左上开始搜索一次，右下开始搜索一次。 一、题目大意

标签: 动态规划

https://leetcode.cn/problems/01-matrix

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。
示例 1：

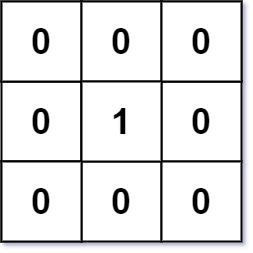
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

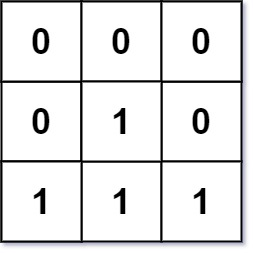
输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• mat 中至少有一个 0

二、解题思路

判断使用动态规划思路解决问题，先定义一个数组dp[][]来，找到状态转移方程式。本题需要从左上开始搜索一次，右下开始搜索一次。

三、解题方法 3.1 Java实现

public class Solution {
    public int[][] updateMatrix(int[][] mat) {
        int n = mat.length;
        int m = mat[0].length;
        int[][] dp = new int[n][m];
        // mat[i][j] == 1, dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i+1][j], dp[i][j+1])
        // mat[i][j] == 0, dp[i][j] = 0
        // 将dp中的值置为最大
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                dp[i][j] = Integer.MAX_VALUE - 1;
            }
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (mat[i][j] == 0) {
                    dp[i][j] = 0;
                } else {
                    if (j > 0) {
                        dp[i][j] = Math.min(dp[i][j], dp[i][j - 1] + 1);
                    }
                    if (i > 0) {
                        dp[i][j] = Math.min(dp[i][j], dp[i - 1][j] + 1);
                    }
                }
            }
        }
        for (int i = n - 1; i >= 0; i--) {
            for (int j = m - 1; j >= 0; j--) {
                if (mat[i][j] != 0) {
                    if (j < m - 1) {
                        dp[i][j] = Math.min(dp[i][j], dp[i][j + 1] + 1);
                    }
                    if (i < n - 1) {
                        dp[i][j] = Math.min(dp[i][j], dp[i + 1][j] + 1);
                    }
                }
            }
        }

        return dp;
    }
}

四、总结小记

• 2022/6/19 夏至未到，温度已经到了；涉及到数组问题行列老是搞混