极坐标系在数据可视化中的巧妙运用

常规的柱状图，散点图等展示形式，都是在笛卡尔坐标系中进行展示，是使用最为广泛的图表。这些图表在展示信息方面具有扎实的基础，但是却缺乏了一丝创意。

通过极坐标转换，可以将普通的图表变的更加的具有创意，比如以下图表，展示了各个国家的制造指数

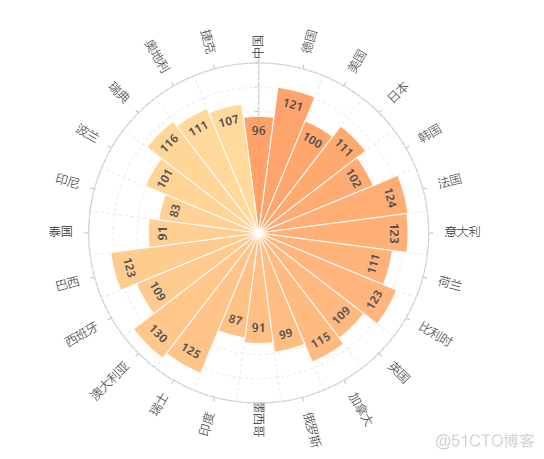
这样的图表形式有一个好听的名字，叫做南丁格尔玫瑰图，其本质就是极坐标系中的柱状图。

在matplotlib中，可以轻松的使用极坐标绘图，基本用法如下

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> r = np.arange(0, 2, 0.01)
>>> theta = 2 * np.pi * r
>>> ax = plt.subplot(111, projection='polar')
>>> ax.plot(theta, r)
>>> ax.set_rticks([0.5, 1, 1.5, 2])
>>> plt.show()

将projection参数的值设置为polar,表示该axes将采用极坐标系，接下来只需要指定极坐标系中的点的坐标即可，输出结果如下

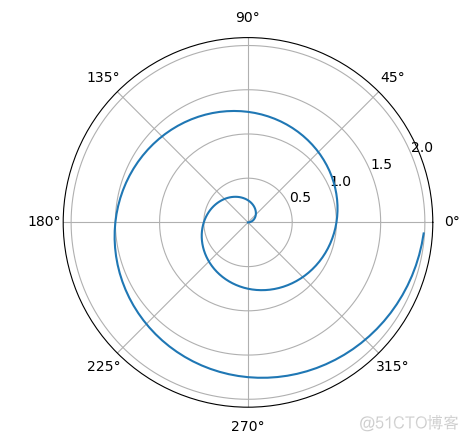
在matplotlib的极坐标系中，确定点的坐标需要两个值，第一个值是点的弧度值，第二个是半径，简单理解，弧度看做是笛卡尔坐标系中的x轴坐标，半径看做是笛卡尔坐标系中的y轴坐标。

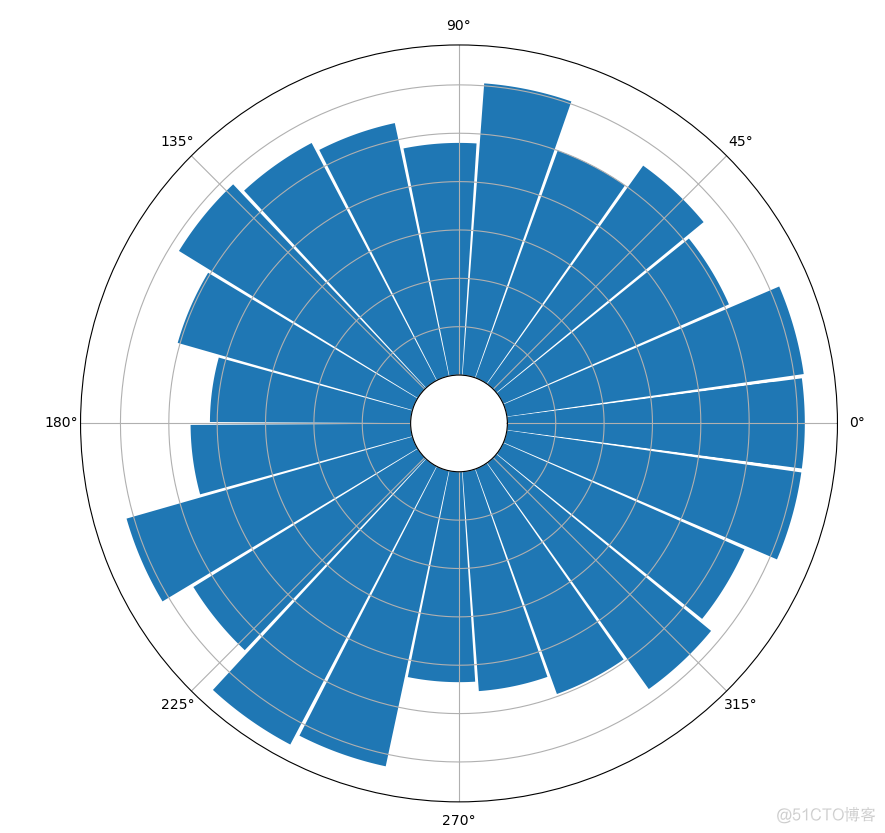
理解了极坐标中的点的位置，就可以轻松绘制柱状图了，代码如下

>>> vals = [123, 124, 102, 111, 100, 121, 96, 107, 111, 116, 101, 83, 91, 123, 109, 130, 125, 87, 91, 99, 115, 109, 123, 111]
>>> theta = np.linspace(0, 2 * np.pi, len(vals))
>>> ax = plt.subplot(111, projection='polar')
>>> ax.bar(theta, vals, width = 2 * np.pi / len(vals))
>>> ax.tick_params(labelleft=False)
>>> plt.show()

输出结果如下

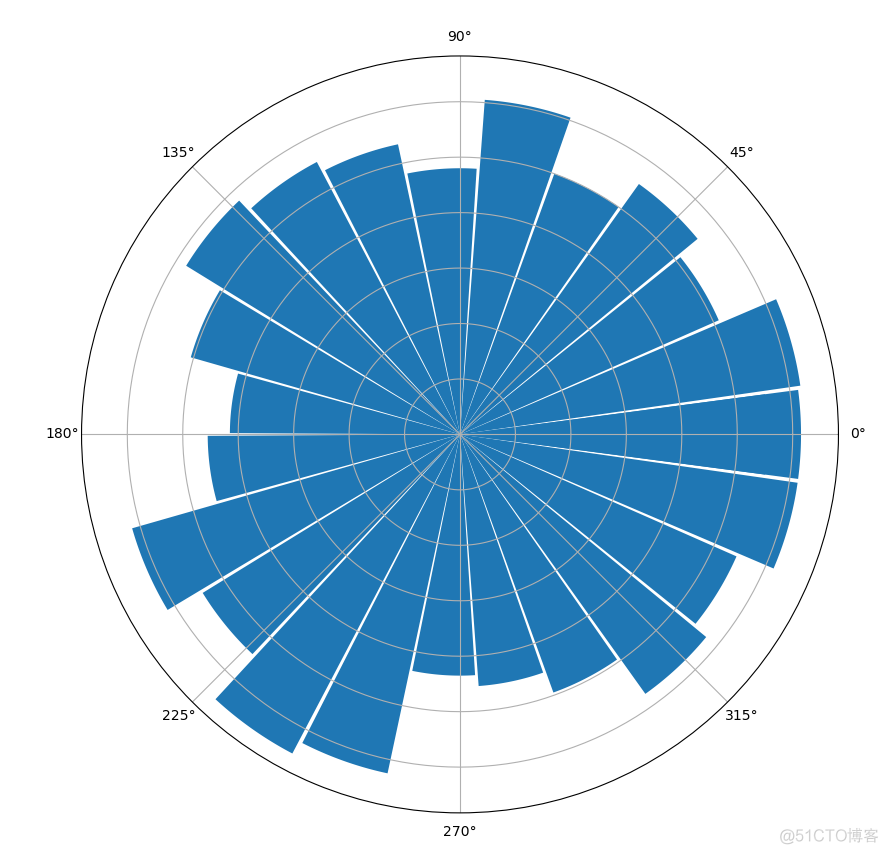
搞清楚极坐标系中的点的坐标，就可以快速的创建南丁格尔玫瑰图。在matplotlib中，还可以对极坐标系的范围进行设置，只选择其中部分区域来画。

第一个例子，选择弧度，代码如下

>>> vals = [123, 124, 102, 111, 100, 121, 96, 107, 111, 116, 101, 83, 91, 123, 109, 130, 125, 87, 91, 99, 115, 109, 123, 111]
>>> theta = np.linspace(0, 2 * np.pi, len(vals))
>>> ax = plt.subplot(111, projection='polar')
>>> ax.bar(theta, vals, width = 2 * np.pi / len(vals))
>>> ax.tick_params(labelleft=False)
>>> ax.set_thetamin(45)
>>> ax.set_thetamax(135)
>>> plt.show()

输出结果如下

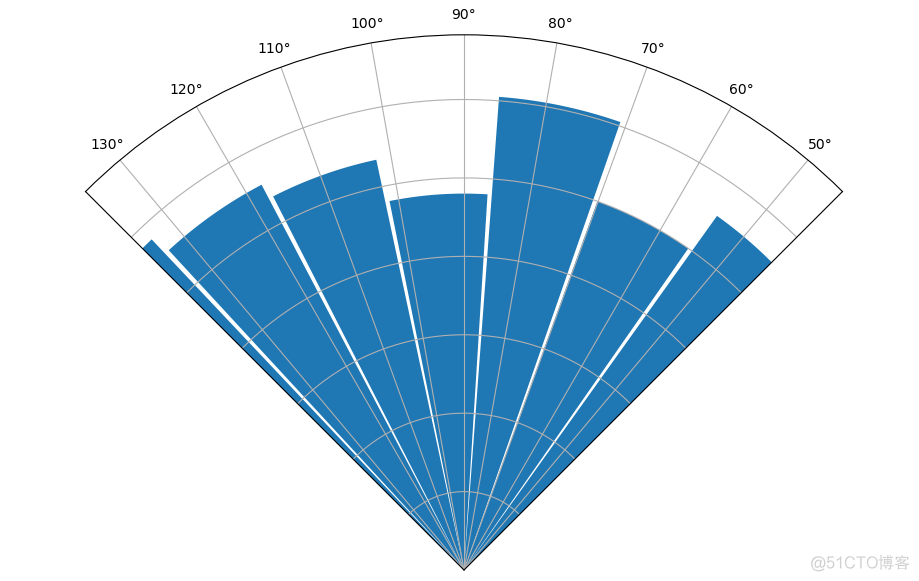
第二个例子，设置半径的范围，代码如下

>>> vals = [123, 124, 102, 111, 100, 121, 96, 107, 111, 116, 101, 83, 91, 123, 109, 130, 125, 87, 91, 99, 115, 109, 123, 111]
>>> theta = np.linspace(0, 2 * np.pi, len(vals))
>>> ax = plt.subplot(111, projection='polar')
>>> ax.bar(theta, vals, width = 2 * np.pi / len(vals))
>>> ax.tick_params(labelleft=False)
ax.set_rorigin(-20)
>>> plt.show()

输出结果如下

通过灵活的运用极坐标系，可以极大的丰富我们的图表展现形式，创建更具感染力的图表。

·end·

一个只分享干货的

生信公众号