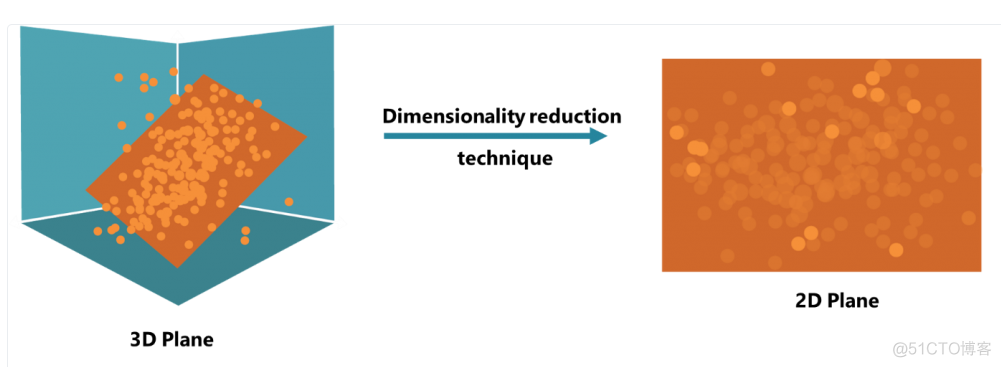
PCA是Principal components analysis的简称,叫做主成分分析,是使用最广泛的降维算法之一。所谓降维,就是降低特征的维度,最直观的变化就是特征的个数变少了。当然,不同于特征筛选,这里的降维主要是通过高维空间向低维空间投影来实现的,图示如下
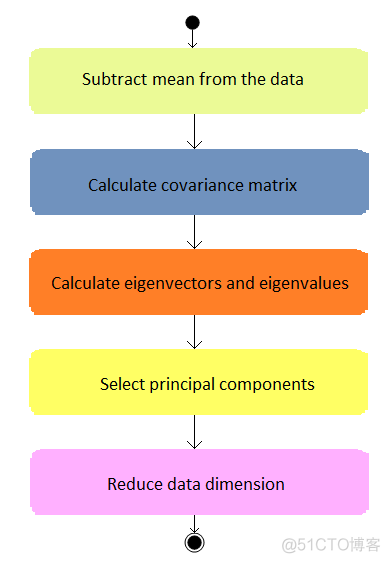
PCA算法的计算步骤分为以下5步
#### 1. 原始特征值的标准化
PCA中所用的标准化方式为零均值标准化,公式如下
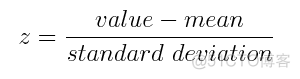
对于每一个特征,在原始值的基础上减去平均值,然后除以标准差,通过这一操作将不同量纲的特征统一归一化成标准正态分布,可以进行统一比较。
#### 2, 计算协方差矩阵
协方差用于衡量两个变量之间的相关性,这个概念是在方差的基础上延伸而来,方差的定义如下
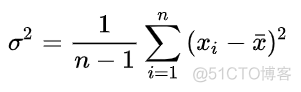
方差用于衡量变量偏移均值的程度,而协方差的公式如下
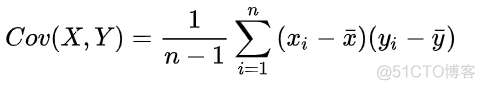
同时考虑了x和y两个变量偏移均值的程度,而且由于是相乘操作,所以当协方差的值大于0时,x和y的变化方向相同,小于0时,x和y的变化方向相反。因此,协方差的值可以反映两个变量之间的相关性,而且相关系数也就是在协方差的基础上除以两个变量的标准差得到的,pearson相关系数的公式如下
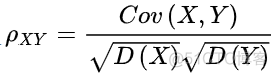
协方差矩阵就是多个变量两两之间协方差所构成的矩阵,以3个特征为例,对应的协方差矩阵如下
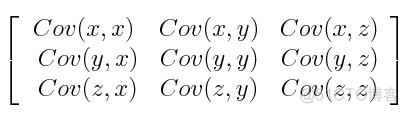
对于变量与自身的协方差,其值就是对应的方差了,所以在协方差矩阵中,对角线的值是各个变量的方差。
#### 3. 计算协方差矩阵的特征值和特征向量
这一步是PCA的核心,PCA中所谓的主成分就是特征值最大的特征向量了。所以首先计算特征值和特征向量。从这里看出,PCA降维之后的主成分,并不是原来输入的特征了,而是原始特征的线性组合。
#### 4. 选取topN主成分
将特征值按照从大到小排序,选取topN个特征向量,构成新的特征矩阵。
#### 5. 投影
将样本点投影到特征向量上,以二维数据为例,投影前的结果如下
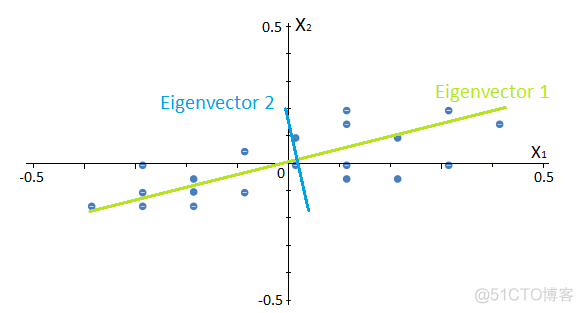
投影到特征向量之后的结果如下
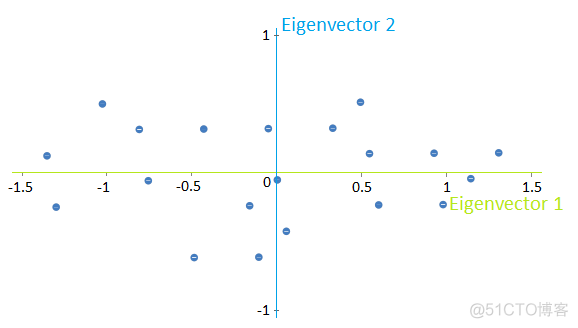
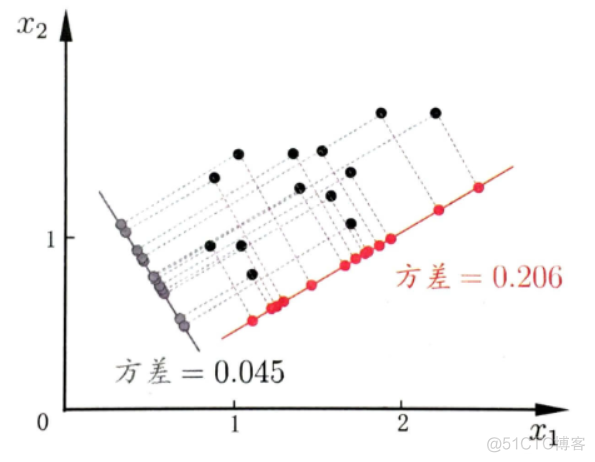
对于每一个主成分而言,有一个方差,这个值就是投影到该主成分之后的值对应的方差,示意如下
在筛选主成分的时候,我们会利用如下所示的碎石图
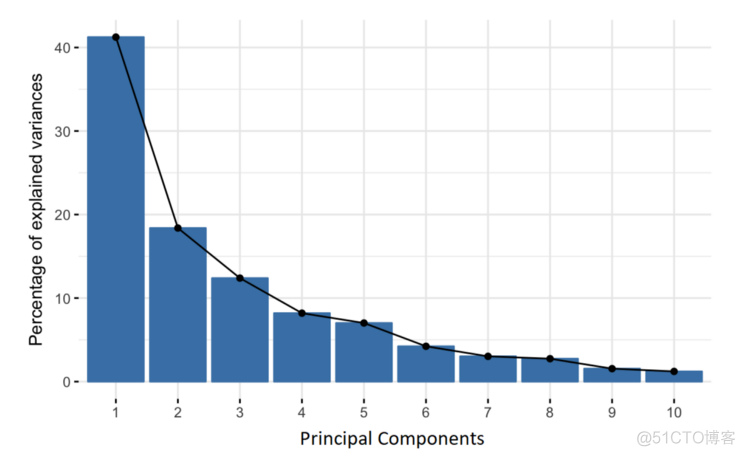
图中横坐标表示每个主成分,依次为PC1, PC2, 对应的方差值由大变小,通过判断折线图的拐点来筛选topN个主成分。
在scikit-learn中,进行PCA降维的代码如下
>>> from sklearn import datasets>>> from sklearn.decomposition import PCA
>>> iris = datasets.load_iris()
>>> X = iris.data
>>> y = iris.target
>>> pca = PCA(n_components=2)
>>> X_r = pca.fit(X).transform(X)
>>> pca.explained_variance_ratio_
array([0.92461872, 0.05306648])
可视化的代码如下
>>> import matplotlib.pyplot as plt>>> target_names = iris.target_names
>>> plt.figure()
<Figure size 640x480 with 0 Axes>
>>> colors = ['navy', 'turquoise', 'darkorange']
>>> lw = 2
>>> for color, i, target_name in zip(colors, [0, 1, 2], target_names):
... plt.scatter(X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=.8, lw=lw,
... label=target_name)
...
<matplotlib.collections.PathCollection object at 0x01894FD0>
<matplotlib.collections.PathCollection object at 0x018A31A8>
<matplotlib.collections.PathCollection object at 0x018A33B8>
>>> plt.legend(loc='best', shadow=False, scatterpoints=1)
<matplotlib.legend.Legend object at 0x018F8700>
>>> plt.title('PCA of IRIS dataset')
Text(0.5, 1.0, 'PCA of IRIS dataset')
>>> plt.show()
结果如下
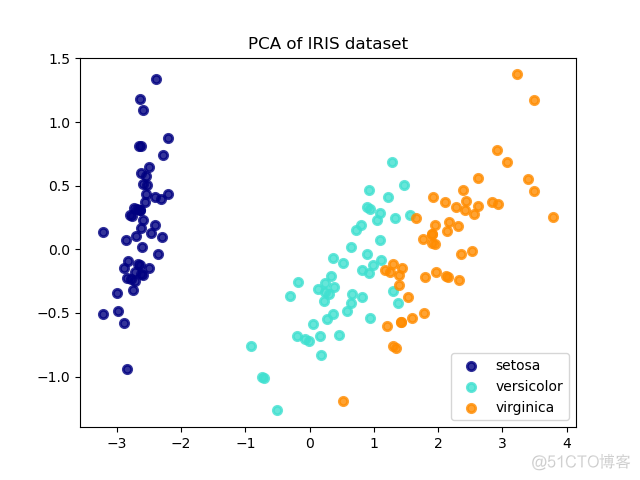
作为应用最广泛的降维算法,PCA方法计算简便,易于实现,但是解释性较差,因为新的主成分是原始特征的组合,无法与原始特征一一对应。
·end·

一个只分享干货的
生信公众号
