前言
今天在看ThreadPoolExecutor的介绍时,看到了它的workQueue中有一种优先任务队列,本质上是一个二叉堆(最多有2个孩子节点)。今天就来开始分析一下二叉堆这种数据结构
优先队列
和队列类似,但是出队的元素是优先级最高的元素。如下图所示,我们定义元素值越小,优先级越高。
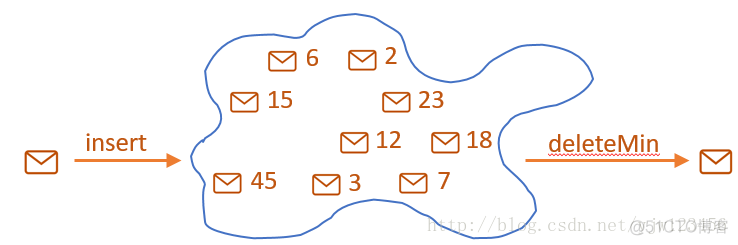
优先队列一般用二叉堆来实现。
完全二叉堆
完全二叉堆就结构性质上来说就是一个完全填满的二叉树,满足结构性和堆序性。
- 结构性
- 逻辑上,等同于完全二叉树
- 物理上,借助于向量(底层是数组)实现
- 堆序性
- 父节点的值总是大于或等于(小于或等于)任何一个子节点的值,且每个节点的左子树和右子树都是一个二叉堆。
若父节点的值总是大于(或等于)子节点的值,我们称这种堆为大顶堆;若总是小于(或等于)子节点的值,称为小顶堆。
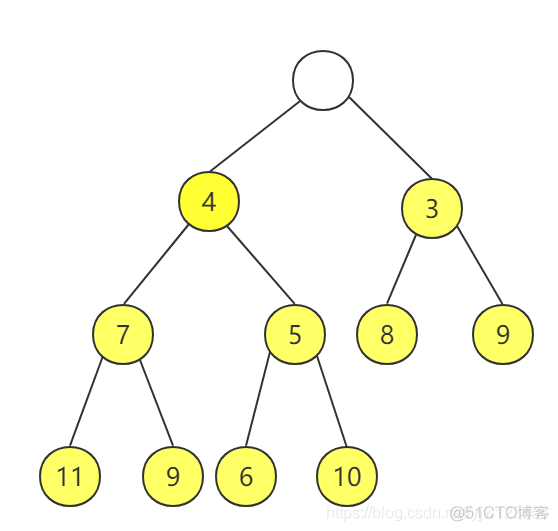
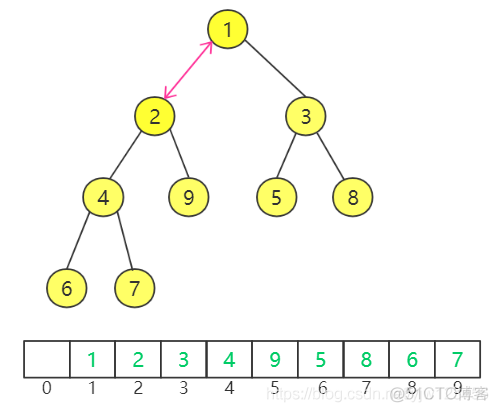
下图是一个小顶堆的示例图:
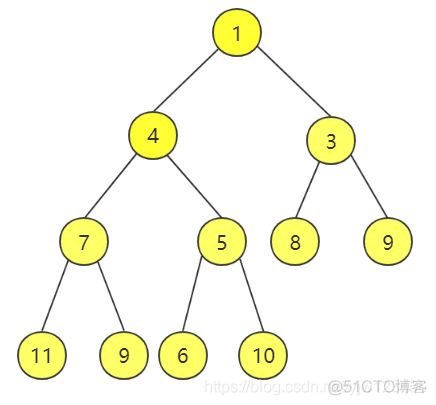
其对应的数组表示如下:

可以看到,与上面二叉树的层次遍历次序完全一致,我们定义第一个元素从下标1开始,因此0位置是没值的。
在这种表示下,很容易计算出下标为i的左孩子以及右孩子的位置(下标):
- 左孩子: 2 * i
- 右孩子:2 * i + 1
比如,节点5的下标为5(真的只是巧合),其左孩子下标为10,值为6;右孩子下标为11,值为10。
且上面的堆元素个数size为11,有孩子的节点满足2 * i <= size
插入
那么如果构造这样一颗完全二叉堆呢?先从插入开始了解
为了插入新节点,将新节点追加到数组最后的位置。这样做的好处是,可以使得结构性得以延续,若堆序性也能保持,则插入完成。
但是,通常情况下,新加入的节点会破坏堆序性。
并只是与其父节点违反堆序性,将其与父节点换位,若满足堆序性,则插入完成;否则继续与(新)父节点换位。
这样一种过程称为上滤。
假设,已存在一个这样的小顶堆,如何插入新节点2呢?
(为了好画图,把上图的10删除先…)
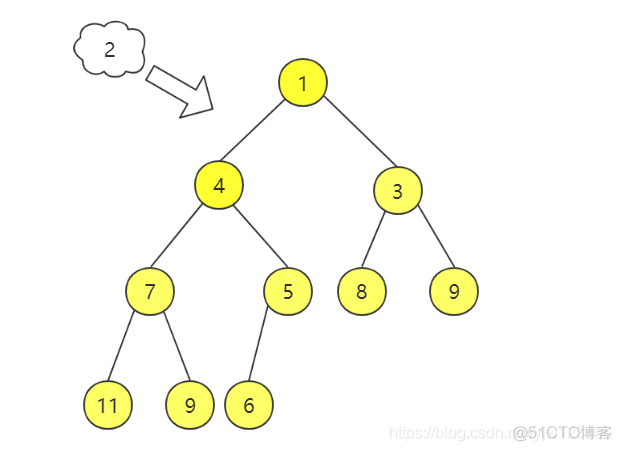
将新节点(节点2)放入堆的最后一个位置
然后执行向上过滤的操作:
- 如果小于父节点,则与父节点交换位置
- 重复直到大于父节点或者达到堆顶
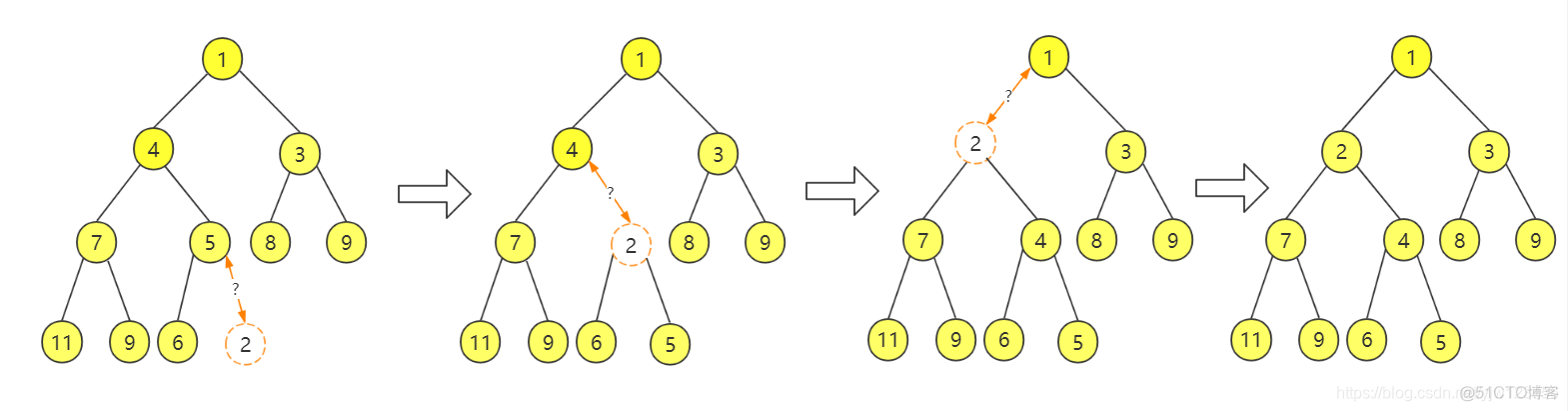
如上图所示,新加入的节点比父节点5小,交换;继续与新父节点4比较,交换;继续与新父节点1比较,不需要交换,插入完成。
删除
最小元素始终在堆顶,因此可以直接删除,但是这破坏了结构性。
为了保持结构性,通常的做法是,把最末元素移到堆顶上去。但是很有可能会破坏堆序性:
- 若新的节点与其子节点违反了堆序性,则
- 将新节点与其最小子节点换位
- 若交换后堆序性恢复,则完成;否则继续上一步操作
这个过程称为下滤。
下面通过图示来描述:
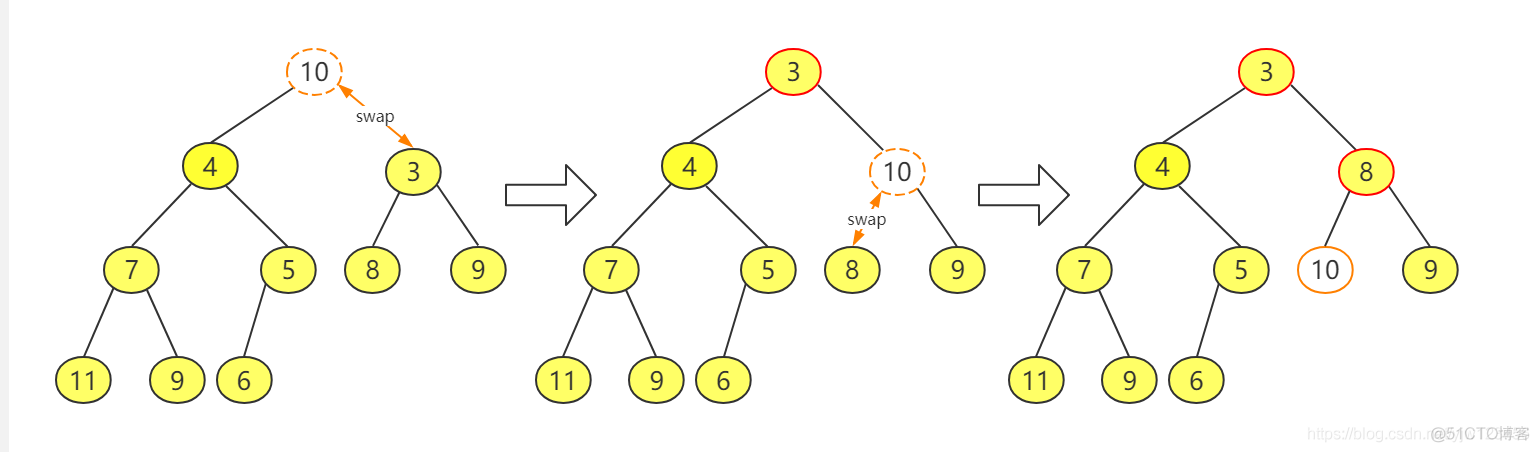
首先,删除掉堆顶后,把最末尾的元素移动到堆顶,形成上图堆1;此时破坏了堆序性,因此与最小的子节点3交换 ,上图堆2;
此时,可以看到还是不满足堆序性,继续与最小的子节点8交换,得到上图堆3,此时已经没有子节点了,并且满足了堆序性,操作完成。
批量建堆
回顾删除算法,任意给定堆h1和h2,以及节点p。
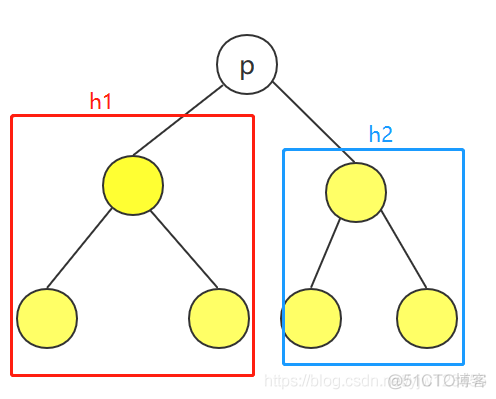
其中堆h1和h2是满足堆序性和结构性的完全二叉堆,为了得到h1和h2以及节点p组成的新堆,
只需将h1和h2当成p的子堆,对p进行下滤,这样就能得到想要的新堆。
基于这个思想,我们自下而上、自右而左,依次下滤每个内部节点(不包括叶子节点,叶子节点也不能下滤了),
这种操作可理解为子堆的逐层向上合并。
public void testBuildHeap() {
List<Integer> list = IntStream.range(1,10).boxed().collect(Collectors.toList());
Collections.shuffle(list);
System.out.println(list);//[2, 6, 8, 7, 9, 5, 3, 4, 1]
BinaryHeap<Integer> heap = new BinaryHeap<>(list.toArray(new Integer[]{}));
System.out.println(heap);//[1, 2, 3, 4, 9, 5, 8, 6, 7]
}
通过程序生成1-9的9个数字,然后进行洗牌操作。我们利用这个随机生成的数组来讲解
批量建堆操作:
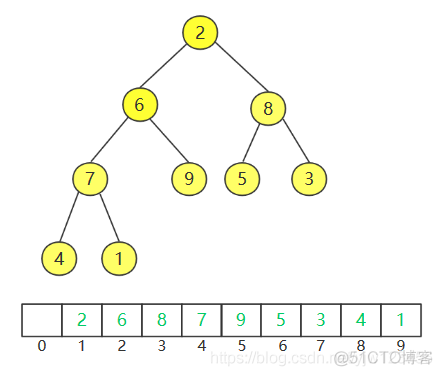
首先按照层次遍历的顺序构建一个堆,同样舍弃索引为0的位置。可以看到,结构性满足,但是堆序性是不满足的,为啥,最小的1都到了最下面了。
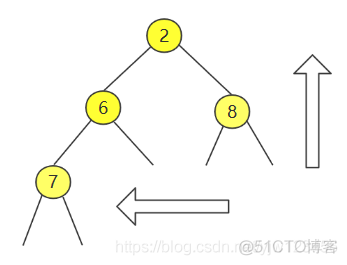
上图所示是所有的内部节点,我们按照自下而上、自右而左的顺序,依次下滤每个内部节点。首先下滤最后一个内部节点,9/2=4 对应的值为7,这里我们详细说一下,其左右孩子都是只有一个节点的堆,因此,一个节点的堆满足完全二叉堆的条件。对7进行下滤:
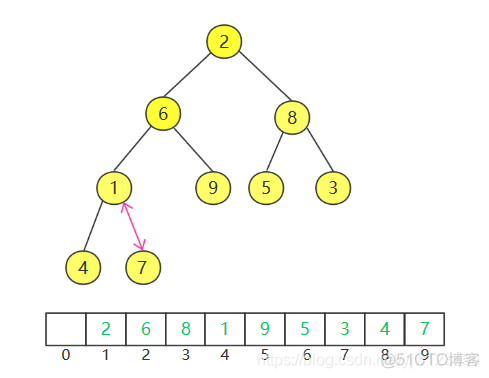
接下来是值为8的节点:
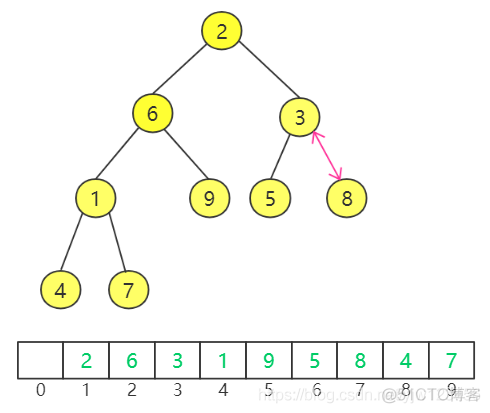
按照顺序,然后是值为6的节点,注意这里交换了两次(6<->1,6<->4),为了简单我就没把每一步都画出来了:
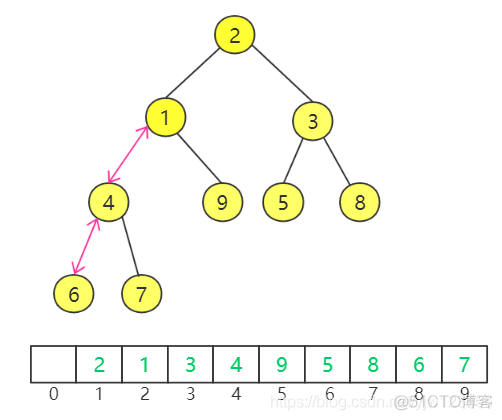
最后是值为2的节点,先不着急,我们回顾一下,这个算法有一个特点是,已经处理的左右节点都保持了完全二叉堆的特性。然后对2进行下滤操作,1、3中最小的是1,因此2与1换位:
代码
package com.algorithms.heap;/**
* 堆是一颗完全填满的二叉树,底层可能未被填满,但是元素是从左到右填入的,这样的树称为完成二叉树。
* <p>
* 小顶堆:最小元素在根上,任意子树也要满足这个性质。这里
*
* @author yjw
* @date 2019/4/23/023
*/
@SuppressWarnings("unchecked")
public class BinaryHeap<E extends Comparable<? super E>> implements Heap<E> {
/**
* 堆中元素数
*/
private int size = 0;
/**
* 索引为0的位置不存任何元素
*/
private E[] array;
public BinaryHeap() {
this(DEFAULT_CAPACITY);
}
public BinaryHeap(int capacity) {
array = (E[]) new Comparable[capacity + 1];
}
public BinaryHeap(E[] items) {
size = items.length;
array = (E[]) new Comparable[(size + 2) * 11/10];
int i = 1;//第一元素
for (E item : items) {
array[i++] = item;
}
buildHeap();
}
public BinaryHeap(Iterable<E> items) {
this();
items.forEach(this::insert);
}
/**
* 构建堆
* 通过size/2次下滤操作构建堆
*/
private void buildHeap() {
for (int i = size / 2; i > 0 ; i--) {
percolateDown(i);
}
}
@Override
public void insert(E x) {
if (size == array.length - 1) {
ensureCapacity(array.length * 2 + 1);
}
int hole = ++size;
array[0] = x;//必须设置array[0],否则循环跳不出,或报空指针
while (x.compareTo(array[hole/2]) < 0) {
//往上冒
array[hole] = array[hole/2];
hole = hole/2;
}
array[hole] = x;
}
/**
* 扩容
* @param newCapacity
*/
private void ensureCapacity(int newCapacity) {
E[] oldArray = array;
array = (E[]) new Comparable[newCapacity];
for (int i = 1; i < oldArray.length; i++) {
array[i] = oldArray[i];
}
}
@Override
public E findMin() {
return array[1];
}
@Override
public E deleteMin() {
if (isEmpty()) {
throw new IllegalArgumentException();
}
E min = findMin();//缓存最小元素
array[1] = array[size--];//用最后一个元素替代最小元素的位置,此时最小元素已经被覆盖了,但是我们通过min变量缓存起来了
percolateDown(1);//进行下滤操作
return min;
}
/**
* 下滤操作
* 由于是小顶堆,每次取孩子中最小的元素替换父节点的位置
* @param hole 待下滤的节点位置
*/
private void percolateDown(int hole) {
int child;
E tmp = array[hole];
while (hole * 2 <= size) {
//如果有孩子,hole不停的往下,直到不满足堆的性质
child = hole * 2;
//若有右孩子,且右孩子更小
if (child != size &&
array[child +1].compareTo(array[child]) < 0) {
child++;//取右孩子
}
if (array[child].compareTo(tmp) < 0) {
//hole位置填充最小孩子节点的值
array[hole] = array[child];
hole = child;//继续比较
} else {
break;
}
}
array[hole] = tmp;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public void makeEmpty() {
for (int i = 1; i <=size; i++) {
array[i] = null;
}
size = 0;
}
}
Heap接口代码:
public interface Heap<E> {int DEFAULT_CAPACITY = 10;
void insert(E x);
E findMin();
E deleteMin();
boolean isEmpty();
void makeEmpty();
}
