1 内容介绍
在本文中,我们为大规模多用户 (MU) 多输入多输出 (MIMO) 无线系统提出了一种新颖的数据检测算法和相应的 VLSI 设计。我们的算法使用基于交替方向乘法器 (ADMM) 的无限范数约束均衡,称为 ADMIN。ADMIN 是一种迭代算法,当基站 (BS) 和用户天线的数量之比较小时,它的性能大大优于线性检测器。在第一次迭代中,ADMIN 计算线性最小均方误差 (MMSE) 解,这在 BS 和用户天线数量之比较大时就足够了。我们为支持 16 和 32 用户系统的基于 LDL 分解的软输出 ADMIN 开发分时和迭代 VLSI 架构。我们提出了用于 28-nm CMOS 中的 16-64 个天线基站的专用集成电路 (ASIC) 设计,支持多达 64 个正交幅度调制 (QAM)。16 用户 ADMIN ASIC 达到 303 Mb/s,同时耗散 85 mW。
2 部分代码
% -----------------------------------------------------
% -- Simulation of state-of-the-art massive MIMO detection algorithms
% -- Author: Shahriar Shahabuddin
% -- Email: shahriar.cwc@gmail.com
% This simulator is based on Christoph Studer's simple MIMO simulator. This
% simulator contains the following algorithms:
% (1) Conventional detection schemes: matched filtering, MMSE, SIMO
% (2) Approximate Inversion Based Detection: neumann-series approximation,
% gauss-seidel detection, conjugate-gradient detection
% (3) BOX detection based methods: ADMIN, OCD
%
% Please cite the following paper if you use this simulator,
% S. Shahabddin, M. Juntti and C. Studer, "ADMM-based infinity-norm
% detector for large-scale MIMO", IEEE International symposium of circuits
% and systems, Maryland, USA, May 2017.
% -----------------------------------------------------
function massiveMIMOdetectors(varargin)
% -- set up default/custom parameters
close all
if isempty(varargin)
disp('using default simulation settings and parameters...')
% set default simulation parameters
par.suffix = 'exp'; % simulation name suffix: 'exp' experimental
par.runId = 0; % simulation ID (used to reproduce results)
par.MR = 64; % receive antennas
par.MT = 16; % user terminals (set not larger than MR!)
par.mod = '64QAM'; % modulation type: 'BPSK','QPSK','16QAM','64QAM'
par.simName = ['ERR_' num2str(par.MR) 'x' num2str(par.MT) '_' par.mod '_' par.suffix] ; % simulation name (used for saving results)
par.trials = 100; % number of Monte-Carlo trials (transmissions)
par.SNRdB_list = 10:2:20; % list of SNR [dB] values to be simulated
par.detector = {'Conjugate-Gradient','Neumann','Gauss-Seidel','OCDBOX','ADMIN'}; % define detector(s) to be simulated
% algorithm specific
par.alg.maxiter = 3;
else
disp('use custom simulation settings and parameters...')
par = varargin{1}; % only argument is par structure
end
% -- initialization
% use runId random seed (enables reproducibility)
% rng(par.runId);
% set up Gray-mapped constellation alphabet (according to IEEE 802.11)
switch (par.mod)
case 'BPSK'
par.symbols = [ -1 1 ];
case 'QPSK'
par.symbols = [ -1-1i,-1+1i, ...
+1-1i,+1+1i ];
case '16QAM'
par.symbols = [ -3-3i,-3-1i,-3+3i,-3+1i, ...
-1-3i,-1-1i,-1+3i,-1+1i, ...
+3-3i,+3-1i,+3+3i,+3+1i, ...
+1-3i,+1-1i,+1+3i,+1+1i ];
case '64QAM'
par.symbols = [ -7-7i,-7-5i,-7-1i,-7-3i,-7+7i,-7+5i,-7+1i,-7+3i, ...
-5-7i,-5-5i,-5-1i,-5-3i,-5+7i,-5+5i,-5+1i,-5+3i, ...
-1-7i,-1-5i,-1-1i,-1-3i,-1+7i,-1+5i,-1+1i,-1+3i, ...
-3-7i,-3-5i,-3-1i,-3-3i,-3+7i,-3+5i,-3+1i,-3+3i, ...
+7-7i,+7-5i,+7-1i,+7-3i,+7+7i,+7+5i,+7+1i,+7+3i, ...
+5-7i,+5-5i,+5-1i,+5-3i,+5+7i,+5+5i,+5+1i,+5+3i, ...
+1-7i,+1-5i,+1-1i,+1-3i,+1+7i,+1+5i,+1+1i,+1+3i, ...
+3-7i,+3-5i,+3-1i,+3-3i,+3+7i,+3+5i,+3+1i,+3+3i ];
end
% extract average symbol energy
par.Es = mean(abs(par.symbols).^2);
% precompute bit labels
par.Q = log2(length(par.symbols)); % number of bits per symbol
par.bits = de2bi(0:length(par.symbols)-1,par.Q,'left-msb');
% track simulation time
time_elapsed = 0;
% -- start simulation
% initialize result arrays (detector x SNR)
res.VER = zeros(length(par.detector),length(par.SNRdB_list)); % vector error rate
res.SER = zeros(length(par.detector),length(par.SNRdB_list)); % symbol error rate
res.BER = zeros(length(par.detector),length(par.SNRdB_list)); % bit error rate
% generate random bit stream (antenna x bit x trial)
bits = randi([0 1],par.MT,par.Q,par.trials);
% trials loop
tic
for t=1:par.trials
% generate transmit symbol
idx = bi2de(bits(:,:,t),'left-msb')+1;
s = par.symbols(idx).';
% generate iid Gaussian channel matrix & noise vector
n = sqrt(0.5)*(randn(par.MR,1)+1i*randn(par.MR,1));
H = sqrt(0.5)*(randn(par.MR,par.MT)+1i*randn(par.MR,par.MT));
% transmit over noiseless channel (will be used later)
x = H*s;
% SNR loop
for k=1:length(par.SNRdB_list)
% Current SNR point in dBs
SNR_dB = par.SNRdB_list(k);
% Linear SNR
SNR_lin = 10.^(SNR_dB./10);
% Variance of complex noise per receive antenna
N0 = par.Es*par.MT/SNR_lin;
% transmit data over noisy channel
y = x+sqrt(N0)*n;
% algorithm loop
for d=1:length(par.detector)
switch (par.detector{d}) % select algorithms
case 'MF' % Matched Filter
[idxhat,bithat] = MF(par,H,y,N0);
case 'MMSE' % MMSE detector
[idxhat,bithat] = MMSE(par,H,y,N0);
case 'SIMO' % SIMO lower bound
[idxhat,bithat] = SIMO(par,H,y,N0,s);
case 'ADMIN' % ADMM-based Infinity Norm detector
[idxhat,bithat] = ADMIN(par,H,y,N0);
case 'OCDBOX' % co-ordinate descent (optimized) detector
[idxhat,bithat] = OCDBOX(par,H,y);
case 'Neumann' % coordinate descent
[idxhat,bithat] = Neumann(par,H,y,N0);
case 'Gauss-Seidel' % Gauss-Seidel detector
[idxhat,bithat] = Gauss_Seidel(par,H,y,N0);
case 'Conjugate-Gradient' % conjugate gradient detector
[idxhat,bithat] = CG(par,H,y,N0);
otherwise
error('par.detector type not defined.')
end
% -- compute error metrics
err = (idx~=idxhat);
res.VER(d,k) = res.VER(d,k) + any(err);
res.SER(d,k) = res.SER(d,k) + sum(err)/par.MT;
res.BER(d,k) = res.BER(d,k) + sum(sum(bits(:,:,t)~=bithat))/(par.MT*par.Q);
end % algorithm loop
end % SNR loop
% keep track of simulation time
if toc>10
time=toc;
time_elapsed = time_elapsed + time;
fprintf('estimated remaining simulation time: %3.0f min.\n',time_elapsed*(par.trials/t-1)/60);
tic
end
end % trials loop
% normalize results
res.VER = res.VER/par.trials;
res.SER = res.SER/par.trials;
res.BER = res.BER/par.trials;
res.time_elapsed = time_elapsed;
% -- save final results (par and res structure)
% save([ par.simName '_' num2str(par.runId) ],'par','res');
% -- show results (generates fairly nice Matlab plot)
marker_style = {'bo-','rs--','mv-.','kp:','g*-','c>--','yx:'};
figure(1)
for d=1:length(par.detector)
if d==1
semilogy(par.SNRdB_list,res.BER(d,:),marker_style{d},'LineWidth',2)
hold on
else
semilogy(par.SNRdB_list,res.BER(d,:),marker_style{d},'LineWidth',2)
end
end
hold off
grid on
xlabel('average SNR per receive antenna [dB]','FontSize',12)
ylabel('bit error rate (BER)','FontSize',12)
axis([min(par.SNRdB_list) max(par.SNRdB_list) 1e-4 1])
legend(par.detector,'FontSize',12)
set(gca,'FontSize',12)
end
% -- set of detector functions
%% Matched filter
function [idxhat,bithat] = MF(par,H,y)
xhat = H' * y / norm(H(:));
[~,idxhat] = min(abs(xhat*ones(1,length(par.symbols))-ones(par.MT,1)*par.symbols).^2,[],2);
bithat = par.bits(idxhat,:);
end
%% MMSE detector (MMSE)
function [idxhat,bithat] = MMSE(par,H,y,N0)
xhat = (H'*H+(N0/par.Es)*eye(par.MT))\(H'*y);
[~,idxhat] = min(abs(xhat*ones(1,length(par.symbols))-ones(par.MT,1)*par.symbols).^2,[],2);
bithat = par.bits(idxhat,:);
end
%% SIMO bound
function [idxhat,bithat] = SIMO(par,H,y,s)
z = y-H*s;
xhat = zeros(par.MT,1);
for m=1:par.MT
hm = H(:,m);
yhat = z+hm*s(m,1);
xhat(m,1) = hm'*yhat/norm(hm,2)^2;
end
[~,idxhat] = min(abs(xhat*ones(1,length(par.symbols))-ones(par.MT,1)*par.symbols).^2,[],2);
bithat = par.bits(idxhat,:);
end
%% Neumann-Series Approximation based massive MIMO detection
function [idxhat,bithat] = Neumann(par,H,y,N0)
A = H'*H+(N0/par.Es)*eye(par.MT);
MF = H'*y;
D = diag(diag(A));
E = triu(A,1)+tril(A,-1);
Ainv = 0;
for i = 0:par.alg.maxiter
Ainv = Ainv+((-inv(D)*E)^i)*inv(D);
end
xhat = Ainv*MF;
[~,idxhat] = min(abs(xhat*ones(1,length(par.symbols))-ones(par.MT,1)*par.symbols).^2,[],2);
bithat = par.bits(idxhat,:);
end
%% Gauss-Seidel massive MIMO detection
function [idxhat,bithat] = Gauss_Seidel(par,H,y,N0)
A = H'*H+(N0/par.Es)*eye(par.MT);
MF = H'*y;
D = diag(diag(A));
E = -triu(A,1);
F = -tril(A,-1);
xhat = diag(inv(D));% inv(D)*MF; %%% Check Gauss Seidel detection paper
for i = 0:par.alg.maxiter
xhat = inv(D-E)*(F*xhat+MF);
end
[~,idxhat] = min(abs(xhat*ones(1,length(par.symbols))-ones(par.MT,1)*par.symbols).^2,[],2);
bithat = par.bits(idxhat,:);
end
%% Conjugate Gradient massive MIMO detection
function [idxhat,bithat] = CG(par,H,y,N0)
A = H'*H+(N0/par.Es)*eye(par.MT);
MF = H'*y;
r = MF;
p = r;
v = zeros(par.MT,1);
for k = 1:par.alg.maxiter
e = A*p;
alpha = norm(r)^2/(p'*e);
v = v+alpha*p;
new_r = r-alpha*e;
beta = norm(new_r)^2/norm(r)^2;
p = new_r+beta*p;
r = new_r;
end
xhat = v;
[~,idxhat] = min(abs(xhat*ones(1,length(par.symbols))-ones(par.MT,1)*par.symbols).^2,[],2);
bithat = par.bits(idxhat,:);
end
%% ADMM-based infinity norm (ADMIN) detector
function [idxhat,bithat] = ADMIN(par,H,y,N0)
% -- preprocessing
% by setting beta to N0/par.Es we get the MMSE estimator in the first iteration
% this is pretty neat as this is a very good detector already
beta = N0/par.Es;%*3; % tweaking this one by 3 improved performance significantly
A = H'*H + beta*eye(par.MT);
L = chol(A,'lower');
yMF = H'*y;
% -- initialization
gamma = (1+sqrt(5))/2;%*2; %% tweaked with 2 to improve performance
alpha = max(real(par.symbols)); % symbol box
zhat = zeros(par.MT,1);
lambda = zeros(par.MT,1);
% -- ADMM loop
for iter=1:par.alg.maxiter
xhat = (L')\(L\(yMF+beta*(zhat-lambda))); % step 1
zhat = projinf(par,xhat+lambda,alpha); % step 2
lambda = lambda-real(gamma*(zhat-xhat)); % step 3
lambda = real(lambda);
end
% -- hard output detection
[~,idxhat] = min(abs(zhat*ones(1,length(par.symbols))-ones(par.MT,1)*par.symbols).^2,[],2);
bithat = par.bits(idxhat,:);
end
%% Optimized Coordinate Descent (OCD) BOX version
function [idxhat,bithat] = OCDBOX(par,H,y)
% -- initialization
[row, col] = size(H);
alpha = 0; % no regularization for BOX detector
beta = max(real(par.symbols));
% -- preprocessing
dinv = zeros(col,1);
p = zeros(col,1);
for uu=1:col
normH2 = norm(H(:,uu),2)^2;
dinv(uu,1) = 1/(normH2+alpha);
p(uu,1) = dinv(uu)*normH2;
end
r = y;
zold = zeros(col,1);
znew = zeros(col,1);
deltaz = zeros(col,1);
% -- OCD loop
for iters=1:par.alg.maxiter
for uu=1:col
tmp = dinv(uu)*(H(:,uu)'*r)+p(uu)*zold(uu);
znew(uu) = projinf(par,tmp,beta);
deltaz(uu) = znew(uu)-zold(uu);
r = r - H(:,uu)*deltaz(uu);
zold(uu) = znew(uu);
end
end
[~,idxhat] = min(abs(znew*ones(1,length(par.symbols))-ones(par.MT,1)*par.symbols).^2,[],2);
bithat = par.bits(idxhat,:);
end
% project onto alpha infinity-tilde-norm ball
function sproj = projinf(par,s,alpha)
switch par.mod
case 'BPSK'
v = real(s);
sproj = min(abs(v),alpha).*v;
otherwise
sr = real(s);
idxr = abs(sr)>alpha;
sr(idxr) = sign(sr(idxr))*alpha;
si = imag(s);
idxi = abs(si)>alpha;
si(idxi) = sign(si(idxi))*alpha;
sproj = sr +1i*si;
end
end
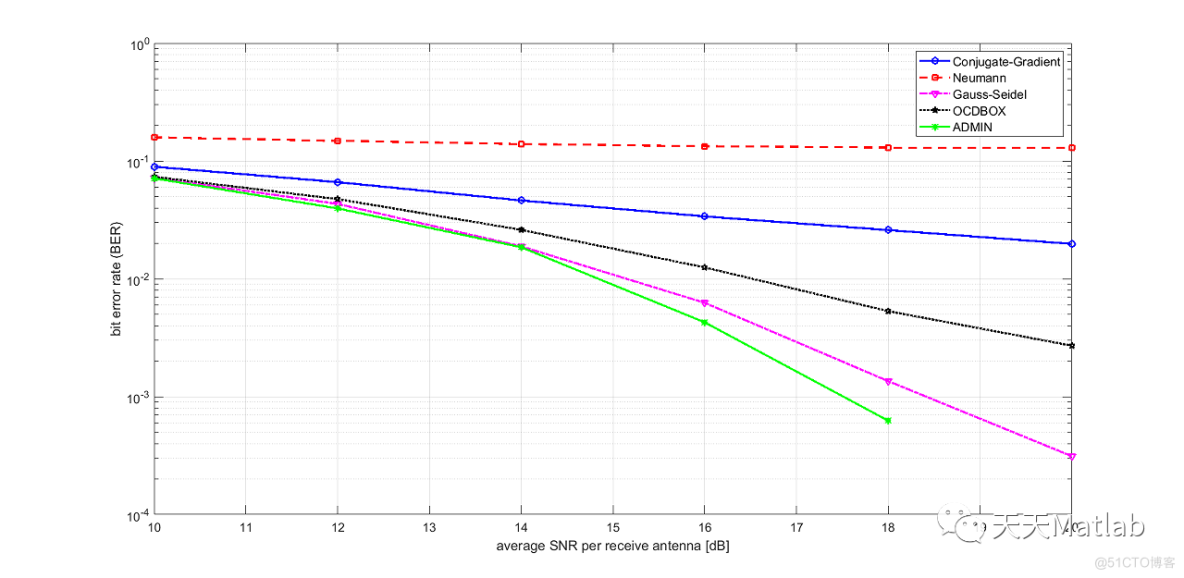
3 运行结果
4 参考文献
[1] Shahabuddin S , Hautala I , Juntti M , et al. ADMM-Based Infinity-Norm Detection for Massive MIMO: Algorithm and VLSI Architecture[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2021, PP(99):1-13.
