1 内容介绍
针对鸡群算法因小鸡粒子易陷入局部最优而无法取得全局最优解问题,在小鸡粒子位置更新中加入自身惯性权重和向子群中公鸡粒子学习部分,提出具有随机惯性权重和固定学习因子的改进鸡群算法,然后用模拟退火算法对改进鸡群算法陷入停滞状态时已得到的最优解进行邻域搜索,使算法具有跳出局部最优取得全局最优解的能力,最后将基于模拟退火的改进鸡群算法用于4个标准测试函数寻优.仿真结果表明,基于模拟退火的改进鸡群算法全局搜索能力强,收敛速度快,精度高,与粒子群算法,鸡群算法以及改进鸡群算法相比寻优性能更佳.
2 部分代码
% -----------------------------------------------------------------------------------------------------------
% Chicken Swarm Optimization (CSO) (demo)
% Programmed by Xian-bing Meng
% Updated 25 Aug, 2014.
%
% This is a simple demo version only implemented the basic
% idea of the CSO for solving the unconstrained problem, namely Sphere function.
% The details about CSO are illustratred in the following paper.
% (Citation details):
% Xian-bing Meng, Xiao-zhi Gao., A new bio-inspired algorithm: Chicken Swarm Optimization
% in: ICSI 2014, Part I, LNCS 8794, pp. 86-94
% Email: x.b.meng12@gmail.com; xiao-zhi.gao@aalto.fi
%
% The parameters in CSO are presented as follows.
% fitness % The fitness function
% M % Maxmimal generations (iterations)
% pop % Population size
% dim % Number of dimensions
% G % How often the chicken swamr can be updated.
% rPercent % The population size of roosters accounts for "rPercent" percent of the total population size
% hPercent % The population size of hens accounts for "hPercent" percent of the total population size
% mPercent % The population size of mother hens accounts for "mPercent" percent of the population size of hens
%
% Using the default value, you can execute this algorithm using the following code.
% [ bestX, fMin ] = CSO
% -----------------------------------------------------------------------------------------------------------
% Main programs starts here
function [ bestX, fMin ] = CSO( fitness, M, pop, dim, G, rPercent, hPercent, mPercent )
% Display help
help CSO.m
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% set the parameter values
if nargin < 1
Func = @Sphere;
M = 1000; % Maxmimal generations (iterations)
pop = 100; % Population size
dim = 20; % Number of dimensions
G = 10; % How often the chicken swamr can be updated. The details of its meaning are illustrated at the following codes.
rPercent = 0.2; % The population size of roosters accounts for "rPercent" percent of the total population size
hPercent = 0.6; % The population size of hens accounts for "hPercent" percent of the total population size
mPercent = 0.1; % The population size of mother hens accounts for "mPercent" percent of the population size of hens
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
rNum = round( pop * rPercent ); % The population size of roosters
hNum = round( pop * hPercent ); % The population size of hens
cNum = pop - rNum - hNum; % The population size of chicks
mNum = round( hNum * mPercent ); % The population size of mother hens
lb= -100*ones( 1,dim ); % Lower limit/bounds/ a vector
ub= 100*ones( 1,dim ); % Upper limit/bounds/ a vector
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Initialization
for i = 1 : pop
x( i, : ) = lb + (ub - lb) .* rand( 1, dim ); % The position of the i (th) chicken
fit( i ) = Func( x( i, : ) ); % The fitness value of the i (th) chicken
end
pFit = fit; % The individual's best fitness value
pX = x; % The individual's best position corresponding to the pFit
[ fMin, bestI ] = min( fit ); % fMin denotes the global optimum fitness value
bestX = x( bestI, : ); % bestX denotes the global optimum position corresponding to fMin
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Start updating the solutions.
for t = 1 : M
% This parameter is to describe how the chicks would follow their mother to forage for food.
FL = rand( pop, 1 ) .* 0.4 + 0.5; % In fact, there exist cNum chicks, thus only cNum values of FL would be used.
%Note that cNum may be dynamically changed!
% The hierarchal order, dominance relationship, mother-child relationship, the roosters, hens and the chicks in a
% group will remain unchanged. These statuses are only updated every several ( G) time steps.
% In fact, this parameter G is used to simulate the situation that the chicken swarm have been changed, including that some
% chickens have died, or the chicks have grown up and became roosters or hens,
% or some mother hens have hatched new offspring (chicks) and so on.
if( mod( t, G ) == 1 )
sortIndex = ones( pop, 1 ) .* ( pop + 1 ); % Initialize the sortIndex, the values of which would be anything valid.
% Except the ones that are the indexs of the chicken, such as 1,2,3,……pop.
[ ans, sortIndex ] = sort( fit ); % Here ans would be unused. Only sortIndex is useful.
% Note that how the chicken swarm can be divided into several groups and the identity
% of the chickens (roosters, hens and chicks) can be determined all depend on the fitness values of the
% chickens themselves. Hence we use " sortIndex( i ) " to describe the
% chicken, not the index " i " itself.
motherLib = randperm( hNum, mNum ) + rNum; % Randomly select which mNum hens would be the mother hens.
% We assume that all roosters are stronger than the hens, likewise, hens are stronger than the chicks.
% In CSO, the strong is reflected by the good fitness value. If the
% optimization problems is minimal ones, the more strong ones
% correspond to the ones with lower fitness values.
% Hence 1 : rNum chickens all belong to roosters.
% In turn, (rNum + 1) : (rNum + 1 + hNum ) belong to hens, .....chicks
% Here motherLib include all the mother hens.
% motherLib is the abbreviation of "mother library".
% Given the fact the 1 : rNum chickens' fitness values maybe not
% the best rNum ones.
% Thus we use sortIndex( 1 : rNum ) to describe the roosters.
mate = randi( rNum, hNum, 1 ); % randomly select each hen's mate, rooster.
% In fact, we can determine which group each hen inhabit using "mate"
% Each rooster stands for a group.For simplicity, we assume that
% there exist only one rooster in each group.
mother = motherLib( randi( mNum, cNum, 1 ) ); % randomly select cNum chicks' mother hens
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i = 1 : rNum % Update the rNum roosters' values.
anotherRooster = randiTabu( 1, rNum, i, 1 ); % randomly select another rooster different from the i (th) chicken.
if( pFit( sortIndex( i ) ) <= pFit( sortIndex( anotherRooster ) ) )
tempSigma = 1;
else
tempSigma = exp( ( pFit( sortIndex( anotherRooster ) ) - pFit( sortIndex( i ) ) ) / abs( pFit( sortIndex( i ) ) + 1e-50 ) );
end
x( sortIndex( i ), : ) = pX( sortIndex( i ), : ) .* ( 1 + tempSigma .* randn( 1, dim ) );
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = Func( x( sortIndex( i ), : ) );
end
for i = ( rNum + 1 ) : ( rNum + hNum ) % Update the hNum hens' values.
other = randiTabu( 1, i, mate( i - rNum ), 1 ); % randomly select another chicken different from the i (th) chicken's mate.
% Note that the "other" chicken's fitness value should be superior
% to that of the i (th) chicken. This means the i (th) chicken may steal
% the better food found by the "other" (th) chicken.
c1 = exp( ( pFit( sortIndex( i ) ) - pFit( sortIndex( mate( i - rNum ) ) ) ) / abs( pFit( sortIndex( i ) ) + 1e-50 ) );
c2 = exp( ( -pFit( sortIndex( i ) ) + pFit( sortIndex( other ) ) ) );
x( sortIndex( i ), : ) = pX( sortIndex( i ), : ) + ( pX( sortIndex( mate( i - rNum ) ), : ) - pX( sortIndex( i ), : ) ) .* c1 .* rand( 1, dim ) +...
( pX( sortIndex( other ), : ) - pX( sortIndex( i ), : ) ) .* c2 .* rand( 1, dim );
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = Func( x( sortIndex( i ), : ) );
end
for i = ( rNum + hNum + 1 ) : pop % Update the cNum chicks' values.
x( sortIndex( i ), : ) = pX( sortIndex( i ), : ) + ( pX( sortIndex( mother( i - rNum - hNum ) ), : ) - pX( sortIndex( i ), : ) ) .* FL( i );
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = Func( x( sortIndex( i ), : ) );
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Update the individual's best fitness vlaue and the global best fitness value
for i = 1 : pop
if ( fit( i ) < pFit( i ) )
pFit( i ) = fit( i );
pX( i, : ) = x( i, : );
end
if( pFit( i ) < fMin )
fMin = pFit( i );
bestX = pX( i, : );
end
end
end
% End of the main program
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% The following functions are associated with the main program
%---------------------------------------------------------------------------------------------------------------------------
% Note that this function is the objective function
function y = Sphere( x )
y = sum( x .^ 2 );
% Application of simple limits/bounds
function s = Bounds( s, Lb, Ub)
% Apply the lower bound vector
temp = s;
I = temp < Lb;
temp(I) = Lb(I);
% Apply the upper bound vector
J = temp > Ub;
temp(J) = Ub(J);
% Update this new move
s = temp;
%---------------------------------------------------------------------------------------------------------------------------
% Note that this function generate "dim" values, all of which are
% different from the value of "tabu"
function value = randiTabu( min, max, tabu, dim )
value = ones( dim, 1 ) .* max .* 2;
num = 1;
while ( num <= dim )
temp = randi( [min, max], 1, 1 );
if( length( find( value ~= temp ) ) == dim && temp ~= tabu )
value( num ) = temp;
num = num + 1;
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
3 运行结果
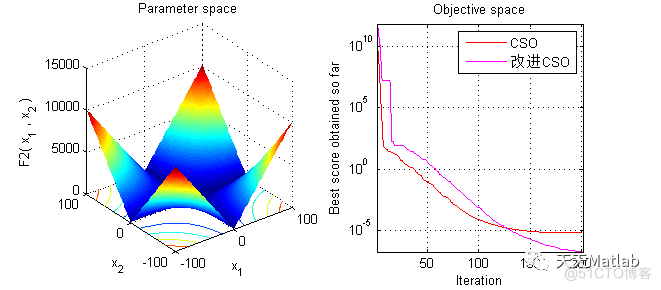
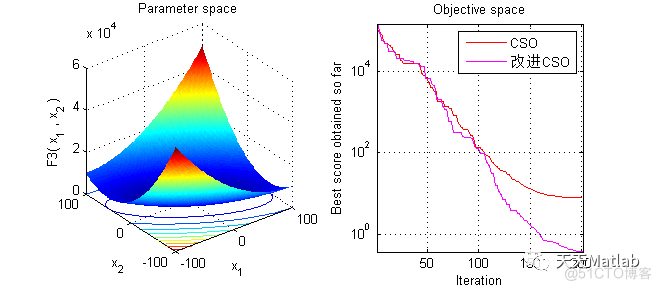
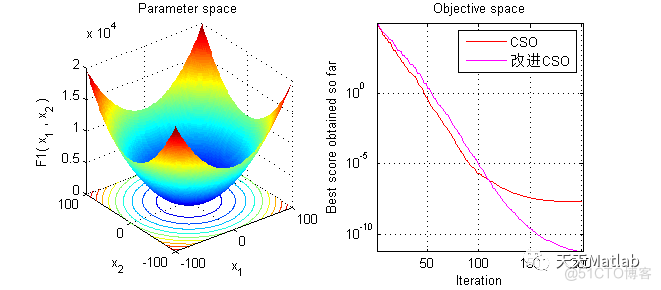
4 参考文献
[1]李振璧, 王康, 姜媛媛. 基于模拟退火的改进鸡群优化算法[J]. 微电子学与计算机, 2017, 34(2):5.
