目录
- 1. 前言
- 2. 压缩对称矩阵
- 3. 压缩稀疏矩阵
- 3.1 三元组表
- 3.2 以列优先搜索
- 3.3 找出存储位置
- 4. 总结
1. 前言
什么是特殊矩阵?
C++,一般使用二维数组存储矩阵数据。
在实际存储时,会发现矩阵中有许多值相同的数据或有许多零数据,且分布呈现出一定的规律,称这类型的矩阵为特殊矩阵。
为了节省存储空间,可以设计算法,对这类特殊矩阵进行压缩存储,让多个相同的非零数据只分配一个存储空间;对零数据不分配空间。
本文将讲解如何压缩这类特殊矩阵,以及压缩后如何保证矩阵的常规操作不受影响。
2. 压缩对称矩阵
什么是对称矩阵?
在一个n阶矩阵A中,若所有数据满足如下述特性,则可称A为对称矩阵。
a[i][j]==a[j][i]
i是数据在矩阵中的行号。
j是数据在矩阵中的列号。
0<<i,j<<n-1
在n阶对称矩阵 a[i][j]中,当i==j(行号和列号相同)时所有元素所构建成的集合称为主对角线。
如下图所示:
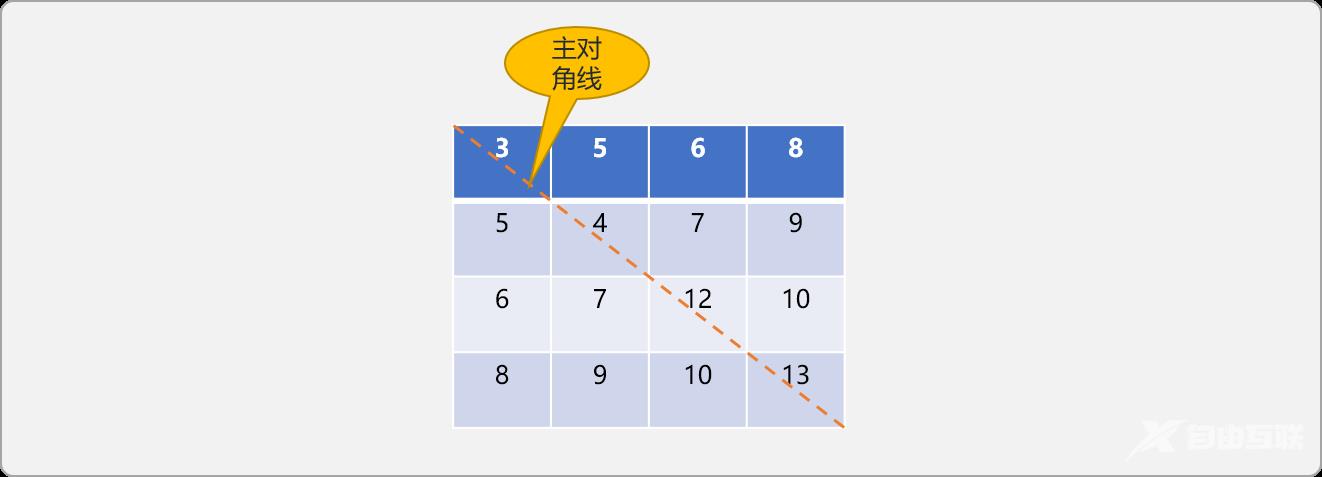
对称矩阵以主对角线为分界线,把整个矩阵分成 2 个三角区域,主对角线之上的称为上三角,主对角线之下的区域称为下三角。
对称矩阵的上三角和下三角区域中的元素是相同的,以n行n列的二维数组存储时,会浪费近一半的空间,可以采压缩机制,将 二维数组中的数据压缩存储在一个一维数组中,这个过程也称为数据线性化。
线性过程时,一维数组的空间需要多大?
n阶矩阵,使用二维数组存储,理论上所需要的存储单元应该是 n2。
对称矩阵以主对角线为分界线,上三角和下三角区域中的数据是相同的。注意,主对角线上的元素是需要单独存储的,主对角线上的数据个数为 n。
真正需要的存储单元应该:(理论上所需要的存储单元-主对角线上的数据所需单元) / 2 +主对角线上的数据所需单元。
如下表达式所述:
(n2-n)/2+n=n(n+1)/2
所以,可以把n阶矩阵中的数据可以全部压缩在长度为 n(n+1)/2 的一维数组中,能节约近一半的存储空间。并且n阶矩阵和一维数组之间满足如下的位置对应关系:
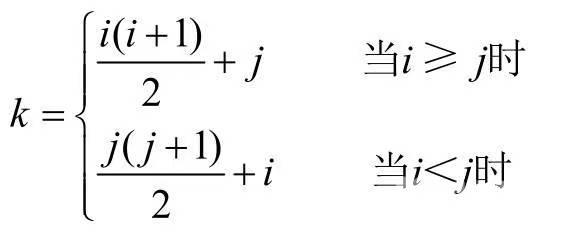
i>=j 表示矩阵中的下三角区域(包含主对角线上数据)。
i<j表示矩阵中的上三角区域。
转存实现:
#include <iostream>
using namespace std;
int main(int argc, char** argv) {
//对称矩阵
int nums[4][4]= { {3,5,6,8},{5,4,7,9},{6,7,12,10},{8,9,10,13} };
//一维数组,根据上述公式,一维数组长度为 4*(4+1)/2=10
int zipNums[10]= {0};
for(int i=0; i<4; i++) {
for(int j=0; j<4; j++) {
if (i>=j) {
zipNums[ i*(i+1)/2+j]=nums[i][j];
} else {
zipNums[ j*(j+1)/2+i]=nums[i][j];
}
}
}
for(int i=0; i<10; i++) {
cout<<zipNums[i]<<"\t";
}
return 0;
}
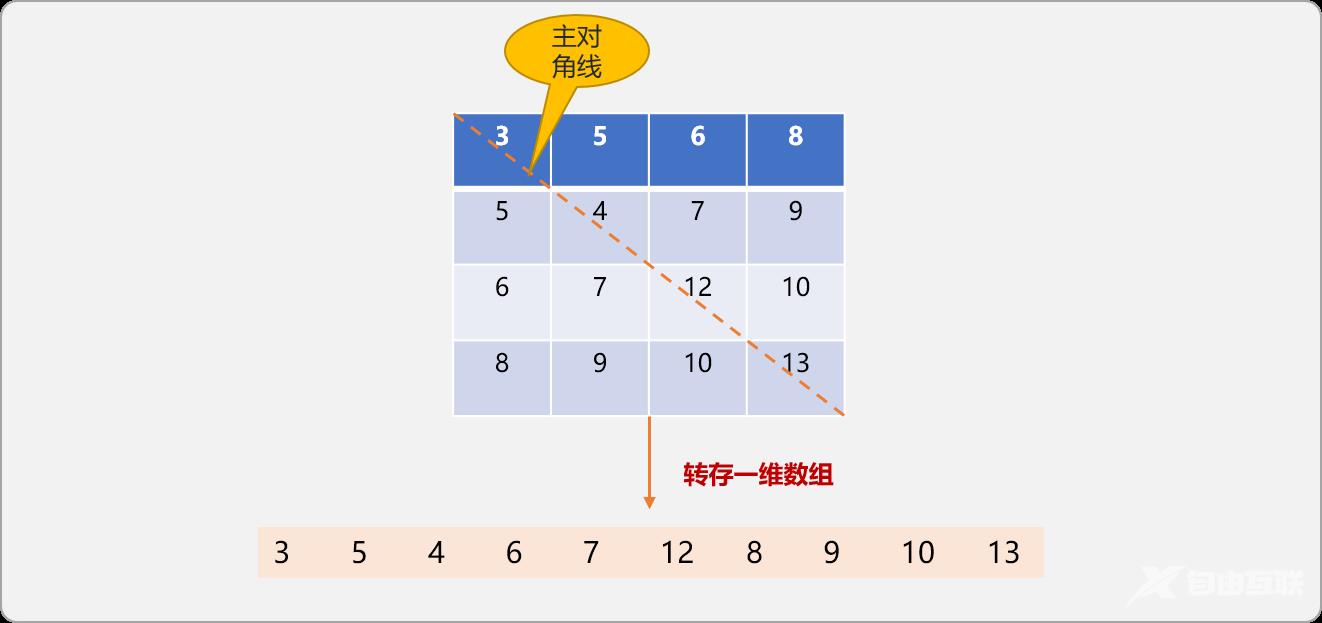
如上是二维数组压缩到一维数组后的结果。
3. 压缩稀疏矩阵
什么是稀疏矩阵?
如果矩阵A中的有效数据的数量远远小于矩阵实际能描述的数据的总数,则称A为稀疏矩阵。
现假设有 m行n列的矩阵,其中所保存的元素个数为 c,则稀疏因子为:e=c/(m*n)。当用二维数组存储稀疏矩阵中数据时,仅有少部分空间被利用,可以采用压缩机制来进行存储。
稀疏因子越小,表示有效数据越少。
稀疏矩阵中的非零数据的存储位置是没有规律的,在压缩存储时,除了需要记录非零数据本身外还需要记录其位置信息。所以需要一个三元组对象(i,j,a[i][j])对数据进行唯一性确定。
3.1 三元组表
为了便于描述,压缩前的矩阵称为原稀疏矩阵,压缩后的稀疏矩阵称三元组表矩阵。
原稀疏矩阵也好,三元组表矩阵也好。只要顶着矩阵这个概念,就应该能进行矩阵相应的操作。矩阵的内置操作有很多,本文选择矩阵的转置操作来对比压缩前和压缩后的算法差异性。
什么是矩阵转置?
如有 m行n列的A 矩阵,所谓转置,指把A变成 n行m列的 B矩阵。A和B满足 A[i][j]=B[j][i]。即A的行变成B的列。如下图所示:
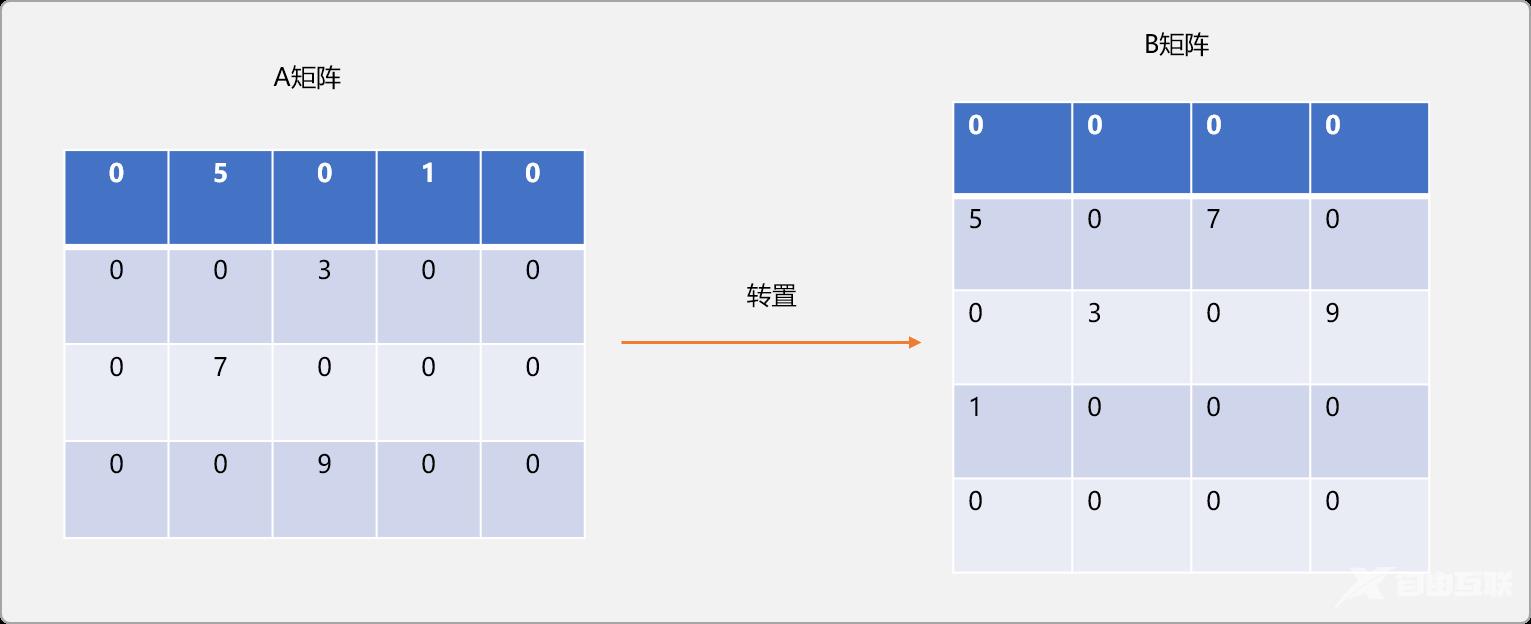
A稀疏矩阵转置成B稀疏矩阵的原生实现:
//原矩阵
int aArray[4][5]= {{0,5,0,1,0},{0,0,3,0,0},{0,7,0,0,0},{0,0,9,0,0}};
//转置后矩阵
int bArray[5][4];
//转置算法
for(int row=0; row<4; row++) {
for(int col=0; col<5; col++) {
bArray[col][row]=aArray[row][col];
}
}
基于原生矩阵上的转置算法,其时间复杂度为 O(m*n),即O(n2)。
从存储角度而言,aArray矩阵和其转置后的bArray矩阵都是稀疏矩阵,使用二维数组存储会浪费大量的空间。有必要对其以三元组表的形式进行压缩存储。
三元组表是一个一维数组,因其中的每一个存储位置需要存储原稀疏矩阵中非零数据的3 个信息(行,列,值)。三元组表名由此而来,也就是说数组中存储的是对象。
先来一个图示,直观上了解一下A稀疏矩阵压缩前后的差异性。
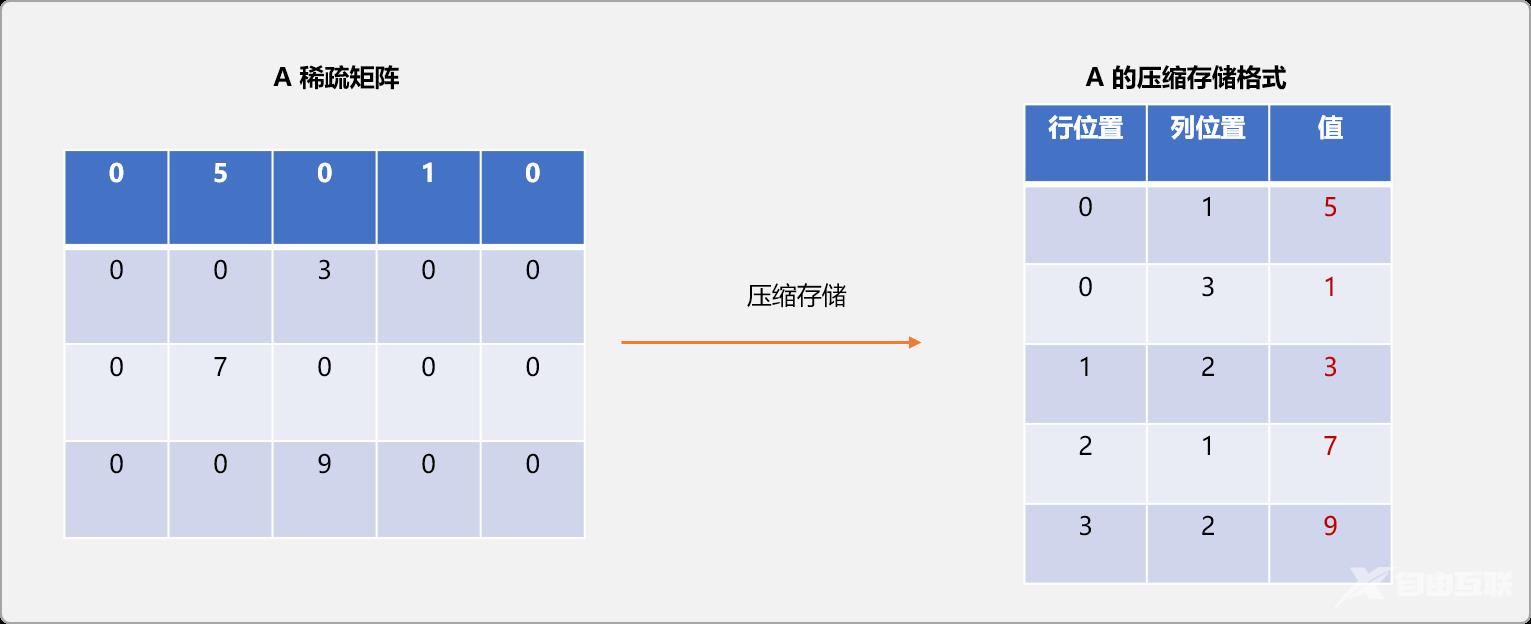
压缩算法实现:
#include <iostream>
using namespace std;
typedef int DataType;
#define maxSize 100
//三元组结构
struct Node {
//行号
int row=-1;
//列号
int col=-1;
//非零元素的值
DataType val=0;
} ;
//维护三元组表的类
class Matrix {
private:
//位置编号
int idx=0;
//压缩前稀疏矩阵的行数
int rows;
//压缩前稀疏矩阵的列数
int cols;
//原稀疏矩阵中非零数据的个数
int terms;
//压缩存储的一维数组,初始化
Node node;
Node data[maxSize]= {node};
public:
//构造函数
Matrix(int row,int col) {
this->rows=row;
this->cols=col;
this->terms=0;
}
//存储三元结点
void setData(int row ,int col,int val) {
Node n;
n.row=row;
n.col=col;
n.val=val;
this->data[idx++]=n;
//记录非零数据的数量
this->terms++;
}
//重载上面函数
void setData(int index,int row ,int col,int val) {
Node n;
n.row=row;
n.col=col;
n.val=val;
this->data[index]=n;
this->terms++;
}
//显示三无组表中的数据
void showInfo() {
for(int i=0; i<maxSize; i++ ) {
if(data[i].val==0)break;
cout<<data[i].row<<"\t"<<data[i].col<<"\t"<<data[i].val<<endl;
}
}
//基于三元组表的转置算法
Matrix transMatrix();
};
int main(int argc, char** argv) {
//原稀疏矩阵
int aArray[4][5]= {{0,5,0,1,0},{0,0,3,0,0},{0,7,0,0,0},{0,0,9,0,0}};
//实例化
Matrix matrix(4,5);
//压缩矩阵
for(int row=0; row<4; row++) {
for(int col=0; col<5; col++) {
if (aArray[row][col]!=0) {
//转存至三元组表中
matrix.setData(row,col,aArray[row][col]);
}
}
}
matrix.showInfo();
return 0;
}
代码执行后的结果和直观图示结果一致:
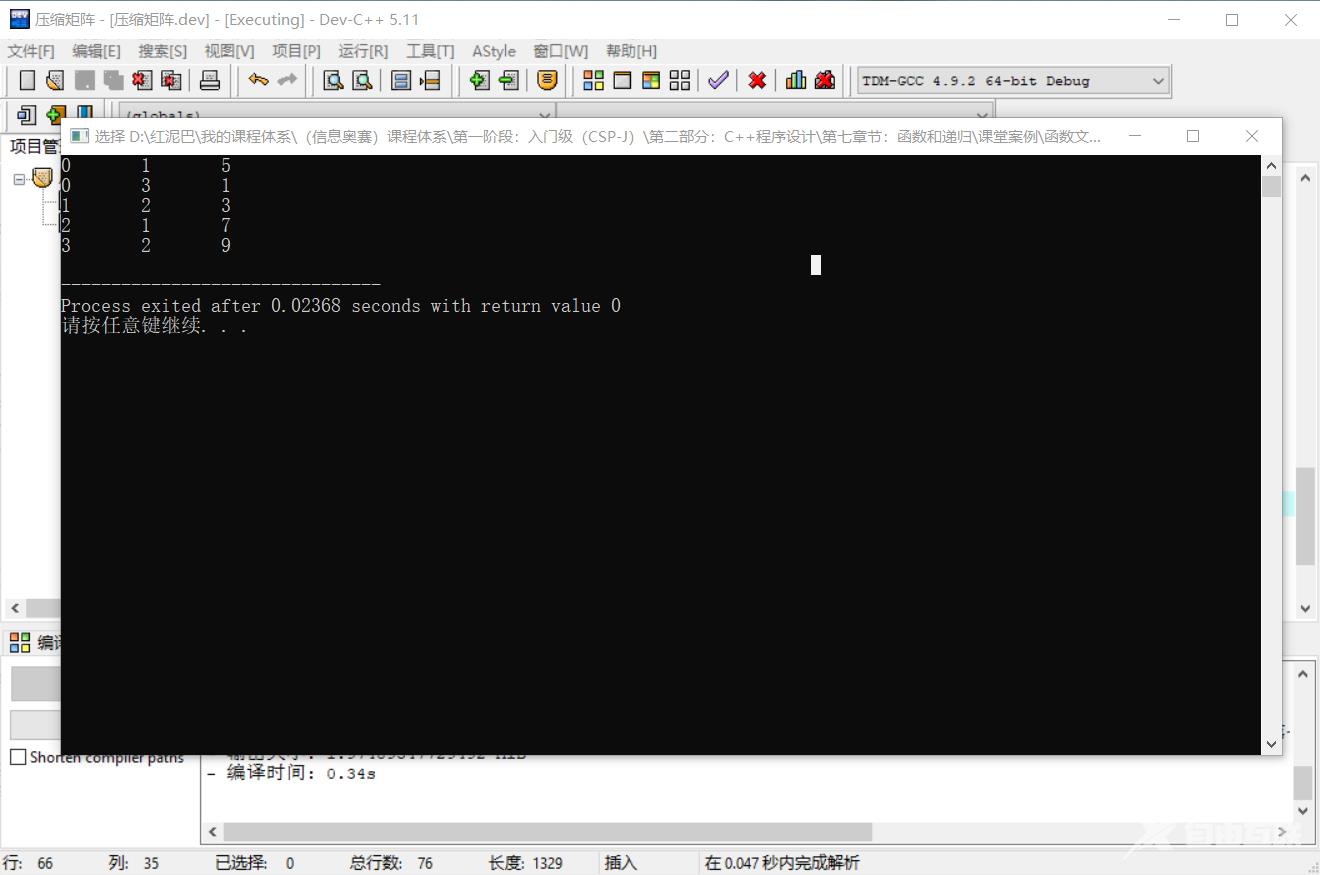
压缩之后,则要思考,如何在A三元组表的基础上直接实现矩阵的转置。或者说 ,转置后的矩阵还是使用三元组表方式描述。
先从直观上了解一下,转置后的B矩稀疏阵的三元组表的结构应该是什么样子。
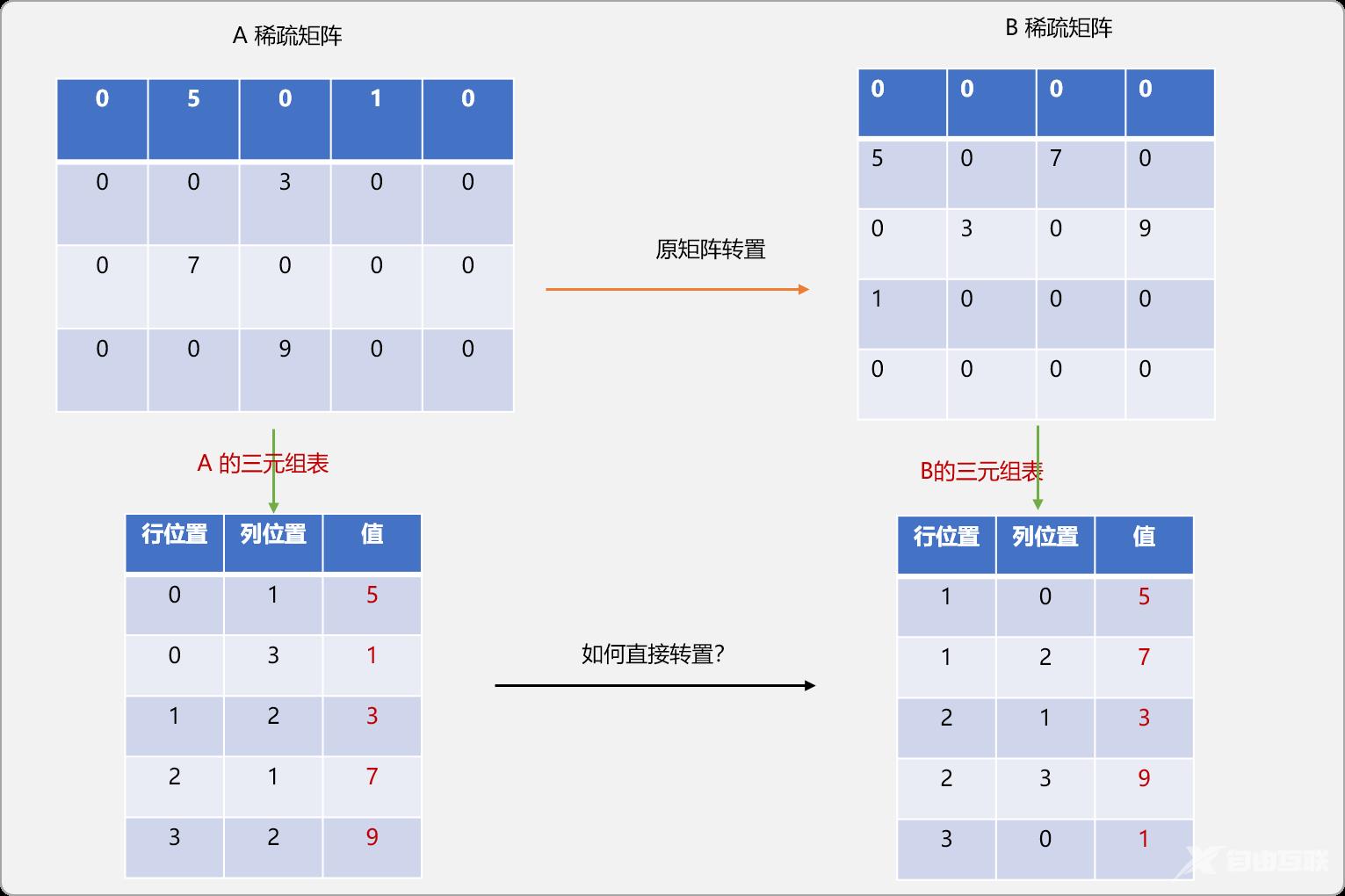
是否可以通过直接交换A的三元组表中行和列位置中的值?至于可不可以,可以先用演示图推演一下:
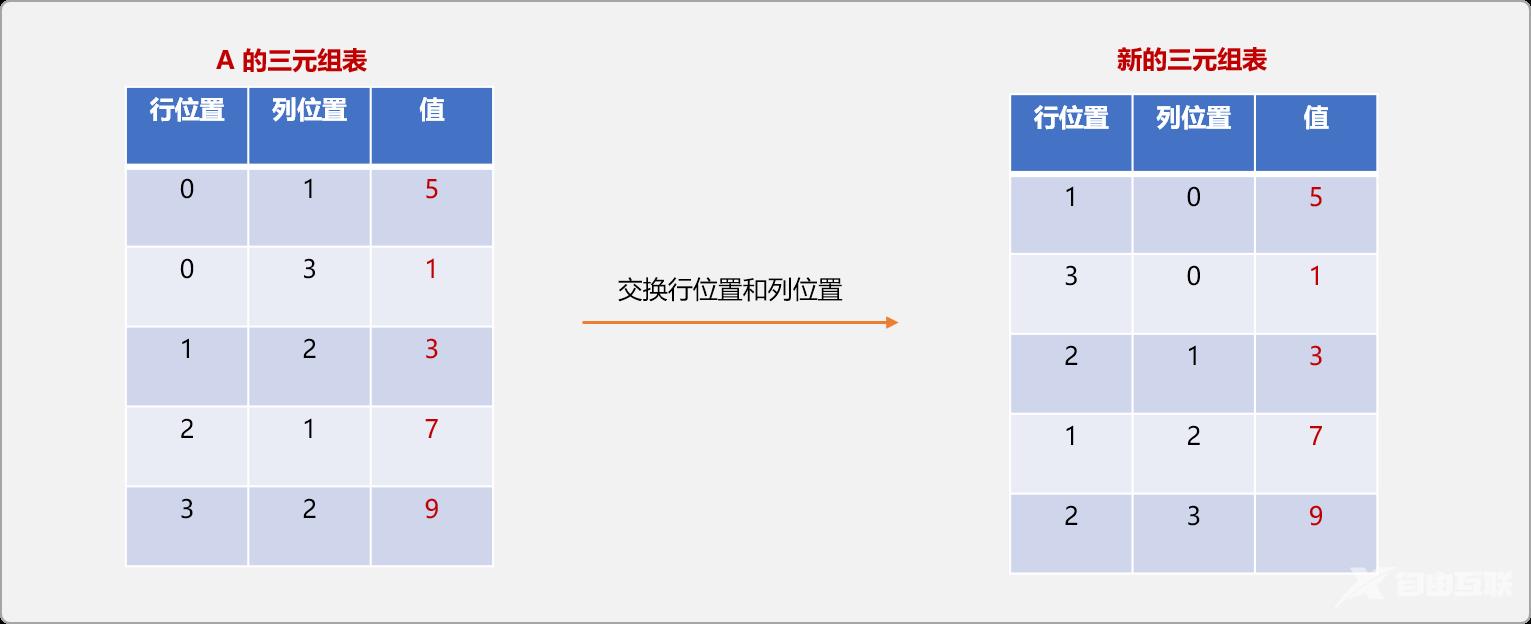
从图示可知,如果仅是交换A三元组表的行和列位置后得到的新三元组表并不和前面所推演出现的B三元组表一致。
如果仔细观察,可发现得到的新三元组表的是对原B稀疏表以列优先遍历后的结果。
B稀疏矩阵的三元组表显然应该是以行优先遍历的结果。
3.2 以列优先搜索
经过转置后,A稀疏矩阵的行会变成B稀疏矩阵的列,也可以说A的列变成B的行。如果在A中以列优先搜索,则相当于在B中以行优先进行搜索。可利用这个简单而又令人兴奋的道理实现基于三元组表的转置。
Matrix Matrix::transMatrix(){
//转置后的三元组表对象
Matrix bMatrix(this->cols,this->rows);
//对原稀疏矩阵以列优先搜索
for(int c=0;c<this->cols;c++){
//在对应的三元组表上查找此列上是否有非零数据
for(int j=0;j<this->terms;j++ ){
if(this->data[j].col==c){
//如果此列上有数据,则转置并保存
bMatrix.setData(this->data[j].col,this->data[j].row,this->data[j].val);
}
}
}
return bMatrix;
}
测试代码:
int main(int argc, char** argv) {
//原稀疏矩阵
int aArray[4][5]= {{0,5,0,1,0},{0,0,3,0,0},{0,7,0,0,0},{0,0,9,0,0}};
//实例化压缩矩阵
Matrix matrix(4,5);
//压缩矩阵
for(int row=0; row<4; row++) {
for(int col=0; col<5; col++) {
if (aArray[row][col]!=0) {
matrix.setData(row,col,aArray[row][col]);
}
}
}
cout<<"显示 A 稀疏矩阵压缩后的结果:"<<endl;
matrix.showInfo();
cout<<"在A的三元组表的基础上转置后的结果:"<<endl;
Matrix bMatrix= matrix.transMatrix();
bMatrix.showInfo();
return 0;
}
输出结果:
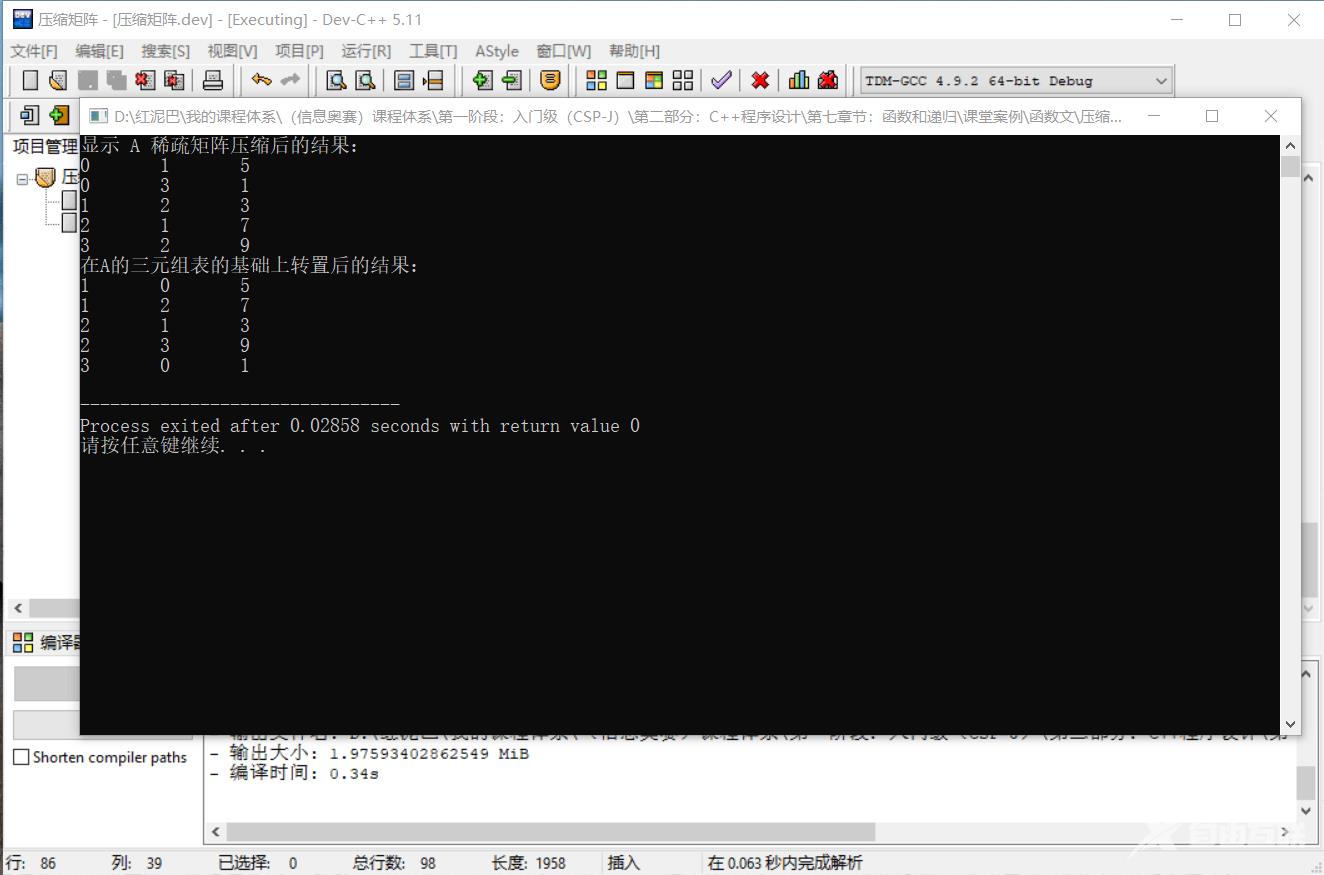
代码执行后输出的结果,和前文推演出来的结果是一样的。
前文可知,基于原生稀疏矩阵上的转置时间复杂度为 O(m*n)。基于三元组表的 时间复杂度=稀疏矩阵的列数乘以稀疏矩阵中非零数据的个数。当稀疏矩阵中的元素个数为n*m时,则上述的时间复杂度会变成 O(m*n2)。
3.3 找出存储位置
上述算法适合于当稀疏因子较小时,当矩阵中的非零数据较多时,时间复杂度会较高。可以在上述列优先搜索的算法基础上进行优化。
其核心思路如下所述:
- 在原A稀疏矩阵中按列优先进行搜索。
- 统计每一列中非零数据的个数。
- 记录每一列中第一个非零数据在
B三元组表中的位置。
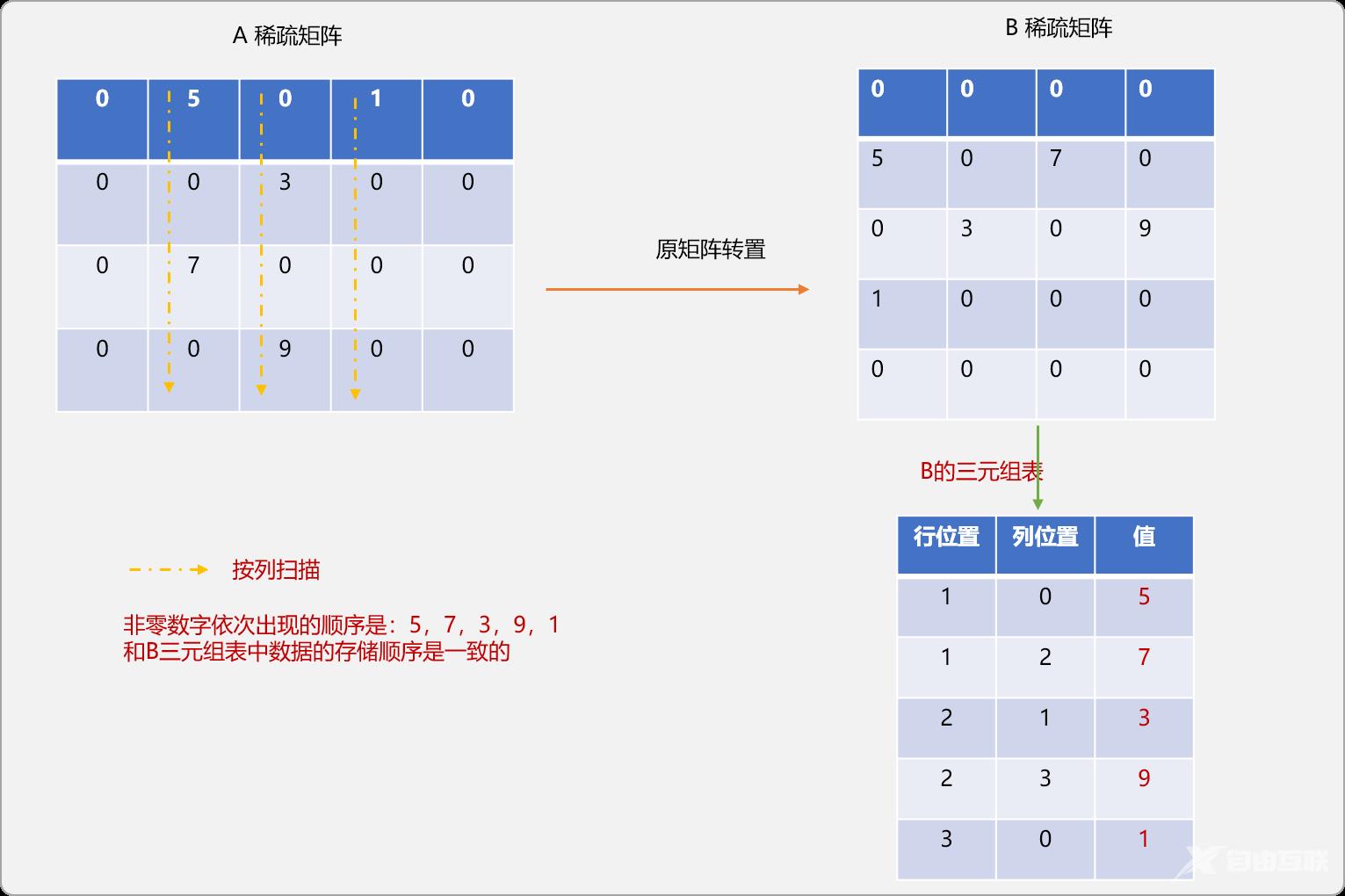
对A稀疏矩阵按列遍历时,可以发现,扫描时,数据出现的顺序和其在B三元组表中的存储顺序是一致的。
如果在遍历时,能记录每列非零数据在B三元组表中应该存储的位置,则可以实现A三元组表中的数据直接以转置要求存储在B三元组表中。

重写上述的转置函数。
Matrix Matrix::transMatrix() {
//保存转置后数据的压缩矩阵
Matrix bMatrix(this->cols,this->rows);
//初始化数组,用来保存A稀疏矩阵中第一列中非零数据的个数
int counts[this->cols]= {0};
//计算每一列中非零数据个数
for(int i=0; i<this->terms; i++)
counts[this->data[i].col]++;
//初始化数组,用来保存A稀疏矩阵每列中非零数据在B三元组表中的起始位置
int position[this->cols]= {0};
for(int i=1;i<this->cols;i++ ){
//上一列的起始位置加上上一列非零数据的个数
position[i]=position[i-1]+counts[i-1];
}
//转置A三元组表
for(int i=0;i<this->terms;i++){
int col=this->data[i].col;
int row=this->data[i].row;
int val=this->data[i].val;
//找到在B三元组中的起始存储位置
int pos=position[col];
bMatrix.setData(pos,col,row,val);
position[col]++;
}
return bMatrix;
}
测试代码不需要任何变化:
int main(int argc, char** argv) {
//原稀疏矩阵
int aArray[4][5]= {{0,5,0,1,0},{0,0,3,0,0},{0,7,0,0,0},{0,0,9,0,0}};
//实例化压缩矩阵
Matrix matrix(4,5);
//压缩矩阵
for(int row=0; row<4; row++) {
for(int col=0; col<5; col++) {
if (aArray[row][col]!=0) {
matrix.setData(row,col,aArray[row][col]);
}
}
}
cout<<"显示 A 稀疏矩阵压缩后的结果:"<<endl;
matrix.showInfo();
cout<<"在A的三元组表的基础上转置后的结果:"<<endl;
Matrix bMatrix= matrix.transMatrix();
bMatrix.showInfo();
return 0;
}
输出结果:
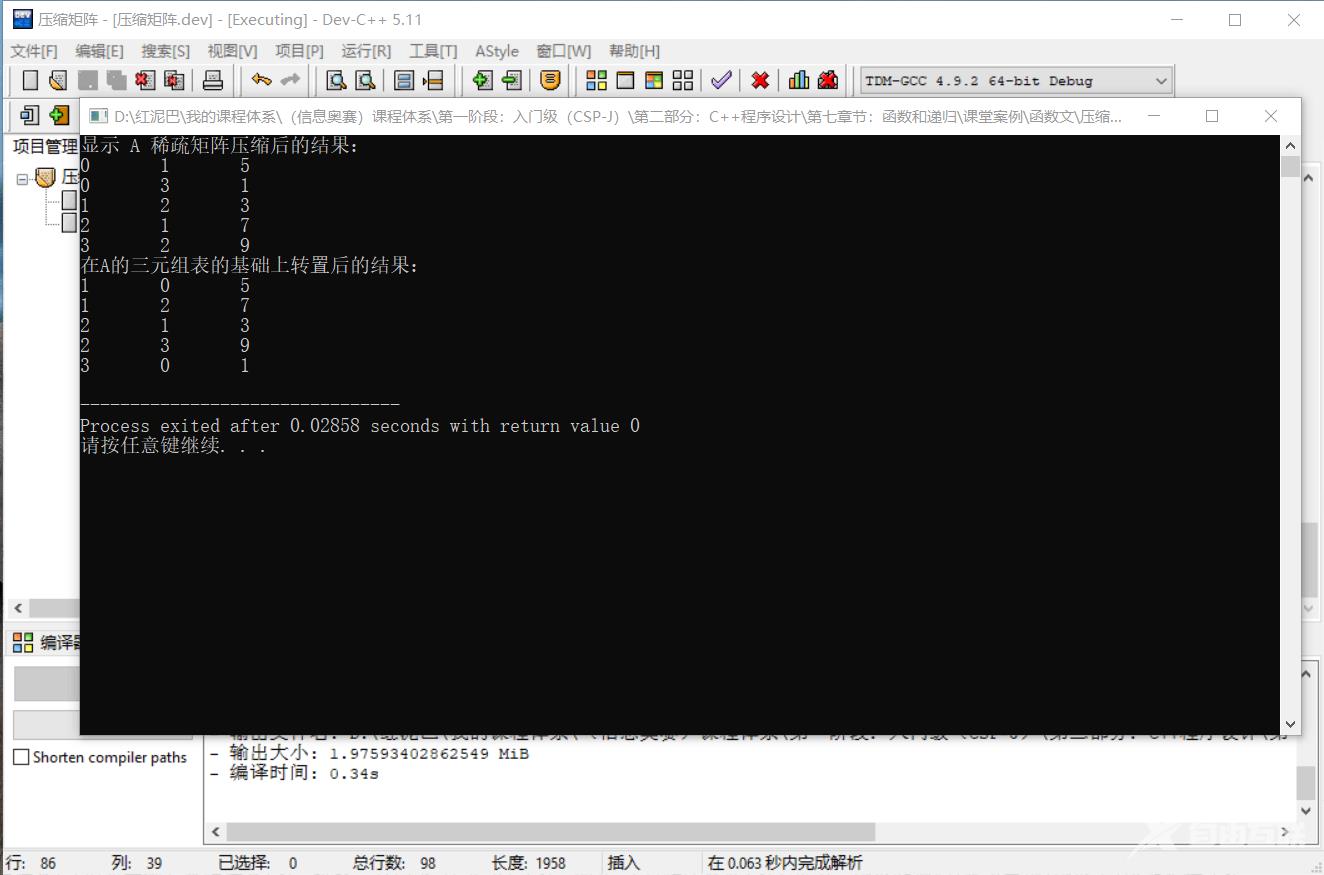
上述 2 种转置算法,其本质是一样的,第一种方案更容易理解,第二种方案在第一种方案的基础上用空间换取了时间上性能的提升。
4. 总结
使用二维数组存储矩阵中数据时,如果矩阵中的有效数据较小时,可以采用压缩的方式对其进行存储。
本文着重讲解如何使用三元组表方式压缩存储稀疏矩阵。转存过程并不难,难点在于转存为三元组表后,如何在三元组表的基础上正常进行矩阵相关操作。
以上就是C++实现特殊矩阵的压缩存储算法的详细内容,更多关于C++矩阵压缩存储的资料请关注自由互联其它相关文章!
