一、线索二叉树概述
线索二叉树是一种特殊的二叉树,它通过添加线索(thread)来将一棵普通的二叉树转化为可以快速遍历的二叉树。线索化就是将一个结点的指针空闲时利用起来,指向该节点的前驱或后继,这样就可以在不使用递归的情况下实现对树的遍历。由于线索化的过程可以提前完成,因此线索二叉树具有很好的时间和空间优势。
二、线索二叉树的节点结构
线索二叉树的节点结构如下:
typedef struct TreeNode
{
int val; // 节点的值
TreeNode* left; // 左子节点指针
TreeNode* right; // 右子节点指针
int lTag; // 左标志位:0 表示左指针,1 表示前驱
int rTag; // 右标志位:0 表示右指针,1 表示后继
} TreeNode;
其中,节点包含以下几个成员变量:
- val:节点存储的数据值;
- left:指向节点左子树的指针;
- right:指向节点右子树的指针;
- lTag:左标志位,用于表示节点的左指针状态。当 lTag = 0 时,表示 left 指向左子节点;当 lTag = 1 时,表示 left 指向该节点的前驱节点;
- rTag:右标志位,用于表示节点的右指针状态。当 rTag = 0 时,表示 right 指向右子节点;当 rTag = 1 时,表示 right 指向该节点的后继节点。
通过线索化的方式,可以将原有的二叉树的指针空闲时利用起来,把一些原先为空的指针指向该节点的前驱或后继节点。这样,在遍历时就可以快速地找到节点的前驱和后继节点,从而实现非递归遍历二叉树的目的。而 lTag 和 rTag 就是用来记录这些指针的状态,并指示其指向的位置的标志位。
三、线索二叉树的初始化
(1)节点初始化
先把左右指针还有标志域lTag和rTag都进行初始化,修改数值域val进行赋值。
TreeNode* CreateNode(int val)
{
TreeNode* node = new TreeNode();
node->val = val;
node->left = nullptr;
node->right = nullptr;
node->lTag = 0;
node->rTag = 0;
return node;
}(2)创建一颗线索二叉树
这里采用手动建树的方法实现创建一颗线索二叉树
TreeNode* CreateThreadedTree()
{
TreeNode* root = CreateNode(1);
root->left = CreateNode(2);
root->right = CreateNode(3);
root->left->left = CreateNode(4);
root->left->right = CreateNode(5);
root->right->left = CreateNode(6);
root->right->right = CreateNode(7);
return root;
}四、线索二叉树的遍历方法
线索二叉树的遍历方法可以分为两种:中序遍历和前序遍历。其中,中序遍历是最常用的。
(1) 中序遍历
在线索二叉树中,中序遍历方式与普通的中序遍历方式略有不同。对于任意一个结点,先访问其左子树,在访问该节点时,如果它的左指针为空,则将其左指针指向它的前驱结点,如果它的右指针为空,则将其右指针指向它的后继节点。然后再访问其右子树。
中序遍历的顺序为:左子树 => 根节点 => 右子树。
(2) 前序遍历
前序遍历方式与中序遍历方式类似。对于任意一个结点,先访问该节点,在访问其左子树和右子树时,如果它的左指针为空,则将其左指针指向它的前驱结点,如果它的右指针为空,则将其右指针指向它的后继节点。
前序遍历的顺序为:根节点 => 左子树 => 右子树。
五、线索化的实现方法
(1)递归实现:
线索化的实现可以分为两种方式:一种是递归实现,另一种是非递归实现。递归实现比较简单,我们以中序线索化为例进行说明:
void InOrderThread(TreeNode* root, TreeNode*& prev)
{
if (root == nullptr)
{
return;
}
// 线索化左子树
InOrderThread(root->left, prev);
// 左指针处理
if (root->left == nullptr)
{
root->left = prev;
root->lTag = THREAD;
}
// 右指针处理
if (prev != nullptr && prev->right == nullptr)
{
prev->right = root;
prev->rTag = THREAD;
}
// 更新前驱指针
prev = root;
// 线索化右子树
InOrderThread(root->right, prev);
}实现如下图结构:
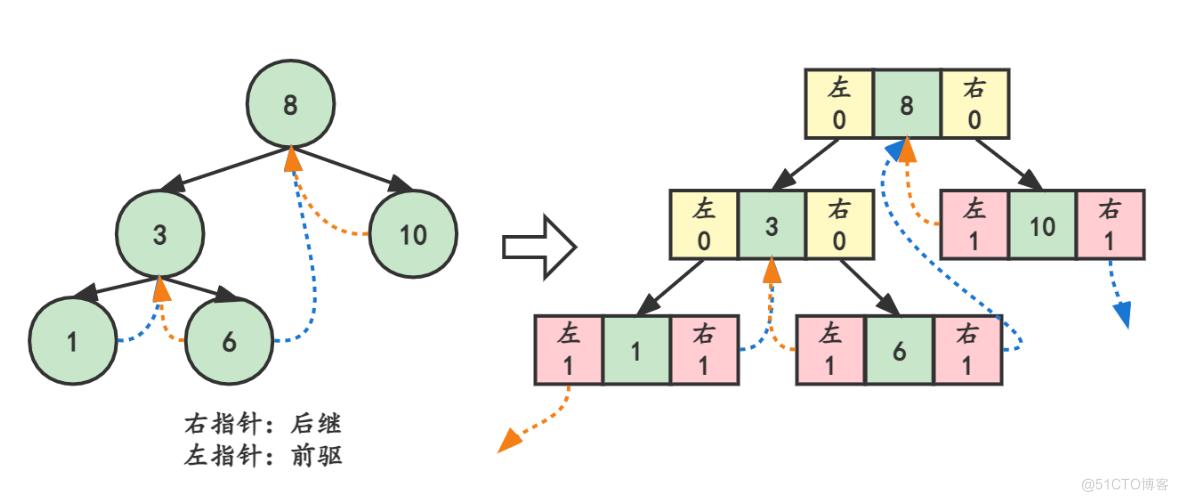
(2)非递归实现:
对于非递归实现方式,我们需要使用栈来模拟递归的调用过程。具体的实现可以参考以下代码:
// 中序遍历线索化(非递归)
void InOrderThread(TreeNode* root)
{
if (root == nullptr)
{
return;
}
stack<TreeNode*> s;
TreeNode* cur = root;
TreeNode* prev = nullptr;
while (!s.empty() || cur != nullptr)
{
while (cur != nullptr)
{
s.push(cur);
cur = cur->left;
}
cur = s.top();
s.pop();
// 左指针处理
if (cur->left == nullptr)
{
cur->left = prev;
cur->lTag = THREAD;
}
// 右指针处理
if (prev != nullptr && prev->right == nullptr)
{
prev->right = cur;
prev->rTag = THREAD;
}
// 更新前驱指针
prev = cur;
cur = cur->right;
}
}六、线索二叉树的销毁
一定要注意写一个销毁的函数,防止内存泄漏
// 销毁线索化二叉树
void DestroyThreadedTree(TreeNode*& root)
{
if (root == nullptr)
{
return;
}
DestroyThreadedTree(root->left);
DestroyThreadedTree(root->right);
delete root;
root = nullptr;
}七、线索二叉树的实际应用
线索二叉树可以应用于二叉树的遍历、查找和删除等操作。由于线索二叉树在遍历时可以不使用递归,因此可以大大减少程序运行时的空间开销。线索二叉树还可以用于构建哈夫曼树和表达式树,以及解析JSON数据等场景。
八、线索二叉树完整实现代码
#include <iostream>
#include <stack>
using namespace std;
// 标志位常量定义
const int POINTER = 0; // 指针标志
const int THREAD = 1; // 线索标志
// 节点结构体定义
typedef struct TreeNode
{
int val; // 节点的值
TreeNode* left; // 左子节点指针
TreeNode* right; // 右子节点指针
int lTag; // 左标志位:0 表示左指针,1 表示前驱
int rTag; // 右标志位:0 表示右指针,1 表示后继
} TreeNode;
/**
* 创建一个节点
* @param val 节点的值
* @return 新创建的节点
*/
TreeNode* CreateNode(int val)
{
TreeNode* node = new TreeNode();
node->val = val;
node->left = nullptr;
node->right = nullptr;
node->lTag = 0;
node->rTag = 0;
return node;
}
/**
* 创建一颗线索化二叉树
* @return 根节点
*/
TreeNode* CreateThreadedTree()
{
TreeNode* root = CreateNode(1);
root->left = CreateNode(2);
root->right = CreateNode(3);
root->left->left = CreateNode(4);
root->left->right = CreateNode(5);
root->right->left = CreateNode(6);
root->right->right = CreateNode(7);
return root;
}
/**
* 销毁线索化二叉树
* @param root 指向根节点的指针的引用
*/
void DestroyThreadedTree(TreeNode*& root)
{
if (root == nullptr)
{
return;
}
DestroyThreadedTree(root->left);
DestroyThreadedTree(root->right);
delete root;
root = nullptr;
}
/**
* 中序遍历(非递归)
* @param root 根节点
*/
void InOrderTraversal(TreeNode* root)
{
if (root == nullptr)
{
return;
}
stack<TreeNode*> s;
TreeNode* cur = root;
while (!s.empty() || cur != nullptr)
{
while (cur != nullptr)
{
s.push(cur);
cur = cur->left;
}
cur = s.top();
s.pop();
cout << cur->val << " ";
cur = cur->right;
}
}
/**
* 中序遍历(线索化方式)
* @param root 根节点
*/
void InOrderThreadTraversal(TreeNode* root)
{
if (root == nullptr)
{
return;
}
// 找到第一个结点
while (root->left != nullptr)
{
root = root->left;
}
while (root != nullptr)
{
cout << root->val << " ";
if (root->rTag == THREAD)
{
root = root->right;
}
else
{
root = root->right;
// 找到下一个要访问的结点
while (root != nullptr && root->lTag == 0)
{
root = root->left;
}
}
}
}
/**
* 中序遍历线索化二叉树,并修改结点的标志位
* @param root 根节点
* @param pre 前驱节点的引用
*/
void InOrderThread(TreeNode* root, TreeNode*& pre)
{
if (root == nullptr)
{
return;
}
InOrderThread(root->left, pre);
// 处理当前节点
if (root->left == nullptr)
{
root->left = pre;
root->lTag = THREAD;
}
if (pre != nullptr && pre->right == nullptr)
{
pre->right = root;
pre->rTag = THREAD;
}
pre = root;
InOrderThread(root->right, pre);
}
/**
* 对二叉树进行中序遍历线索化
* @param root 根节点
*/
void InOrderThreading(TreeNode* root)
{
TreeNode* pre = nullptr;
if (root != nullptr)
{
InOrderThread(root, pre);
pre->right = nullptr;
pre->rTag = THREAD;
}
}
int main()
{
// 创建线索化二叉树
TreeNode* root = CreateThreadedTree();
// 对二叉树进行中序遍历线索化
InOrderThreading(root);
// 中序遍历线索化二叉树(非递归方式)
cout << "中序遍历(线索化方式):";
InOrderThreadTraversal(root);
cout << endl;
// 销毁线索化二叉树
DestroyThreadedTree(root);
return 0;
}