LLE降维算法

流形分析作为非线性降维的一个分支，拥有多种算法，常见的算法列表如下

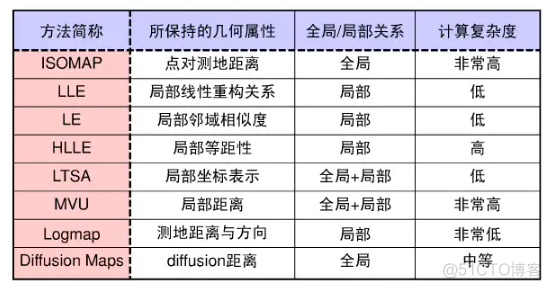
流形分析的要点在于降维之后，仍然保留流形中的某些几何属性。之前介绍的isomap保留了测地距离这一几何属性，由于考虑的是全局关系，对于样本量大，维度非常高的数据，计算量很大。本片文章的主角LLE算法，保留的是局部样本点之间的线性关系，算法复杂度低，运行速度更快。LLE全称如下

Locally Linear Embedding

称之为局部线性嵌入算法，在该算法中，假设邻近样本符合线性关系，对于样本x1而言，可以看做是邻近样本x2, x3, x4的线性组合

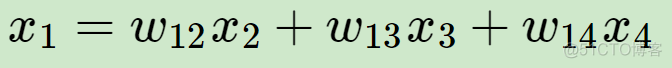
降维之后，也希望保留这种线性关系，即权重系数不变，新的坐标依然保持线性关系，公式如下

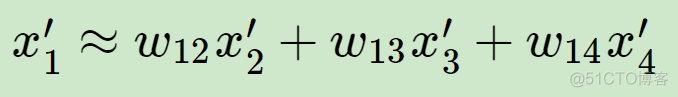
基于这一思想，该算法可以分为以下3步

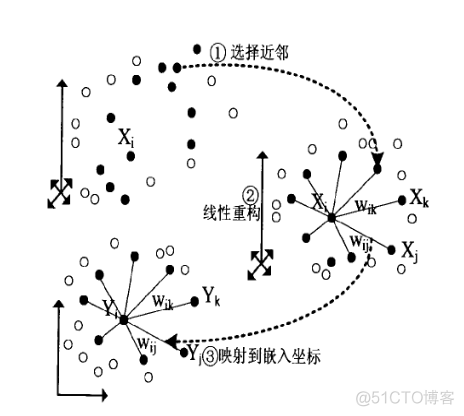
1. 选择样本的邻近点。这里选择的方法和KNN类似，按照欧式距离排序，选择前K个邻近点

2. 对于每个样本，拟合其邻近样本的线性关系，计算样本点的局部重建权值矩阵

3. 根据邻近点与局部重建权值矩阵，计算降维后的输出值

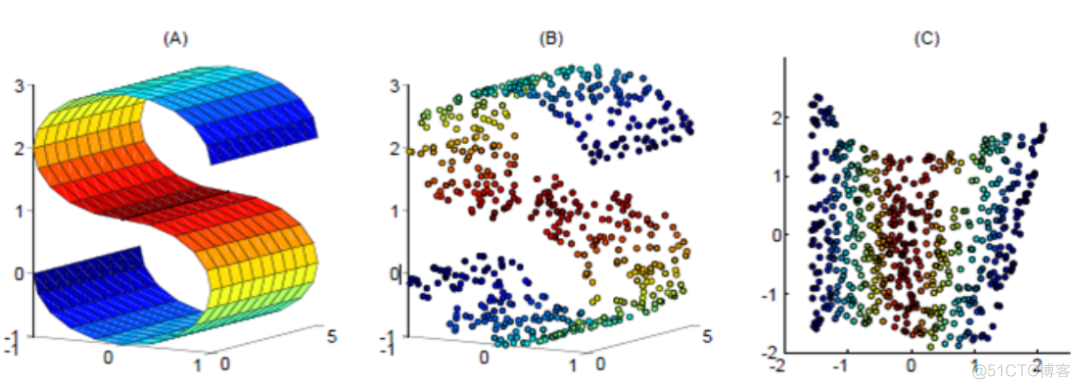
LLE算法降维的结果示例如下

在sickit-learn中使用LLE算法的代码如下

>>> from sklearn.datasets import make_swiss_roll
>>> from sklearn.manifold import locally_linear_embedding
>>> x, color = make_swiss_roll(n_samples=1500)
>>> x_r, err = locally_linear_embedding(x, n_neighbors=12, n_components=2)
>>> x_r
array([[ 0.04141383, -0.01174298],
[ 0.00866775, 0.01427625],
[-0.00896186, 0.00451398],
...,
[ 0.00950672, 0.01665103],
[ 0.04236568, -0.01045307],
[-0.02801082, 0.00123999]])

LLE算法实现简单，对数据维度没有任何限制，但是对数据的流形分布有严格要求，要求不能是闭合流形，同时该算法对近邻样本数目K的选择也较为敏感。

·end·

一个只分享干货的

生信公众号

【文章原创作者：韩国高防服务器 http://www.558idc.com/krgf.html 网络转载请说明出处】