数据结构——最大堆

一、堆

堆（英语：heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一棵完全二叉树。

堆的实现通过构造二叉堆（binary heap），实为二叉树的一种；由于其应用的普遍性，当不加限定时，均指该数据结构的这种实现。这种数据结构具有以下性质。

• 任意节点小于（或大于）它的所有后裔，最小元（或最大元）在堆的根上（堆序性）。
• 堆总是一棵完全树。即除了最底层，其他层的节点都被元素填满，且最底层尽可能地从左到右填入。

将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

 

我们这里讲的是二叉堆。

堆的入队和出队的时间复杂度都是O(log n)

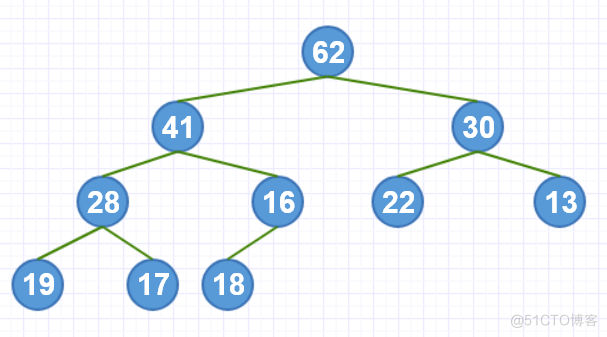
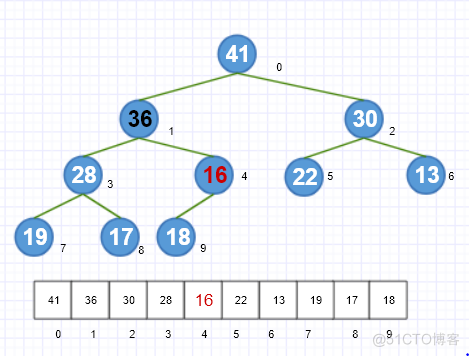
上图就是一个最大堆的事例

下面我们使用数组来构建一个最大堆，在这里为了便于理解，数组索引为0的节点不存放数值，从第二个节点开始存放数据。

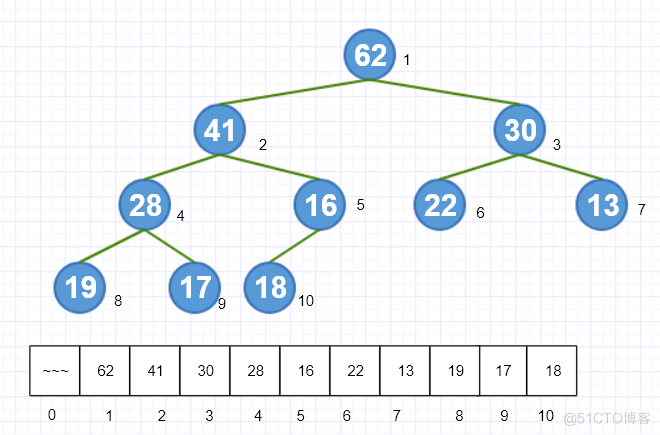
当前节点的父节点、左孩子、右孩子的索引就会有如下的关系：

• 父节点的索引：index/2 (index为当前节点的索引)
• 左孩子的索引：index*2
• 右孩子的索引：index*2+1

如果从数组的第一个节点开始存放数据的话，当前节点的父节点、左孩子、右孩子的索引就会有如下的关系：

• 父节点的索引：(index-1)/2 (index为当前节点的索引)
• 左孩子的索引：index*2+1
• 右孩子的索引：index*2+2

二、优先队列

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 （first in, largest out）的行为特征。通常采用堆数据结构来实现。

三、最大堆的基础架构

3.1 动态数组的底层实现

public class Array<E> { private E[] data; private int size; public Array(){ this(10); } public Array(int capacity){ this.data = (E[]) new Object[capacity]; this.size = 0; } public Array(E[] arr){ this.data = (E[]) new Object[arr.length]; for (int i = 0; i < arr.length; i++) { data[i] = arr[i]; } this.size = arr.length; } /** * 获取数组中元素个数 * @return */ public int getSize(){ return size; } /** * 获取数组容量 * @return */ public int getCapacity(){ return data.length; } /** * 返回数组是否为空 * @return */ public boolean isEmpty(){ return size == 0; } /** * 数组尾部新增元素 * @param e */ public void addLast(E e){ add(size, e); } /** * 数组头部新增元素 * @param e */ public void addFirst(E e){ add(0, e); } /** * 在指定位置插入元素 * @param index * @param e */ public void add(int index, E e){ if(index < 0 || index > size){ throw new IllegalArgumentException("AddLast failed. require index >=0 and index <= size"); } if(size == data.length){ //扩容 resize(2 * data.length); } for(int i = size - 1; i >= index; i --){ data[i + 1] = data[i]; } data[index] = e; size ++; } /** * 数组扩容 * @param newCapacity */ private void resize(int newCapacity){ E[] newData = (E[])new Object[newCapacity]; for (int i = 0; i < size; i++) { newData[i] = data[i]; } data = newData; } /** * 获取指定索引位置的值 * @param index * @return */ public E get(int index){ if(index < 0 || index >= size){ throw new IllegalArgumentException("Get failed. index is illegal."); } return data[index]; } /** * 替换指定索引位置的值 * @param index * @param e */ public void set(int index, E e){ if(index < 0 || index >= size){ throw new IllegalArgumentException("Set failed. index is illegal."); } data[index] = e; } /** * 数组是否包含元素e * @param e * @return */ public boolean contains(E e){ for (int i = 0; i < size; i++) { if(data[i].equals(e)){ return true; } } return false; } /** * 查找数组中元素e所在的索引,不存在元素e,返回-1 * @param e * @return */ public int find(E e){ for (int i = 0; i < size; i++) { if(data[i].equals(e)){ return i; } } return -1; } /** * 删除数组中index位置的元素, 并返回删除的元素 * @param index * @return */ public E remove(int index){ if(index < 0 || index >= size){ throw new IllegalArgumentException("Remove failed. index is illegal."); } E ret = data[index]; for (int i = index; i < size - 1; i++) { data[i] = data[i + 1]; } size --; data[size] = null; if(size == data.length / 4 && data.length / 2 != 0){ //当数组长度缩小为原数组的4分之一的时候才进行数组的缩容， //缩小为原数组的2分之一，预留空间，防止有数据添加导致扩容浪费性能 resize(data.length / 2); } return ret; } /** * 删除数组中第一个元素 * @return */ public E removeFirst(){ return remove(0); } /** * 删除数组中最后一个元素 * @return */ public E removeLast(){ return remove(size - 1); } /** * 从数组中删除元素e * @param e */ public void removeElement(E e){ int index = find(e); if(index != -1){ remove(index); } } /** * 数组索引元素交换 * @param i * @param j */ public void swap(int i, int j){ if(i < 0 || i >= size || j < 0 || j >= size){ throw new IllegalArgumentException("Index is illegal."); } E temp = data[i]; data[i] = data[j]; data[j] = temp; } @Override public String toString(){ StringBuilder sb = new StringBuilder(); sb.append(String.format("Array: size = %d, capacity = %d\n",size,data.length)); sb.append("["); for (int i = 0; i < size; i++) { sb.append(data[i]); if(i != size - 1){ sb.append(", "); } } sb.append("]"); return sb.toString(); } }

3.2 最大堆使用动态数组作为底层实现

/** * @Author: huangyibo * @Date: 2022/2/17 22:54 * @Description: 最大堆 完全二叉树，父亲节点大于等于孩子节点，采用数组表示 */ public class MaxHeap<E extends Comparable<E>> { //这里使用数组来实现 private Array<E> data; public MaxHeap(){ data = new Array<>(); } public MaxHeap(int capacity){ data = new Array<>(capacity); } /** * 返回堆中的元素个数 * @return */ public int getSize(){ return data.getSize(); } /** *堆是否为空 * @return */ public boolean isEmpty(){ return data.isEmpty(); } /** * 返回完全二叉树的数组表示中，一个索引所表示的元素的父亲节点的索引 * @param index * @return */ private int parent(int index){ if(index == 0){ throw new IllegalArgumentException("index-0 doesn't have parent."); } return (index - 1) / 2; } /** * 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引 * @return */ private int leftChild(int index){ return index * 2 + 1; } /** * 回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引 * @param index * @return */ private int rightChild(int index){ return index * 2 + 2; } }

3.3 往堆中添加元素

• 在向堆中添加元素时，除了要维持完全二叉树的结构，还要注意堆的约束条件：根节点的值要大于左右子树的值。

在这里因为我们使用数组来实现的堆，所以添加元素时，我们可以先将元素添加到数组的末尾，然后循环的与父节点比较大小，比父节点大就与父节点交换位置，之后就继续与新的父节点比较大小，直到小于等于父节点。

• 如图所示，我们要在这个堆中添加一个元素36。

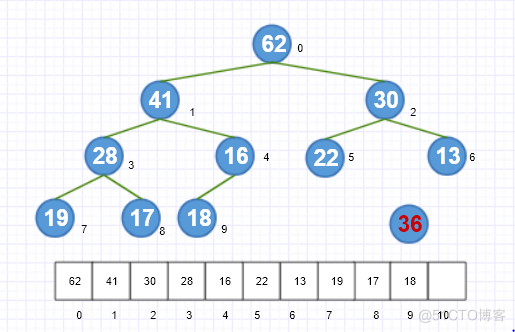
• 先将元素添加到数组的末尾。

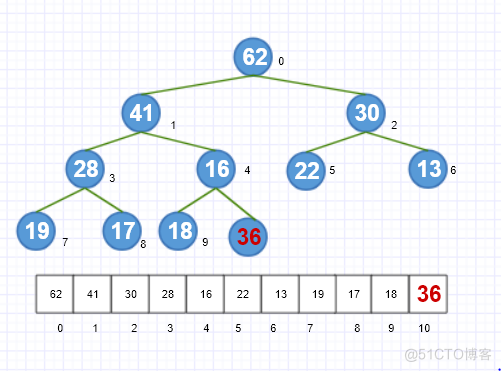
• 然后通过当前的索引计算出父节点的索引，通过索引得到父节点的值16，通过比较新添加的节点比其父节点大，所以将新添加的值与父节点交换在数组中的位置。之后再与新的父节点41比较，36<41，结束操作。

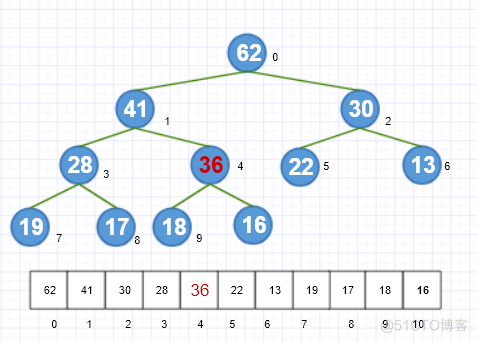
添加元素的代码实现

/** * 向堆中添加元素 * @param e */ public void add(E e){ data.addLast(e); //当前元素在数组中的索引为 data.getSize() - 1 //比较当前元素和其父亲节点的元素，大于父亲节点元素则交换位置 siftUp(data.getSize() - 1); } /** * k索引元素比父节点元素大，则交换位置，不断循环 * @param k */ private void siftUp(int k){ //k > 0 并且k索引元素比父节点元素大，则交换位置，不断循环 while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0){ data.swap(parent(k), k); k = parent(k); } }

3.4 删除堆顶元素

删除堆顶元素要注意维持堆的特殊性质。这里举个例子。

• 要将这个堆中删除最大值，也就是堆顶元素62，先将62取出。

• 将堆顶元素和堆的最后一个元素互换，也就是数组的首尾元素互换。

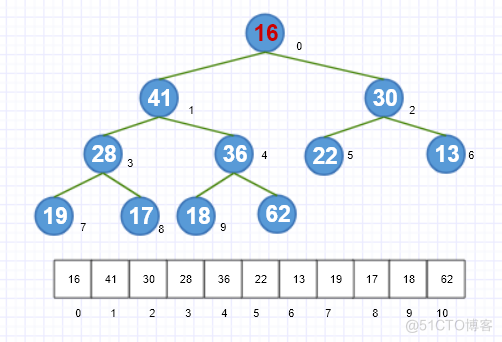
• 删除最后一个元素，也就是堆中的最大值

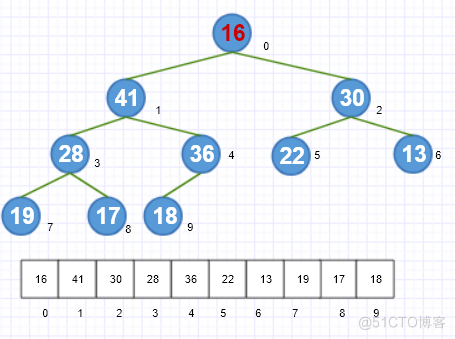
• 将当前的堆顶元素16的左右孩子41、30进行比较，找出最大的一个41，再与根节点16进行比较，左孩子41比根节点16大，所以将根节点与其左孩子互换，如图所示。

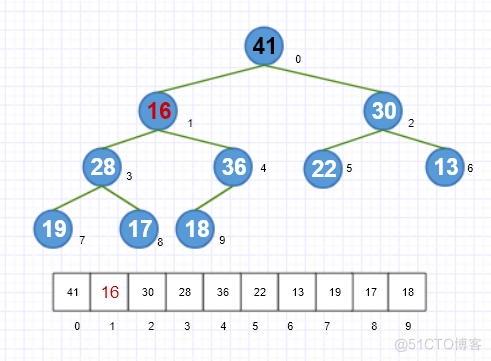
• 重复上面的操作，直到当前节点的值大于其左右子树。过程如下所示。

删除堆顶元素的代码实现

/** * 查看堆中最大元素 * @return */ public E findMax(){ if(data.getSize() == 0){ throw new IllegalArgumentException("Can not findMax when heap is empty."); } return data.get(0); } /** * 取出堆中最大元素 * @return */ public E extractMax(){ //获取堆中最大元素 E ret = findMax(); //堆中最开始的元素和最后元素交换位置 data.swap(0,data.getSize() - 1); //删除堆中最后一个元素 data.removeLast(); //0索引元素比左右孩子节点元素小，则交换位置，不断循环 siftDown(0); return ret; } /** * k索引元素比左右孩子节点元素小，则交换位置，不断循环 * @param k */ private void siftDown(int k){ while (leftChild(k) < data.getSize()){ //获取k索引的左孩子的索引 int j = leftChild(k); //j + 1 < data.getSize() if(j + 1 < data.getSize() && //如果右孩子比左孩子大 data.get(j + 1).compareTo(data.get(j)) > 0){ //最大孩子的索引赋值给j j = rightChild(k); } //此时data[j]是leftChild和rightChild中的最大值 if(data.get(k).compareTo(data.get(j)) >= 0){ //如果父亲节点大于等于左右孩子节点，跳出循环 break; } //如果父亲节点小于左右孩子节点(中的最大值)，交换索引的值 data.swap(k, j); //交换完成之后，将j赋值给K,重新进入循环 k = j; } }

3.5 Replace操作

Replace是指将堆中的最大元素取出，替换另一个进去。

 

自然地我们会想到使用之前的extractMax()和add()来实现，但是这样的时间复杂度将会是两次的O(log n)，因此我们可以直接将堆顶元素替换以后执行sift down操作，这样时间复杂度就只有O(log n)。

Replace代码实现

/** * 取出堆中最大元素，并且替换成元素e * @param e * @return */ public E replace(E e){ //获取堆中的最大值 E ret = findMax(); //用新添加的元素替换最大的元素 data.set(0, e); //0索引元素比左右孩子节点元素小，则交换位置，不断循环 siftDown(0); return ret; }

3.6 Heapify操作

Heapify是指将数组转化为堆。

 

这里我们先将数组直接看成是一个完全二叉树，然后找到这棵二叉树的最后一个非叶子节点的节点，也就是该树的最后一个节点的父节点。然后从这个节点开始到根节点结束，执行sift down操作。这样的时间复杂度为O(n)。

Heapify代码实现

/** * 将任意数组整理成堆的形状 * @param arr */ public MaxHeap(E[] arr){ data = new Array<>(arr); //从最后一个叶子节点的父节点开始进行siftDown操作,不断循环 for(int i = parent(arr.length - 1); i >= 0; i --){ siftDown(i); } }

至此就完成了整个基于动态数组实现的最大堆的全部代码，完整代码如下 :

动态数组底层实现

/** * @Author: huangyibo * @Date: 2021/12/25 17:29 * @Description: 数组实现 */ public class Array<E> { private E[] data; private int size; public Array(){ this(10); } public Array(int capacity){ this.data = (E[]) new Object[capacity]; this.size = 0; } public Array(E[] arr){ this.data = (E[]) new Object[arr.length]; for (int i = 0; i < arr.length; i++) { data[i] = arr[i]; } this.size = arr.length; } /** * 获取数组中元素个数 * @return */ public int getSize(){ return size; } /** * 获取数组容量 * @return */ public int getCapacity(){ return data.length; } /** * 返回数组是否为空 * @return */ public boolean isEmpty(){ return size == 0; } /** * 数组尾部新增元素 * @param e */ public void addLast(E e){ add(size, e); } /** * 数组头部新增元素 * @param e */ public void addFirst(E e){ add(0, e); } /** * 在指定位置插入元素 * @param index * @param e */ public void add(int index, E e){ if(index < 0 || index > size){ throw new IllegalArgumentException("AddLast failed. require index >=0 and index <= size"); } if(size == data.length){ //扩容 resize(2 * data.length); } for(int i = size - 1; i >= index; i --){ data[i + 1] = data[i]; } data[index] = e; size ++; } /** * 数组扩容 * @param newCapacity */ private void resize(int newCapacity){ E[] newData = (E[])new Object[newCapacity]; for (int i = 0; i < size; i++) { newData[i] = data[i]; } data = newData; } /** * 获取指定索引位置的值 * @param index * @return */ public E get(int index){ if(index < 0 || index >= size){ throw new IllegalArgumentException("Get failed. index is illegal."); } return data[index]; } /** * 替换指定索引位置的值 * @param index * @param e */ public void set(int index, E e){ if(index < 0 || index >= size){ throw new IllegalArgumentException("Set failed. index is illegal."); } data[index] = e; } /** * 数组是否包含元素e * @param e * @return */ public boolean contains(E e){ for (int i = 0; i < size; i++) { if(data[i].equals(e)){ return true; } } return false; } /** * 查找数组中元素e所在的索引,不存在元素e,返回-1 * @param e * @return */ public int find(E e){ for (int i = 0; i < size; i++) { if(data[i].equals(e)){ return i; } } return -1; } /** * 删除数组中index位置的元素, 并返回删除的元素 * @param index * @return */ public E remove(int index){ if(index < 0 || index >= size){ throw new IllegalArgumentException("Remove failed. index is illegal."); } E ret = data[index]; for (int i = index; i < size - 1; i++) { data[i] = data[i + 1]; } size --; data[size] = null; if(size == data.length / 4 && data.length / 2 != 0){ //当数组长度缩小为原数组的4分之一的时候才进行数组的缩容， //缩小为原数组的2分之一，预留空间，防止有数据添加导致扩容浪费性能 resize(data.length / 2); } return ret; } /** * 删除数组中第一个元素 * @return */ public E removeFirst(){ return remove(0); } /** * 删除数组中最后一个元素 * @return */ public E removeLast(){ return remove(size - 1); } /** * 从数组中删除元素e * @param e */ public void removeElement(E e){ int index = find(e); if(index != -1){ remove(index); } } /** * 数组索引元素交换 * @param i * @param j */ public void swap(int i, int j){ if(i < 0 || i >= size || j < 0 || j >= size){ throw new IllegalArgumentException("Index is illegal."); } E temp = data[i]; data[i] = data[j]; data[j] = temp; } @Override public String toString(){ StringBuilder sb = new StringBuilder(); sb.append(String.format("Array: size = %d, capacity = %d\n",size,data.length)); sb.append("["); for (int i = 0; i < size; i++) { sb.append(data[i]); if(i != size - 1){ sb.append(", "); } } sb.append("]"); return sb.toString(); } }

基于动态数组底层实现的最大堆实现

/** * @Author: huangyibo * @Date: 2022/2/17 22:54 * @Description: 最大堆 完全二叉树，父亲节点大于等于孩子节点，采用数组表示 */ public class MaxHeap<E extends Comparable<E>> { //这里使用数组来实现 private Array<E> data; public MaxHeap(){ data = new Array<>(); } public MaxHeap(int capacity){ data = new Array<>(capacity); } /** * 将任意数组整理成堆的形状 * @param arr */ public MaxHeap(E[] arr){ data = new Array<>(arr); //从最后一个叶子节点的父节点开始进行siftDown操作,不断循环 for(int i = parent(arr.length - 1); i >= 0; i --){ siftDown(i); } } /** * 返回堆中的元素个数 * @return */ public int getSize(){ return data.getSize(); } /** *堆是否为空 * @return */ public boolean isEmpty(){ return data.isEmpty(); } /** * 返回完全二叉树的数组表示中，一个索引所表示的元素的父亲节点的索引 * @param index * @return */ private int parent(int index){ if(index == 0){ throw new IllegalArgumentException("index-0 doesn't have parent."); } return (index - 1) / 2; } /** * 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引 * @return */ private int leftChild(int index){ return index * 2 + 1; } /** * 回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引 * @param index * @return */ private int rightChild(int index){ return index * 2 + 2; } /** * 向堆中添加元素 * @param e */ public void add(E e){ data.addLast(e); //当前元素在数组中的索引为 data.getSize() - 1 //比较当前元素和其父亲节点的元素，大于父亲节点元素则交换位置 siftUp(data.getSize() - 1); } /** * k索引元素比父节点元素大，则交换位置，不断循环 * @param k */ private void siftUp(int k){ //k > 0 并且k索引元素比父节点元素大，则交换位置，不断循环 while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0){ data.swap(parent(k), k); k = parent(k); } } /** * 查看堆中最大元素 * @return */ public E findMax(){ if(data.getSize() == 0){ throw new IllegalArgumentException("Can not findMax when heap is empty."); } return data.get(0); } /** * 取出堆中最大元素 * @return */ public E extractMax(){ //获取堆中最大元素 E ret = findMax(); //堆中最开始的元素和最后元素交换位置 data.swap(0,data.getSize() - 1); //删除堆中最后一个元素 data.removeLast(); //0索引元素比左右孩子节点元素小，则交换位置，不断循环 siftDown(0); return ret; } /** * k索引元素比左右孩子节点元素小，则交换位置，不断循环 * @param k */ private void siftDown(int k){ while (leftChild(k) < data.getSize()){ //获取k索引的左孩子的索引 int j = leftChild(k); //j + 1 < data.getSize() if(j + 1 < data.getSize() && //如果右孩子比左孩子大 data.get(j + 1).compareTo(data.get(j)) > 0){ //最大孩子的索引赋值给j j = rightChild(k); } //此时data[j]是leftChild和rightChild中的最大值 if(data.get(k).compareTo(data.get(j)) >= 0){ //如果父亲节点大于等于左右孩子节点，跳出循环 break; } //如果父亲节点小于左右孩子节点(中的最大值)，交换索引的值 data.swap(k, j); //交换完成之后，将j赋值给K,重新进入循环 k = j; } } /** * 取出堆中最大元素，并且替换成元素e * @param e * @return */ public E replace(E e){ //获取堆中的最大值 E ret = findMax(); //用新添加的元素替换最大的元素 data.set(0, e); //0索引元素比左右孩子节点元素小，则交换位置，不断循环 siftDown(0); return ret; } }

参考： https://www.cnblogs.com/youch/p/10341675.html

https://blog.csdn.net/love905661433/article/details/82989404

https://blog.csdn.net/weixin_39084521/article/details/90322548