归并排序（Merge Sort）

一、算法概述

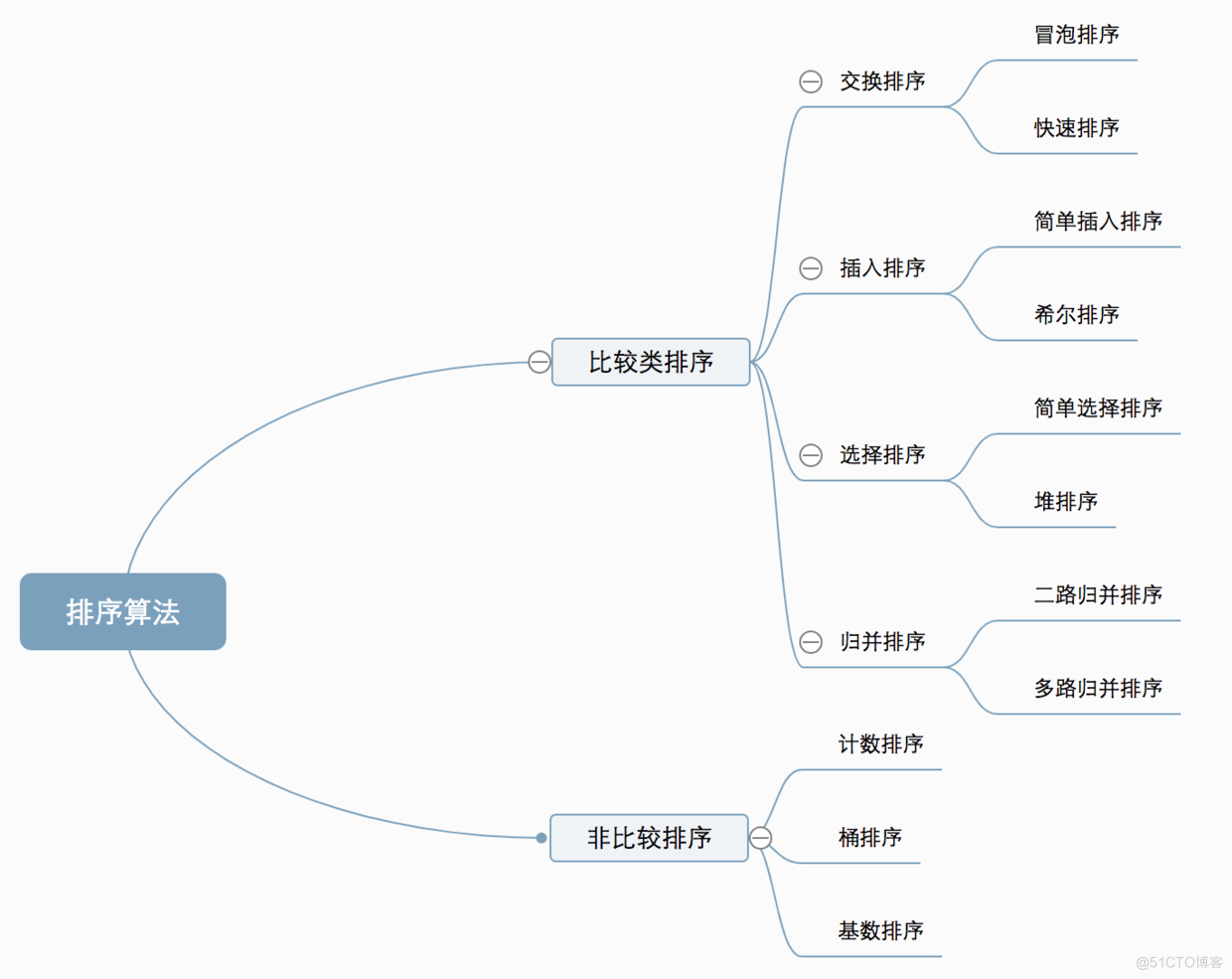
1.1 算法分类

十种常见排序算法可以分为两大类：

• 比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。

• 非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

1.2 算法复杂度

1.3 相关概念

• 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
• 不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。
• 时间复杂度：对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。
• 空间复杂度：是指算法在计算机内执行时所需存储空间的度量，它也是数据规模n的函数。

二、归并排序（Merge Sort）

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

2.1 算法描述

• 把长度为n的输入序列分成两个长度为n/2的子序列；
• 对这两个子序列分别采用归并排序；
• 将两个排序好的子序列合并成一个最终的排序序列。

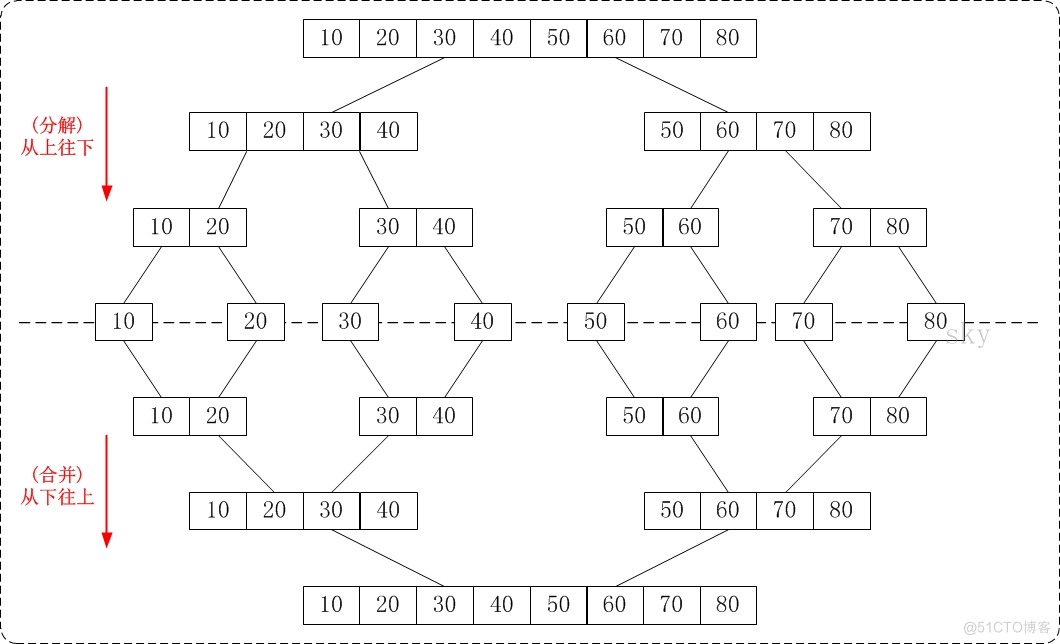
将两个的有序数列合并成一个有序数列，我们称之为"归并"。 归并排序(Merge Sort)就是利用归并思想对数列进行排序。根据具体的实现，归并排序包括"从上往下"和"从下往上"2种方式。

• 1、从下往上的归并排序：将待排序的数列分成若干个长度为1的子数列，然后将这些数列两两合并；得到若干个长度为2的有序数列，再将这些数列两两合并；得到若干个长度为4的有序数列，再将它们两两合并；直接合并成一个数列为止。这样就得到了我们想要的排序结果。(参考下面的图片)

• 2、从上往下的归并排序：它与"从下往上"在排序上是反方向的。它基本包括3步：

  • ① 分解：将当前区间一分为二，即求分裂点 mid = (low + high)/2;
  • ② 求解：递归地对两个子区间a[low...mid] 和 a[mid+1...high]进行归并排序。递归的终结条件是子区间长度为1。
  • ③ 合并：将已排序的两个子区间a[low...mid]和 a[mid+1...high]归并为一个有序的区间a[low...high]。

下面的图片很清晰的反映了"从下往上"和"从上往下"的归并排序的区别。

2.2 动图演示

2.3 归并排序图文说明

从上往下的归并排序采用了递归的方式实现。它的原理非常简单，如下图：

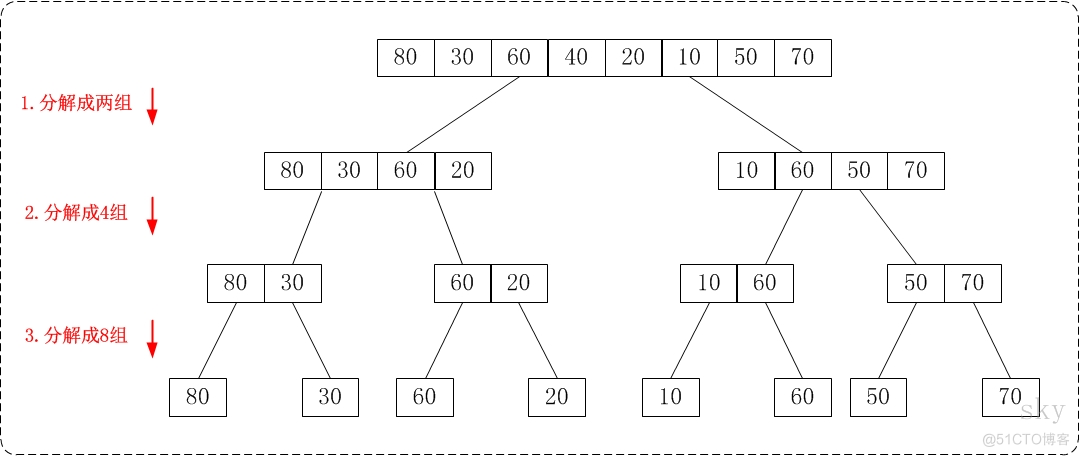
通过"从上往下的归并排序"来对数组{80,30,60,40,20,10,50,70}进行排序时：

• 1、将数组{80,30,60,40,20,10,50,70}看作由两个有序的子数组{80,30,60,40}和{20,10,50,70}组成。对两个有序子树组进行排序即可。
• 2、将子数组{80,30,60,40}看作由两个有序的子数组{80,30}和{60,40}组成。 将子数组{20,10,50,70}看作由两个有序的子数组{20,10}和{50,70}组成。
• 3、将子数组{80,30}看作由两个有序的子数组{80}和{30}组成。 将子数组{60,40}看作由两个有序的子数组{60}和{40}组成。 将子数组{20,10}看作由两个有序的子数组{20}和{10}组成。 将子数组{50,70}看作由两个有序的子数组{50}和{70}组成。

从下往上的归并排序的思想正好与"从上往下的归并排序"相反。如下图：

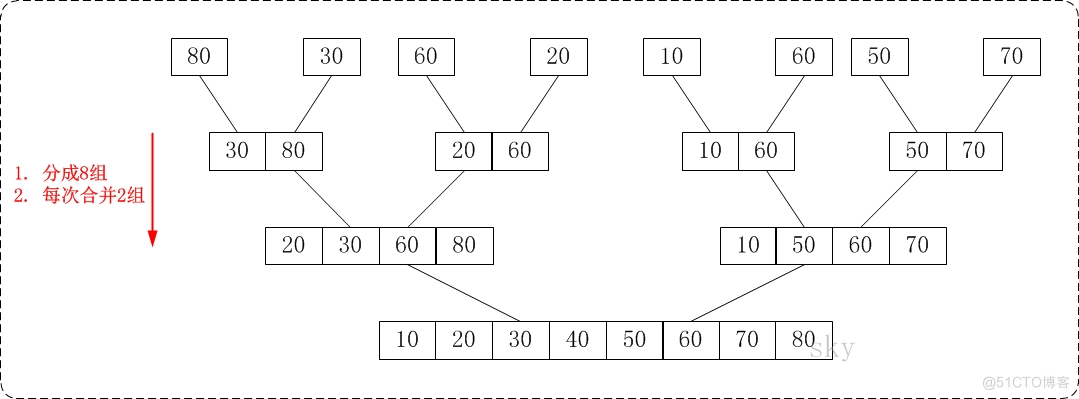
通过"从下往上的归并排序"来对数组{80,30,60,40,20,10,50,70}进行排序时：

• 1、将数组{80,30,60,40,20,10,50,70}看作由8个有序的子数组{80},{30},{60},{40},{20},{10},{50}和{70}组成。
• 2、将这8个有序的子数列两两合并。得到4个有序的子树列{30,80},{40,60},{10,20}和{50,70}。
• 3、将这4个有序的子数列两两合并。得到2个有序的子树列{30,40,60,80}和{10,20,50,70}。
• 4、将这2个有序的子数列两两合并。得到1个有序的子树列{10,20,30,40,50,60,70,80}。

2.4、归并排序的时间复杂度和稳定性

归并排序时间复杂度

归并排序的时间复杂度是O(n㏒n)。 假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢？ 归并排序的形式就是一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的可以得出它的时间复杂度是O(n㏒n)。

归并排序稳定性

归并排序是稳定的算法，它满足稳定算法的定义。 算法稳定性 -- 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

2.5、归并排序代码实现

归并排序(从上往下)

/** * @Author: huangyibo * @Date: 2022/1/16 16:49 * @Description: 归并排序(从上往下) */ public class MergeSort { public static <E extends Comparable<E>> void mergeSort(E[] arr){ if(arr == null){ return; } sort(arr,0,arr.length-1); } /** * 对数组进行分解，排序并归并 * @param arr 待排序的数组 * @param left 数组的起始地址 * @param right 数组的结束地址 * @param <E> 泛型 */ private static <E extends Comparable<E>> void sort(E[] arr, int left, int right){ //如果left >= right则停止分解 if(left >= right){ return; } //对 left和 right 进行对半分解 int mid = (left + right) >>> 1; //对left和mid区间进行二分分解 sort(arr, left, mid); //对mid + 1和right区间进行二分分解 sort(arr,mid + 1, right); if(arr[mid].compareTo(arr[mid + 1]) > 0) { //归并并排序 arr[left, mid] 和 arr[mid+1, right]两个区间 merge(arr, left, mid, right); } } /** * 归并 * 合并两个区间 arr[left, mid] 和arr[mid+1, right] * @param arr 包含两个有序区间的数组 * @param left 第1个有序区间的起始地址 * @param mid 第1个有序区间的结束地址。也是第2个有序区间的起始地址 * @param right 第2个有序区间的结束地址 * @param <E> */ private static <E extends Comparable<E>> void merge(E[] arr, int left, int mid, int right){ //使用临时数组辅助进行数组顺序的归并 E[] temp = Arrays.copyOf(arr, arr.length); int i = left; int j = mid + 1; //每轮循环对arr[k]进行赋值 for(int k = left; k <= right; k++){ //主要就是比较temp[i]和temp[j]的值大小，进行调整 if(i > mid){ //如果i大于mid，直接归并temp[j,right]区间的元素到arr arr[k] = temp[j - left]; j++; }else if(j > right){ //如果j大于right，直接归并temp[i,mid]区间的元素到arr arr[k] = temp[i - left]; i ++; }else if(temp[i - left].compareTo(temp[j - left]) <= 0) { //如果temp[i]小于等于temp[j]，直接归并temp[i]的值到arr arr[k] = temp[i - left]; i ++; }else { //如果temp[i]大于temp[j]，直接归并temp[j]的值到arr arr[k] = temp[j - left]; j++; } } } }

归并排序(从上往下)——采用插入排序优化

• 如果待分解排序归并的区间小于特定的值。
• 停止分解，采用插入排序优化。
• 因为待分解排序归并的区间比较小，使用归并排序反而更耗时。
• 不同的计算机硬件配置，效果不一样，可能优化后性能更低。

/** * @Author: huangyibo * @Date: 2022/1/16 16:49 * @Description: 归并排序(从上往下) 采用插入排序优化 */ public class MergeSort { public static <E extends Comparable<E>> void mergeSort(E[] arr){ if(arr == null){ return; } sort(arr,0,arr.length-1); } /** * 对数组进行分解，排序并归并 * @param arr 待排序的数组 * @param left 数组的起始地址 * @param right 数组的结束地址 * @param <E> 泛型 */ private static <E extends Comparable<E>> void sort(E[] arr, int left, int right){ //如果待分解排序归并的区间小于特定的值， //停止分解，采用插入排序优化 //因为待分解排序归并的区间比较小，使用归并排序反而更耗时 //不同的计算机硬件配置，效果不一样，可能优化后性能更低 if((right - left) <= 15){ InsertionSort.insertionSort(arr, left, right); return; } //对 left和 right 进行对半分解 int mid = (left + right) >>> 1; //对left和mid区间进行二分分解 sort(arr, left, mid); //对mid + 1和right区间进行二分分解 sort(arr,mid + 1, right); if(arr[mid].compareTo(arr[mid + 1]) > 0) { //归并并排序 arr[left, mid] 和 arr[mid+1, right]两个区间 merge(arr, left, mid, right); } } /** * 归并 * 合并两个区间 arr[left, mid] 和arr[mid+1, right] * @param arr 包含两个有序区间的数组 * @param left 第1个有序区间的起始地址 * @param mid 第1个有序区间的结束地址。也是第2个有序区间的起始地址 * @param right 第2个有序区间的结束地址 * @param <E> */ private static <E extends Comparable<E>> void merge(E[] arr, int left, int mid, int right){ //使用临时数组辅助进行数组顺序的归并 E[] temp = Arrays.copyOf(arr, arr.length); int i = left; int j = mid + 1; //每轮循环对arr[k]进行赋值 for(int k = left; k <= right; k++){ //主要就是比较temp[i]和temp[j]的值大小，进行调整 if(i > mid){ //如果i大于mid，直接归并temp[j,right]区间的元素到arr arr[k] = temp[j - left]; j++; }else if(j > right){ //如果j大于right，直接归并temp[i,mid]区间的元素到arr arr[k] = temp[i - left]; i ++; }else if(temp[i - left].compareTo(temp[j - left]) <= 0) { //如果temp[i]小于等于temp[j]，直接归并temp[i]的值到arr arr[k] = temp[i - left]; i ++; }else { //如果temp[i]大于temp[j]，直接归并temp[j]的值到arr arr[k] = temp[j - left]; j++; } } } } /** * @Author: huangyibo * @Date: 2021/12/24 0:30 * @Description: 插入排序(归并排序的优化使用版本) */ public class InsertionSort { /** * 对数组特定的区间进行排序，归并排序的优化使用版本 * @param arr 待排序的数组 * @param left 待排序的数组的起始位置 * @param right 待排序数组的结束位置 * @param <E> 泛型 */ public static <E extends Comparable<E>> void insertionSort(E[] arr,int left, int right){ //i代表待插入元素的索引 for (int i = left; i <= right; i++) { //代表待插入的元素值 E temp = arr[i]; //j 代表已排序区域的元素索引 int j; for (j = i; j > 0; j--) { if(temp.compareTo(arr[j - 1]) < 0){ //将arr[j]插到合适的位置 arr[j] = arr[j - 1]; }else { //退出循环，减少比较次数 break; } } arr[j] = temp; } } }

归并排序(从上往下)——内存优化——推荐方式

• 使用公共的临时数组空间，辅助进行数组顺序的归并，merge()方法专用，性能优化巨大。

/** * @Author: huangyibo * @Date: 2022/1/16 16:49 * @Description: 归并排序(从上往下) 内存优化 */ public class MergeSort { public static <E extends Comparable<E>> void mergeSort(E[] arr){ if(arr == null){ return; } //使用公共的临时数组辅助进行数组顺序的归并 merge()方法专用 E[] temp = Arrays.copyOf(arr, arr.length); sort(arr,0,arr.length-1,temp); } /** * 对数组进行分解，排序并归并 * @param arr 待排序的数组 * @param left 数组的起始地址 * @param right 数组的结束地址 * @param temp merge()方法专用, 公共的临时空间，辅助进行数组顺序的归并 * @param <E> 泛型 */ private static <E extends Comparable<E>> void sort(E[] arr, int left, int right, E[] temp){ //如果left >= right则停止分解 if(left >= right){ return; } //对 left和 right 进行对半分解 int mid = (left + right) >>> 1; //对left和mid区间进行二分分解 sort(arr, left, mid, temp); //对mid + 1和right区间进行二分分解 sort(arr,mid + 1, right, temp); if(arr[mid].compareTo(arr[mid + 1]) > 0) { //归并并排序 arr[left, mid] 和 arr[mid+1, right]两个区间 merge(arr, left, mid, right, temp); } } /** * 归并 * 合并两个区间 arr[left, mid] 和arr[mid+1, right] * @param arr 包含两个有序区间的数组 * @param left 第1个有序区间的起始地址 * @param mid 第1个有序区间的结束地址。也是第2个有序区间的起始地址 * @param right 第2个有序区间的结束地址 * @param temp 公共的临时空间，辅助进行数组顺序的归并 * @param <E> */ private static <E extends Comparable<E>> void merge(E[] arr, int left, int mid, int right, E[] temp){ //将arr数组从left位置开始拷贝到temp数组的left位置开始 //拷贝right - left + 1个元素，(前闭后开，所以要 + 1) //因为没有额外的内存开辟，性能优化很高 System.arraycopy(arr, left, temp, left,right - left + 1); int i = left; int j = mid + 1; //每轮循环对arr[k]进行赋值 for(int k = left; k <= right; k++){ //主要就是比较temp[i]和temp[j]的值大小，进行调整 if(i > mid){ //如果i大于mid，直接归并temp[j,right]区间的元素到arr arr[k] = temp[j]; j++; }else if(j > right){ //如果j大于right，直接归并temp[i,mid]区间的元素到arr arr[k] = temp[i]; i ++; }else if(temp[i].compareTo(temp[j]) <= 0) { //如果temp[i]小于等于temp[j]，直接归并temp[i]的值到arr arr[k] = temp[i]; i ++; }else { //如果temp[i]大于temp[j]，直接归并temp[j]的值到arr arr[k] = temp[j]; j++; } } } }

归并排序(从下往上)

/** * @Author: huangyibo * @Date: 2022/1/16 16:49 * @Description: 归并排序(从下往上) */ public class MergeSort2 { public static <E extends Comparable<E>> void mergeSort(E[] arr){ if(arr == null){ return; } //从1开始，按2的倍数进行分解 for (int i = 1; i < arr.length; i *= 2) { mergeGroups(arr, arr.length, i); } } /** * 对数组arr做若干次合并：数组a的总长度为len，将它分为若干个长度为gap的子数组 * 将"每2个相邻的子数组" 进行合并排序。 * @param arr 待排序的数组 * @param len 数组的长度 * @param gap 子数组的长度 * @param <E> 泛型 */ private static <E extends Comparable<E>> void mergeGroups(E[] arr, int len, int gap){ int i; int twoLen = 2 * gap; // 两个相邻的子数组的长度 // 将"每2个相邻的子数组" 进行合并排序。 for(i = 0; i + twoLen - 1 < len; i += twoLen){ merge(arr, i, i + gap - 1, i + twoLen - 1); } // 若 i + gap-1 < len-1，则剩余一个子数组没有配对。 // 将该子数组合并到已排序的数组中。 if (i + gap - 1 < len - 1){ merge(arr, i, i + gap - 1, len - 1); } } /** * 归并 * 合并两个区间 arr[left, mid] 和arr[mid+1, right] * @param arr 包含两个有序区间的数组 * @param left 第1个有序区间的起始地址 * @param mid 第1个有序区间的结束地址。也是第2个有序区间的起始地址 * @param right 第2个有序区间的结束地址 * @param <E> */ private static <E extends Comparable<E>> void merge(E[] arr, int left, int mid, int right){ //使用临时数组辅助进行数组顺序的归并 E[] temp = Arrays.copyOf(arr, arr.length); int i = left; int j = mid + 1; //每轮循环对arr[k]进行赋值 for(int k = left; k <= right; k++){ //主要就是比较temp[i]和temp[j]的值大小，进行调整 if(i > mid){ //如果i大于mid，直接归并temp[j,right]区间的元素到arr arr[k] = temp[j - left]; j++; }else if(j > right){ //如果j大于right，直接归并temp[i,mid]区间的元素到arr arr[k] = temp[i - left]; i ++; }else if(temp[i - left].compareTo(temp[j - left]) <= 0) { //如果temp[i]小于等于temp[j]，直接归并temp[i]的值到arr arr[k] = temp[i - left]; i ++; }else { //如果temp[i]大于temp[j]，直接归并temp[j]的值到arr arr[k] = temp[j - left]; j++; } } } }

归并排序(从下往上)——推荐方式

• 使用公共的临时数组空间，辅助进行数组顺序的归并，merge()方法专用，性能优化巨大。

/** * @Author: huangyibo * @Date: 2022/1/16 16:49 * @Description: 归并排序(从下往上) */ public class MergeSort5 { public static <E extends Comparable<E>> void mergeSort(E[] arr){ if(arr == null){ return; } //使用公共的临时数组辅助进行数组顺序的归并 merge()方法专用 E[] temp = Arrays.copyOf(arr, arr.length); //从1开始，按2的倍数进行分解 for (int sz = 1; sz < arr.length; sz *= 2) { //内层循环 从0出发，每一轮按两个sz区间的增长遍历合并，即起始位置为i //合并 [i, i + sz - 1] 和 [i + sz, Math.min(i + sz + sz - 1, arr.length - 1)] 区间的元素 for (int i = 0; i + sz < arr.length; i += sz + sz){ //i += sz + sz 即i按sz的2倍递增 //i + sz < arr.length 说明后面的区间还有元素,后面的区间有元素，则就要和前面的区间进行合并 if(arr[i + sz - 1].compareTo(arr[i + sz]) > 0){ //注意 i + sz + sz - 1有可能会越界，所以使用Math.min(i + sz + sz - 1, arr.length - 1) merge(arr, i, i + sz - 1, Math.min(i + sz + sz - 1, arr.length - 1) ,temp); } } } } /** * 归并 * 合并两个区间 arr[left, mid] 和arr[mid+1, right] * @param arr 包含两个有序区间的数组 * @param left 第1个有序区间的起始地址 * @param mid 第1个有序区间的结束地址。也是第2个有序区间的起始地址 * @param right 第2个有序区间的结束地址 * @param temp 公共的临时空间，辅助进行数组顺序的归并 * @param <E> 泛型 */ private static <E extends Comparable<E>> void merge(E[] arr, int left, int mid, int right, E[] temp){ //将arr数组从left位置开始拷贝到temp数组的left位置开始 //拷贝right - left + 1个元素，(前闭后开，所以要 + 1) //因为没有额外的内存开辟，性能优化很高 System.arraycopy(arr, left, temp, left,right - left + 1); int i = left; int j = mid + 1; //每轮循环对arr[k]进行赋值 for(int k = left; k <= right; k++){ //主要就是比较temp[i]和temp[j]的值大小，进行调整 if(i > mid){ //如果i大于mid，直接归并temp[j,right]区间的元素到arr arr[k] = temp[j]; j++; }else if(j > right){ //如果j大于right，直接归并temp[i,mid]区间的元素到arr arr[k] = temp[i]; i ++; }else if(temp[i].compareTo(temp[j]) <= 0) { //如果temp[i]小于等于temp[j]，直接归并temp[i]的值到arr arr[k] = temp[i]; i ++; }else { //如果temp[i]大于temp[j]，直接归并temp[j]的值到arr arr[k] = temp[j]; j++; } } } }

参考： https://www.cnblogs.com/onepixel/articles/7674659.html

https://www.cnblogs.com/skywang12345/p/3602369.html