简介
数组（Array）是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。因此可以通过索引(Index)计算出某个元素的地址。
数组特点
- 索引(即下标) 一般从0开始，如java, C/C++。
- 长度固定，在申请时长度固定。内存连续，在内存中则是申请一块连续的固定大小的空间。
- 数组有一维数组和多维数组，数组元素可以是基本数据类型(Primitive)，也可以是对象引用(Reference)。
- 随机访问，能够根据位置(下标)直接访问到元素。
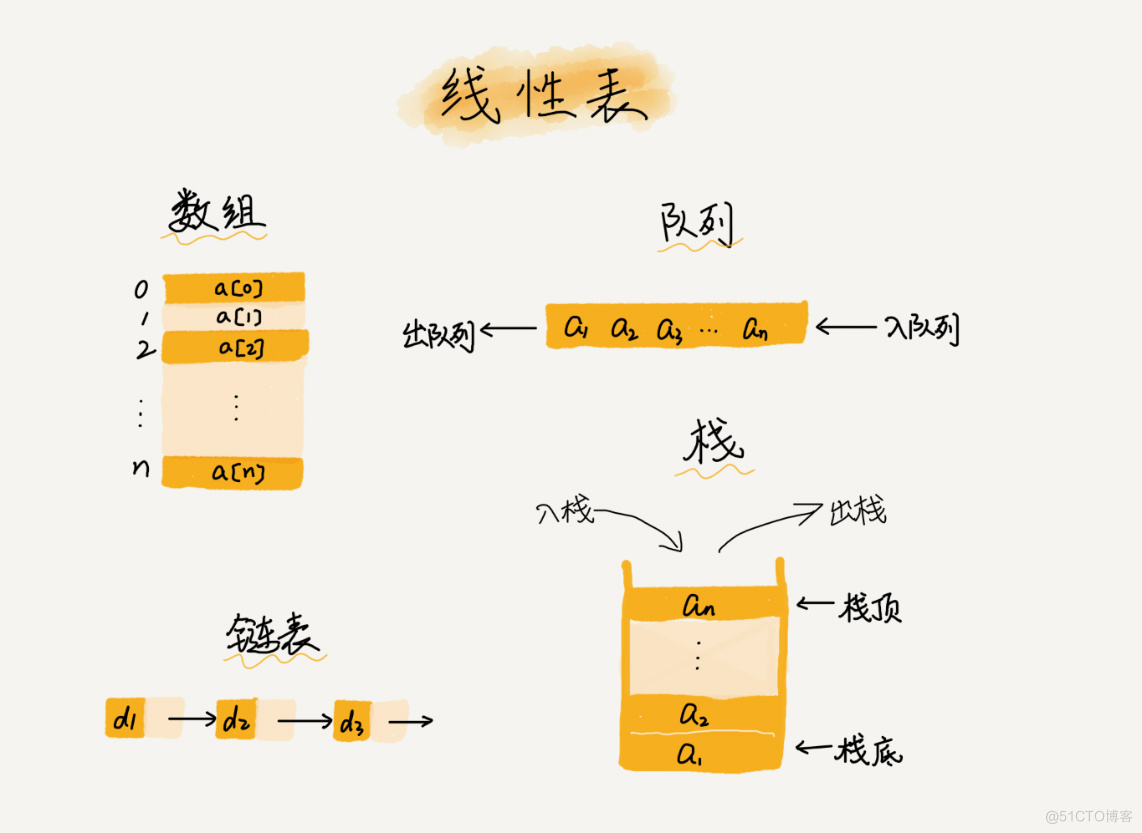
线性表（Linear List）
零个或多个数据元素的有限序列。每个线性表上的数据最多只有前和后两个方向。其实除了数组、链表、队列、栈等也是线性表结构。
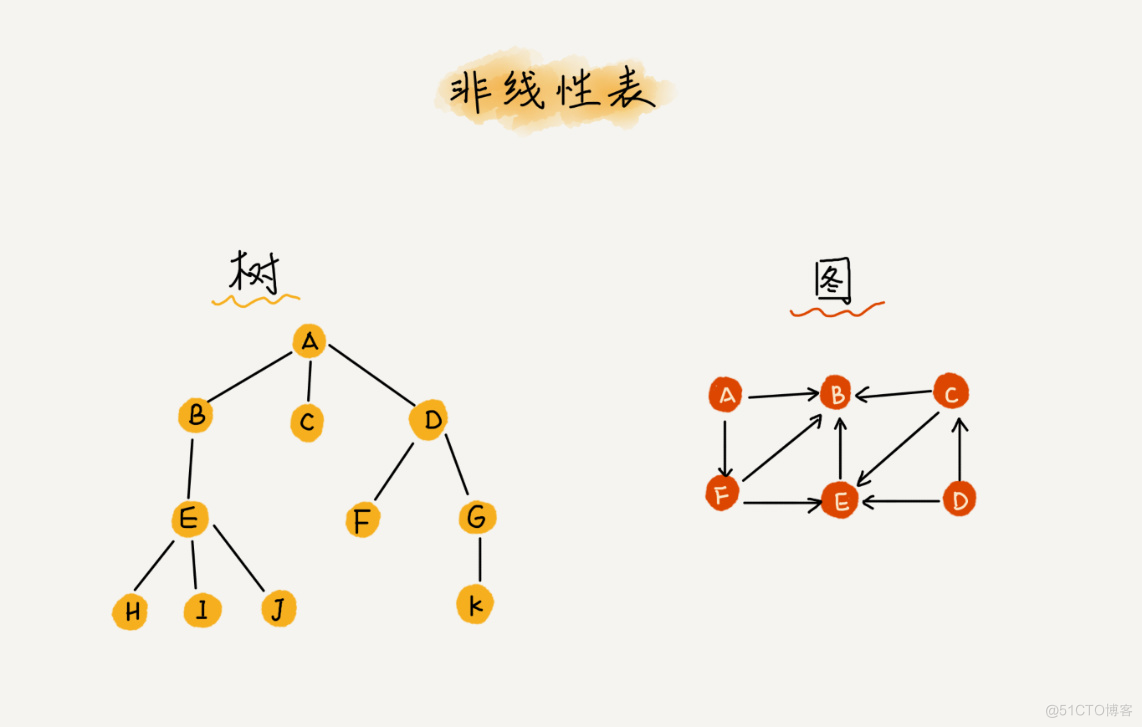
非线性表
它相对立的概念是非线性表，比如二叉树、堆、图等。之所以叫非线性，是因为，在非线性表中，数据之间并不是简单的前后关系。
连续的内存空间和相同类型的数据：这两个限制也让数组的很多操作变得非常低效，比如要想在数组中删除、插入一个数据，为了保证连续性，就需要做大量的数据搬移工作。但是数组的随机访问效率确实十分的高。
插入
假设数组的长度为 n，将一个数据插入到数组中的第 k 个位置。为了把第 k 个 位置腾出来，给新来的数据，我们需要将第 k～n 这部分的元素都顺序地往后挪一位。
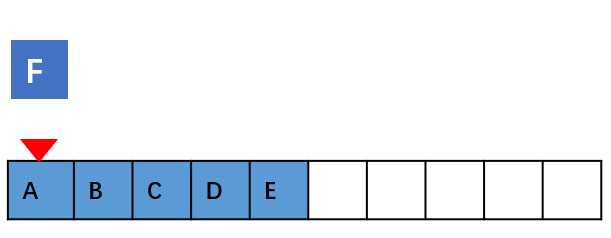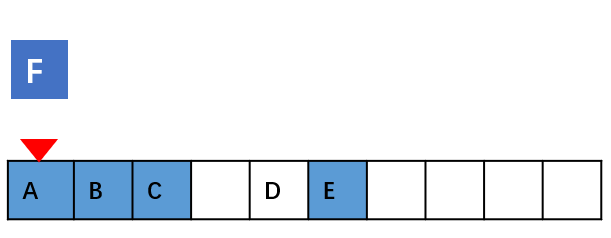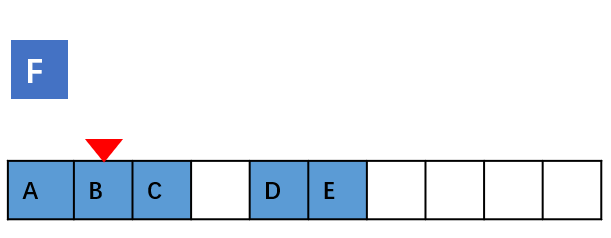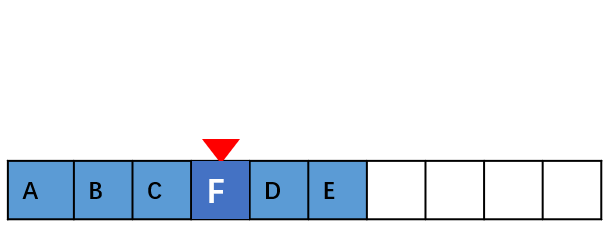
如果在数组的末尾插入元素，那就不需要移动数据了，这时的时间复杂度为 O(1)。
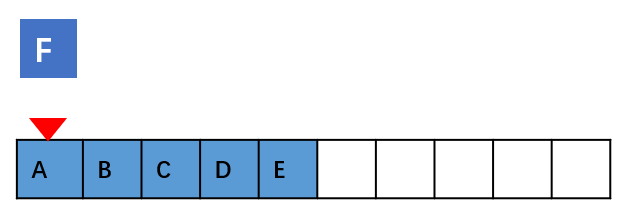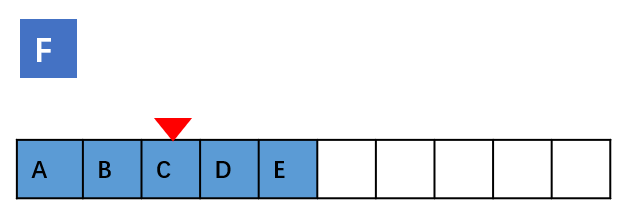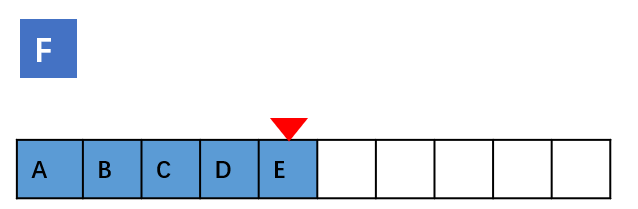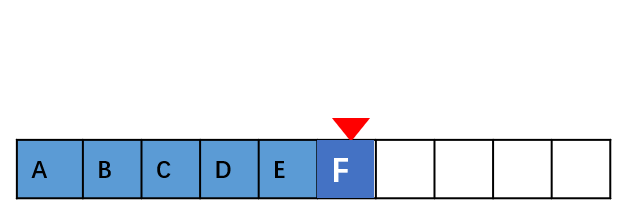
但如果在数组的开头插入元素，那所有的数据都需要依次往后移动一位，所以最坏时间复杂度是 O(n)。 因为我们在 每个位置插入元素的概率是一样的，所以平均情况时间复杂度为 (1+2+…n)/n=O(n)。
如果数组中的数据是有序的，我们在某个位置插入一个新的元素时，就必须按照刚才的方法搬移 k 之后的数据。但是，如果数组中存储的数据并没有任何规律，数组只是被当作一个存储数据的集 合。在这种情况下，如果要将某个数组插入到第 k 个位置，为了避免大规模的数据搬移，我们还有 一个简单的办法就是，直接将第 k 位的数据搬移到数组元素的最后，把新的元素直接放入第 k 个位 置。
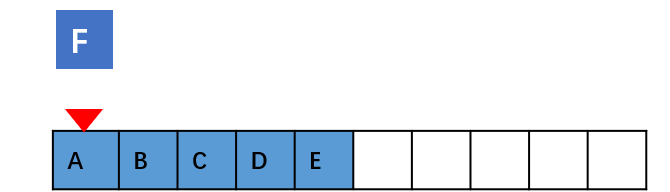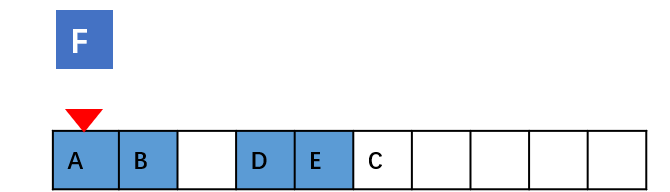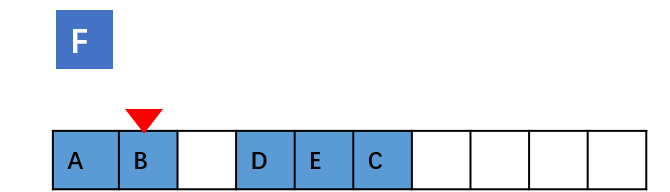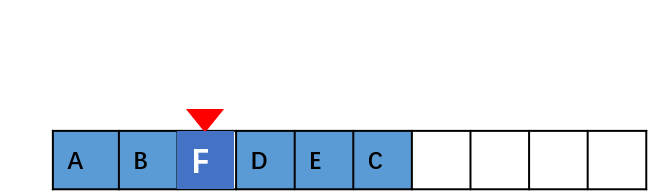在特定场景下，在第 k 个位置插入一个元素的时间复杂度就会降为 O(1)。这个 处理思想在快排中会用。
删除
插入数据类似，我们要删除第 k 个位置的数据，为了内存的连续性，也需要搬移数据，不然中间就会出现空洞，内存就不连续了。在某些特殊场景下，我们并不一定非得追求数组中数据的连续性。如果我们将多次删除操作集中在一起执行，这种就类似于Java虚拟中的标记清除。
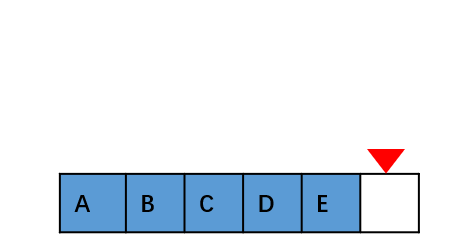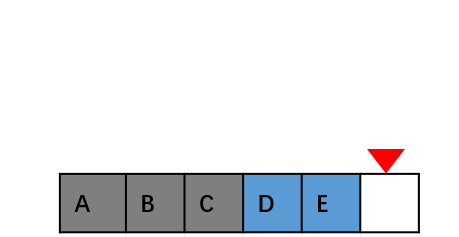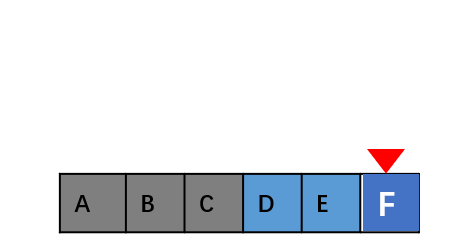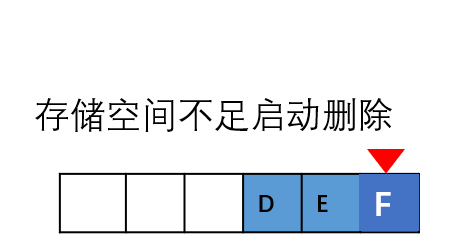
当数组没有更多空间存储数据时，我们再触发执行一次真正的删除操作，这样就大大减少了删除操作导致的数据搬移。
容器
ArrayList 最大的优势就是可以将很多数组操作的细节封装起来。比如前面提到的数组 插入、删除数据时需要搬移其他数据等。
另外，它还有一个优势，就是支持动态扩容。数组本身在定义的时候需要预先指定大小，因为需要分配连续的内存空间。如果我们申请了大小为 10 的数组，当第 11 个数据需要存储到数组中时，我们就需要重新分配一块更大的空间，将原来的 数据复制过去，然后再将新的数据插入。
如果使用 ArrayList，我们就完全不需要关心底层的扩容逻辑，ArrayList 已经帮我们实现好了。每次 存储空间不够的时候，它都会将空间自动扩容为 1.5 倍大小。
不过，这里需要注意一点，因为扩容操作涉及内存申请和数据搬移，是比较耗时的。所以，如果事 先能确定需要存储的数据大小，最好在创建 ArrayList 的时候事先指定数据大小。
比如我们要从数据库中取出 10000 条数据放入 ArrayList。我们看下面这几行代码，你会发现，相比 之下，事先指定数据大小可以省掉很多次内存申请和数据搬移操作。
自定义实现ArrayList
public class Array<E> { private E[] data; private int size; public Array(){ this(10); } public Array(int capacity){ this.data = (E[]) new Object[capacity]; this.size = 0; } /** * 获取数组中元素个数 * @return */ public int getSize(){ return size; } /** * 获取数组容量 * @return */ public int getCapacity(){ return data.length; } /** * 返回数组是否为空 * @return */ public boolean isEmpty(){ return size == 0; } /** * 数组尾部新增元素 * @param e */ public void addLast(E e){ add(size, e); } /** * 数组头部新增元素 * @param e */ public void addFirst(E e){ add(0, e); } /** * 在指定位置插入元素 * @param index * @param e */ public void add(int index, E e){ if(index < 0 || index > size){ throw new IllegalArgumentException("AddLast failed. require index >=0 and index <= size"); } if(size == data.length){ //扩容 resize(2 * data.length); } for(int i = size - 1; i >= index; i --){ data[i + 1] = data[i]; } data[index] = e; size ++; } /** * 数组扩容 * @param newCapacity */ private void resize(int newCapacity){ E[] newData = (E[])new Object[newCapacity]; for (int i = 0; i < size; i++) { newData[i] = data[i]; } data = newData; } /** * 获取指定索引位置的值 * @param index * @return */ public E get(int index){ if(index < 0 || index >= size){ throw new IllegalArgumentException("Get failed. index is illegal."); } return data[index]; } /** * 替换指定索引位置的值 * @param index * @param e */ public void set(int index, E e){ if(index < 0 || index >= size){ throw new IllegalArgumentException("Set failed. index is illegal."); } data[index] = e; } /** * 数组是否包含元素e * @param e * @return */ public boolean contains(E e){ for (int i = 0; i < size; i++) { if(data[i].equals(e)){ return true; } } return false; } /** * 查找数组中元素e所在的索引,不存在元素e,返回-1 * @param e * @return */ public int find(E e){ for (int i = 0; i < size; i++) { if(data[i].equals(e)){ return i; } } return -1; } /** * 删除数组中index位置的元素, 并返回删除的元素 * @param index * @return */ public E remove(int index){ if(index < 0 || index >= size){ throw new IllegalArgumentException("Remove failed. index is illegal."); } E ret = data[index]; for (int i = index; i < size - 1; i++) { data[i] = data[i + 1]; } size --; data[size] = null; if(size == data.length / 4 && data.length / 2 != 0){ //当数组长度缩小为原数组的4分之一的时候才进行数组的缩容， //缩小为原数组的2分之一，预留空间，防止有数据添加导致扩容浪费性能 resize(data.length / 2); } return ret; } /** * 删除数组中第一个元素 * @return */ public E removeFirst(){ return remove(0); } /** * 删除数组中最后一个元素 * @return */ public E removeLast(){ return remove(size - 1); } /** * 从数组中删除元素e * @param e */ public void removeElement(E e){ int index = find(e); if(index != -1){ remove(index); } } @Override public String toString(){ StringBuilder sb = new StringBuilder(); sb.append(String.format("Array: size = %d, capacity = %d\n",size,data.length)); sb.append("["); for (int i = 0; i < size; i++) { sb.append(data[i]); if(i != size - 1){ sb.append(", "); } } sb.append("]"); return sb.toString(); } }测试
public class ArrayDemo1 { public static void main(String[] args) { Array<Integer> array = new Array<Integer>(); for (int i = 0; i < 10; i++) { array.addLast(i); } System.out.println(array); array.add(1,200); System.out.println(array); array.addFirst(-1); System.out.println(array); array.remove(2); System.out.println(array); array.removeElement(4); System.out.println(array); array.removeFirst(); System.out.println(array); array.removeLast(); System.out.println(array); } }时间复杂度总结
最后整理个表格，上述操作的时间复杂度大致如下，很容易理解就不详细解释了。
操作 平均时间复杂度 最坏条件时间复杂度 插入 O(n) O(n) 删除 O(n) O(n) 查找 O(n) O(n) 访问 O(1) O(1)参考： https://blog.csdn.net/weixin_39084521/article/details/89820318
https://www.cnblogs.com/fanglongxiang/p/13034353.html