凸包+最小外接圆
凸包的定义:
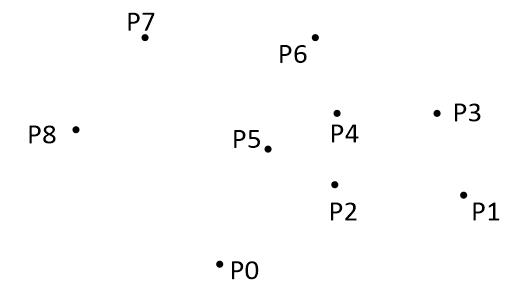
假设平面上有p0~p12共13个点,过某些点作一个多边形,使这个多边形能把所有点都“包”起来。当这个多边形是凸多边形的时候,我们就叫它“凸包”。如下图:
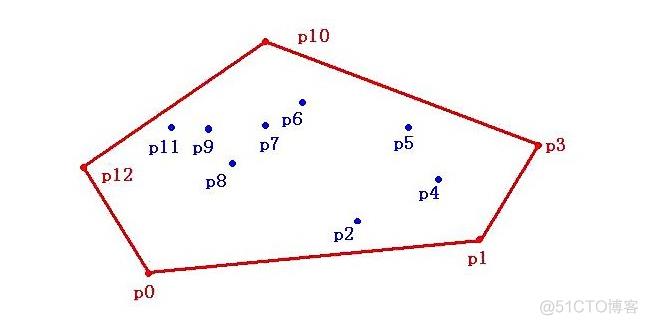
我们把这些点放在二维坐标系里面,那么每个点都能用 (x,y) 来表示。
现给出点的数目13,和各个点的坐标。求构成凸包的点?
题目:HDU2215
说这个题之前,先理解一下凸包和最小外接圆。
凸包问题的五种解法
我觉得最简便的是 Graham扫描法。基本原理如图所示:
先把图理解,原理就是,我们先选出最靠下的那个点(有多个时选靠左的)作为基准点,然后把其他的点排序,排序规则就如同图中前进的方向,从p0向每一个点画一条射线,然后按射线逆时针排序,若有多个点在同一条射线上,距离p0近的排在前面。
然后就是怎么实现。要用到叉乘:
两个向量a , b ,a*b=|a|*|b|*sin(t);
当a*b>0时,即sin>0,此时a,b的夹角为(0,π),也就是 b 在 a 的逆时针方向
当a*b<0时,即sin<0,此时a,b的夹角为(0,-π),也就是 b 在 a 的顺时针方向(可以暂时假设a是x轴,看下图)
把凸包点都求出来以后,要求最小外接圆,三个点确定一个圆,除了点数不够三个外,我们枚举,每次区三个点假设为外接圆上的点,然后用公式计算出半径。
如果这三个点构成钝角三角形,那么最小外接圆应该是以最长边为直径的圆,R=c/2. 如果不是钝角三角形,根据正弦定理a/sinA = b/sinB = c/sinC = 2R,S = bcsinA/2,带入得R = abc/4S,S直接用叉积可以算出来,
也就是S= a*b*sin(t)*1/2;
向量 a(x1, y1) 叉乘 向量 b(x2, y2) = x1*y2 - x2*y1 ;
代码:
#include<stdio.h>
#include<math.h>
#include<stdlib.h>
#include<algorithm>
using namespace std;
struct point{
double x,y;
}p[110],stk[110],base;
int n,top;
double lenth(point a,point b)
{
return sqrt(pow(a.x-b.x,2)+pow(a.y-b.y,2));
}
double fork(point c,point m,point n)//求叉乘
{
return (m.x-c.x)*(n.y-c.y)-(m.y-c.y)*(n.x-c.x);
}
bool cmp(point p1,point p2)
{
if(fork(base,p1,p2)==0)//三点一线
return lenth(base,p1)<lenth(base,p2);//按距离从近到远
return fork(base,p1,p2)>0;
}
bool check(double a,double b,double c)//检查是否钝角三角形
{
if(a*a+b*b<c*c || a*a+c*c<b*b || b*b+c*c<a*a)
return 1;//是钝角三角形
return 0;
}
double R(point p1,point p2,point p3)//计算三角形外接圆半径
{
double a=lenth(p1,p2);
double b=lenth(p2,p3);
double c=lenth(p1,p3);
if(check(a,b,c))//是钝角三角形
return max(a,max(b,c))/2.0;
double s=fabs(fork(p1,p2,p3))/2.0;
return a*b*c/(4.0*s);
}
void getside()//求凸包点,存入数组stk[]
{
top=1;//top始终表示上一个确定下来的点
stk[0]=p[0];
stk[1]=p[1];
for(int i=2;i<n;i++)
{
while(top>0&&fork(stk[top-1],stk[top],p[i])<=0)//上一个确定的点是凹的
top--;
stk[++top]=p[i];
}
}
double every()//对凸包点枚举,每次假设三个点
{
if(top == 1)
return lenth(stk[0], stk[1]) / 2.0 ;
double r=0;
for(int i=0;i<=top;i++)
for(int j=i+1;j<=top;j++)
for(int k=j+1;k<=top;k++)
{
if(r < R(stk[i],stk[j],stk[k]))
r = R(stk[i],stk[j],stk[k]);
}
return r;//得出半径
}
int main()
{
while(scanf("%d",&n),n)
{
base={1000,1000};
int mini=0;
for(int i=0;i<n;i++)
{
scanf("%lf%lf",&p[i].x,&p[i].y);
if(p[i].y<base.y||(p[i].y==base.y&&p[i].x<base.x))
{
base.x=p[i].x;
base.y=p[i].y;
mini=i;
}
}
swap(p[mini],p[0]);
sort(p+1,p+n,cmp);//排序
if(n==1)
{
puts("0.50");
continue;
}
getside();//得出凸包点
double r=every();
printf("%.2lf\n",r+0.5);
}
return 0;
}
求凸包的模板(前提是p已排序):
void getside()//求凸包点,存入数组stk[]
{
top=1;//top始终表示上一个确定下来的点
stk[0]=p[0];
stk[1]=p[1];
for(int i=2;i<n;i++)
{
while(top>0&&fork(stk[top-1],stk[top],p[i])<=0)//上一个确定的点是凹的
top--;
stk[++top]=p[i];
}
}