在关联分析的结果中,对于odd ratio值会给出95% CI的结果,这里的CI其实是confidence interval的缩写,代表置信区间。那么置信区间有什么用呢?
关联分析的核心思想是通过抽样的数据来评估总体的分布,在数学上通过样本统计量来评估总体的参数是一个典型的参数估计问题。对于参数估计,有两大类方法,第一个是点估计,第二个是区间估计。顾名思义,点估计就是给出参数的一个具体数值,区间估计就是给出一个取值的范围,置信区间就属于区间估计。
为什么我们需要区间估计呢?先来看一个例子,随机抽取40名男生来计算男生的平均身高,第一次抽样得到的平均身高是173cm, 第二个抽样平均身高为175cm,很显然,两次抽样对于总体均值的估计存在了波动,每次抽样给出的均值就看做是点估计,可以看出,对于同一个总体,不同抽样实验给出的点估计值存在了波动。这样的情况下,如何来准确描述总体的参数呢?此时就需要区间估计上场了。
不同于点估计,区间估计会给出总体参数分布的一个范围,对应两个值,分别为下限和上限。这两个值如何来确定呢?如果我说男生的平均身高范围在0到正无穷之间,这句话肯定是没有问题的,但是这样没有任何意义,我们需要一个系统的方法和规则,给出有意义的区间范围。
这个方法就是概率,和置信区间伴生的有一个概念,叫做置信水平,也称之为置信度。在描述概率时,我们通常会选定一个显著性水平,比如0.05,而置信度就是1减去显著性水平,所以经常会看到95%的置信度这样的叫法,置信度描述的是总体参数的真实值落在对应置信区间的概率, 以95%置信度为例,代表100次抽样中,其中有95次抽样的置信区间会包含总体参数的真实值。
置信度是计算置信区间的前提,所以在描述置信区间的值时,一定会给出对应的置信度,比如文章开头提到的,95%置信度下的置信区间。置信度根据我们选定的显著性水平来确定,是一个主观选定的数值,通常使用的是95%的置信度。置信度确定了之后,如何来计算置信区间呢?既然涉及到了概率,肯定想要知道总体的分布,以方便我们确定对应的概率密度分布。
根据中心极限定理,抽样个数超过30的情况下,可以用样本均值来表征总体均值,而且总体的数值分布在均值附近呈现正态分布,如下图所示
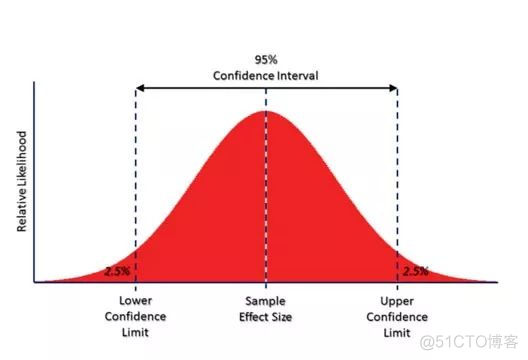
对于任意的正态分布,可以通过Z值将其转换为标准正态分布,公式如下
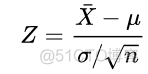
以95%置信度为例,位于置信区间内的概率为95%,则位于其他两侧的概率分别为2.5%,用R计算对应的z值,代码如下

qnorm是累计概率密度函数,四舍五入之后,结果为-1.96和-1.96, 所以经常看到如下所示的图
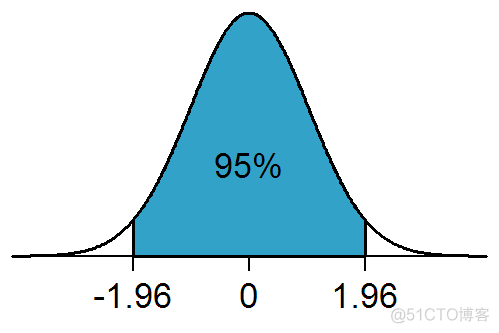
得到z值之后,就可以计算对应的置信区间了,公式如下
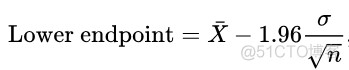
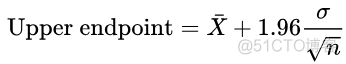
标准差除以样本个数的开方其实就是标准误了,以R语言中的逻辑回归为例
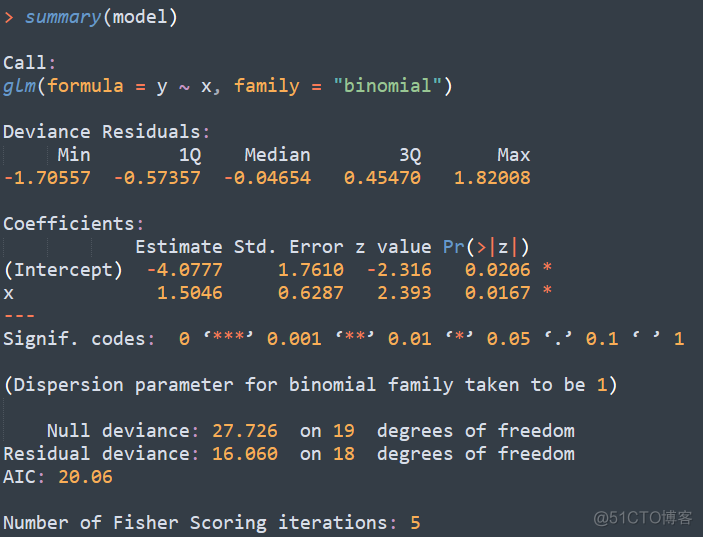
之前的文章介绍过,逻辑回归的OR值就是自变量的回归系数,上述例子中自变量x的回归系数为1.5046,而标准误为0.6287,根据这个结果,我们可以计算出该变量OR值的95%的置信区间
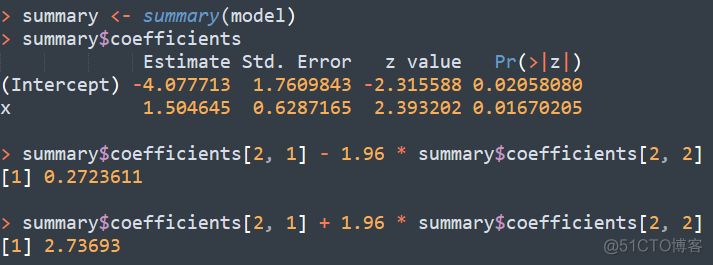
置信区间能够更加准确的描述总体参数的分布情况,在数据分析中广泛使用。
·end·

