一、算法概述 1.1 算法分类 十种常见排序算法可以分为两大类: 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序
一、算法概述
1.1 算法分类
十种常见排序算法可以分为两大类:
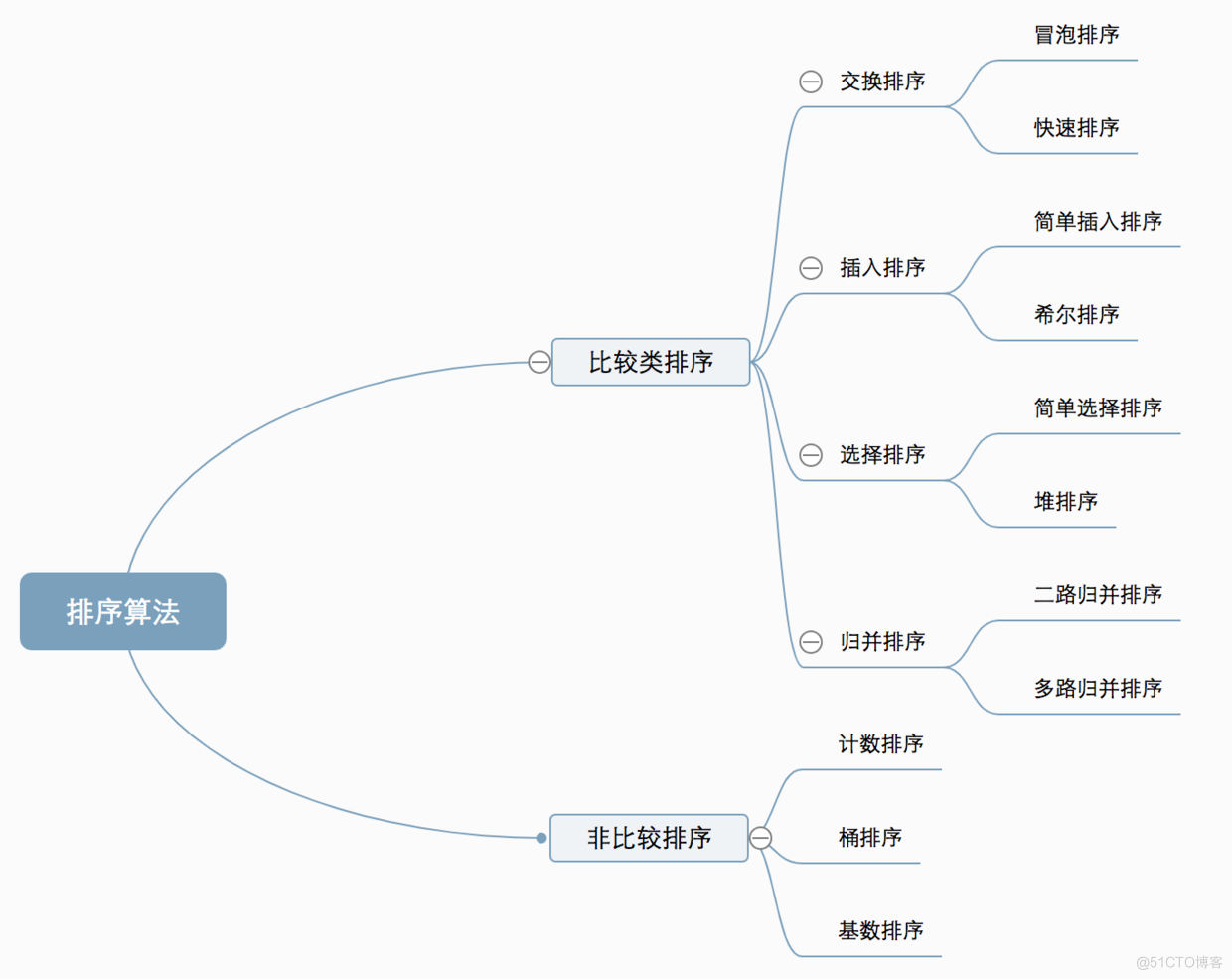
1.2 算法复杂度
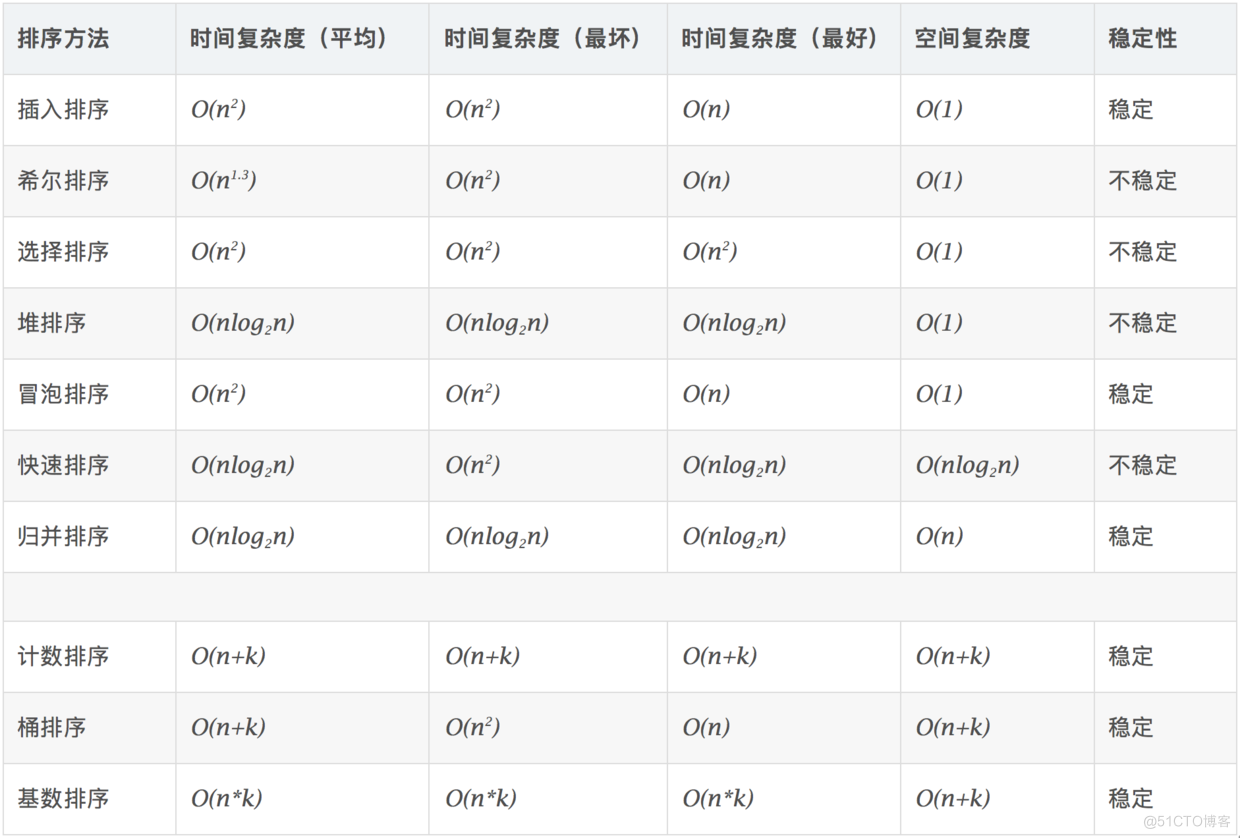
1.3 相关概念
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
- 不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
- 时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
- 空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
二、希尔排序(Shell Sort)
1959年Shell发明,第一个突破O(n²)的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
2.1 算法描述
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
- 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- 按增量序列个数k,对序列进行k 趟排序;
- 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
2.2 动图演示
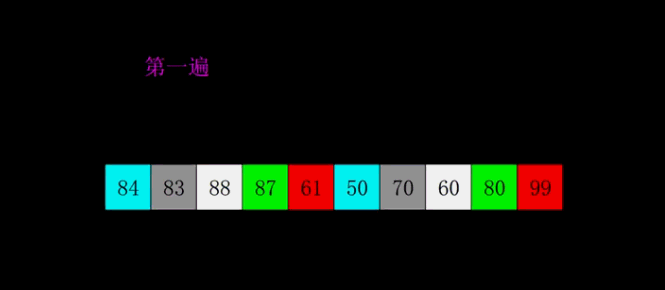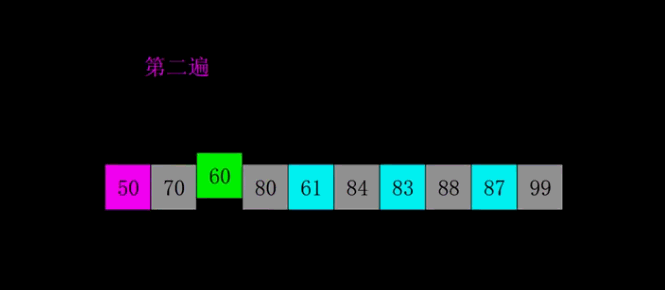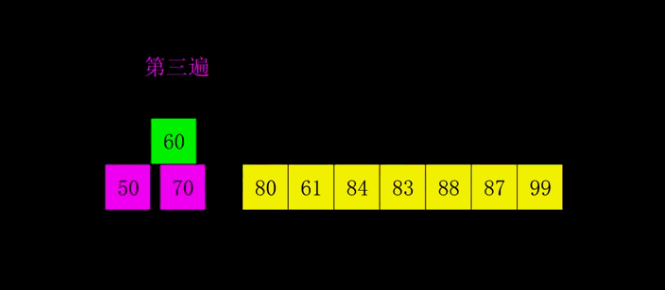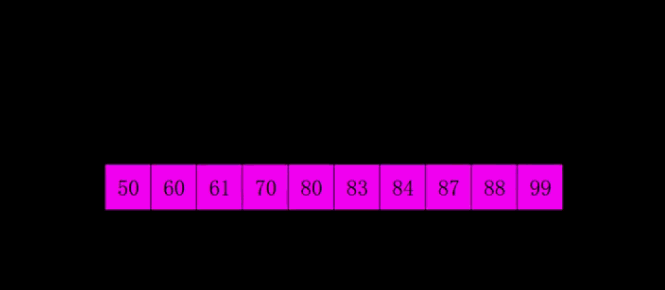
2.3 排序过程
下面以数列{80,30,60,40,20,10,50,70}为例,演示它的希尔排序过程。
第1趟:(gap=4)
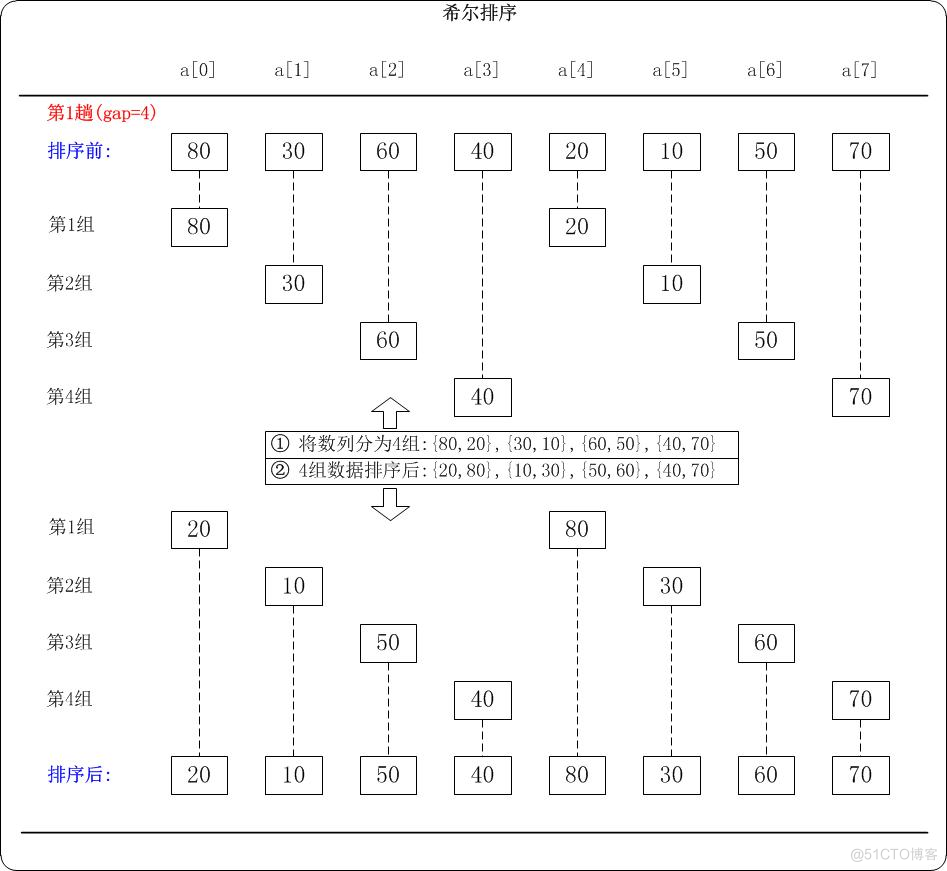
当gap=4时,意味着将数列分为4个组: {80,20},{30,10},{60,50},{40,70}。 对应数列: {80,30,60,40,20,10,50,70}
对这4个组分别进行排序,排序结果: {20,80},{10,30},{50,60},{40,70}。 对应数列: {20,10,50,40,80,30,60,70}
第2趟:(gap=2)
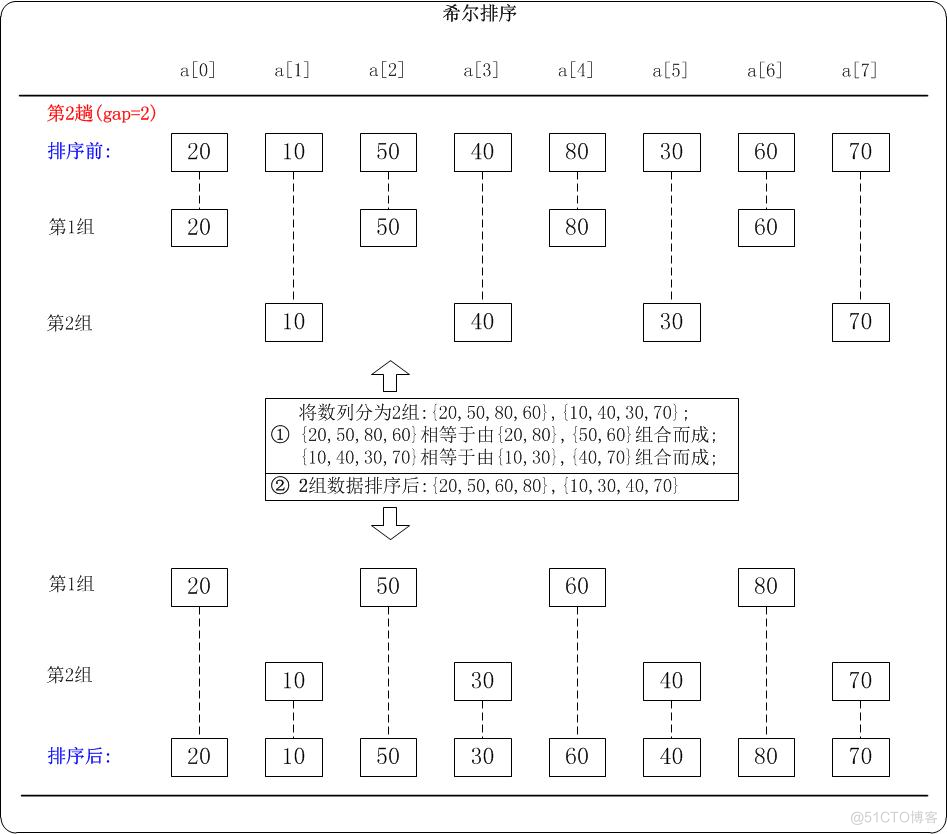
当gap=2时,意味着将数列分为2个组:{20,50,80,60}, {10,40,30,70}。 对应数列: {20,10,50,40,80,30,60,70}
注意:{20,50,80,60}实际上有两个有序的数列{20,80}和{50,60}组成。
{10,40,30,70}实际上有两个有序的数列{10,30}和{40,70}组成。
对这2个组分别进行排序,排序结果:{20,50,60,80}, {10,30,40,70}。 对应数列: {20,10,50,30,60,40,80,70}
第3趟:(gap=1)

当gap=1时,意味着将数列分为1个组:{20,10,50,30,60,40,80,70}
注意:{20,10,50,30,60,40,80,70}实际上有两个有序的数列{20,50,60,80}和{10,30,40,70}组成。
对这1个组分别进行排序,排序结果:{10,20,30,40,50,60,70,80}
2.4 代码实现
2.4.1 常规版(不推荐)
- 外层while循环,代码较为复杂。
- 调整希尔排序的步长需要增加额外代码。
/**
* @Author: huangyibo
* @Date: 2022/2/20 15:35
* @Description: 希尔排序 常规版
*/
public class ShellSort {
public static <E extends Comparable<E>> void shellSort(E[] arr){
//最开始希尔排序的元素间隔,gap增量,并逐步缩小增量
int gap = arr.length / 2;
//外层循环条件
while (gap >= 1){
//start 每一个子数组起始的元素索引,间距为gap
//即每个子数组元素为arr[start, start + gap, start + 2gap, start + 3gap ......]
//即对每个子数组进行插入排序
for (int start = 0; start < gap; start++) {
//即每个子数组元素为arr[start, start + gap, start + 2gap, start + 3gap ......]
//即对每个子数组进行插入排序
for (int i = start + gap; i < arr.length; i += gap) {
//当前待插入的元素
E t = arr[i];
int j;
//从当前元素开始,和当前子数组的前一个元素比较,小于前一个元素,则前一个元素挪到后面
//不断循环,子数组以gap为间隙
for(j = i; j - gap >= 0 && t.compareTo(arr[j - gap]) < 0; j -= gap){
arr[j] = arr[j - gap];
}
//待插入的元素插入到应该的位置
arr[j] = t;
}
}
//每一轮循环之后,
// gap增量逐步缩小,缩小为原来的2分之一,小于1则停止循环
gap /= 2;
}
}
}
2.4.2 常规版优化(不推荐)
- 外层while循环,省略内层一次for循环。
- 调整希尔排序的步长需要增加额外代码。
/**
* @Author: huangyibo
* @Date: 2022/2/20 15:35
* @Description: 希尔排序 优化版,省略内层一次for循环
*/
public class ShellSort {
public static <E extends Comparable<E>> void shellSort(E[] arr){
//最开始希尔排序的元素间隔,gap增量,并逐步缩小增量
int gap = arr.length / 2;
//外层循环条件
while (gap >= 1){
//即每个子数组元素为arr[start, start + gap, start + 2gap, start + 3gap ......]
//即对 arr[gap,n)进行插入排序
for (int i = gap; i < arr.length; i ++) {
//当前待插入的元素
E t = arr[i];
int j;
//从当前元素开始,和当前子数组的前一个元素比较,小于前一个元素,则前一个元素挪到后面
//不断循环,子数组以gap为间隙
for(j = i; j - gap >= 0 && t.compareTo(arr[j - gap]) < 0; j -= gap){
arr[j] = arr[j - gap];
}
//待插入的元素插入到应该的位置
arr[j] = t;
}
//每一轮循环之后,
// gap增量逐步缩小,缩小为原来的2分之一,小于1则停止循环
gap /= 2;
}
}
}
2.4.3 优化版(推荐)
- 针对有序序列在插入时采用交换法。
- 调整希尔排序的步长无需增加额外代码。
/**
* @Author: huangyibo
* @Date: 2022/2/20 15:35
* @Description: 希尔排序 优化版 针对有序序列在插入时采用交换法
*/
public class ShellSort {
public static <E extends Comparable<E>> void shellSort(E[] arr){
//增量gap,并逐步缩小增量, 每一轮缩小为原来的2分之一
//gap的取值可以变化,可以 gap /= 3
for(int gap = arr.length / 2; gap > 0; gap /= 2){
//从第gap个元素,逐个对其所在组进行直接插入排序操作
for(int i = gap; i < arr.length; i++){
int j = i;
while(j - gap >= 0 && arr[j].compareTo(arr[j - gap]) < 0){
//插入排序采用交换法
swap(arr,j,j-gap);
j -= gap;
}
}
}
}
/**
* 交换数组元素
* @param arr
* @param i
* @param j
* @param <E>
*/
private static <E> void swap(E[] arr, int i, int j) {
E temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
2.4.4 优化版(推荐)
- 针对有序序列在插入时采用移动法。
- 调整希尔排序的步长无需增加额外代码。
/**
* @Author: huangyibo
* @Date: 2022/2/20 15:35
* @Description: 希尔排序 优化版 针对有序序列在插入时采用移动法
*/
public class ShellSort {
public static <E extends Comparable<E>> void shellSort(E[] arr){
//增量gap,并逐步缩小增量, 每一轮缩小为原来的2分之一
//gap的取值可以变化,可以 gap /= 3
for(int gap = arr.length / 2; gap > 0; gap /= 2){
//每个子数组元素为arr[start, start + gap, start + 2gap, start + 3gap ......]
//从第gap个元素,逐个对其所在组进行直接插入排序操作
for(int i = gap; i < arr.length; i++){
int j = i;
//当前待插入元素
E temp = arr[j];
//如果待插入元素和当前子数组的前一个元素比较,小于前一个元素,并且索引合法
while(j - gap >= 0 && temp.compareTo(arr[j - gap]) < 0){
//移动法
arr[j] = arr[j-gap];
//将子数组更前的索引赋值给循环变量
j -= gap;
}
//待插入的元素插入到应该的位置
arr[j] = temp;
}
}
}
}
2.5 算法分析
希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列,也可以动态的定义间隔序列。动态定义间隔序列的算法是《算法(第4版)》的合著者Robert Sedgewick提出的。
2.6 希尔排序的时间复杂度和稳定性
希尔排序时间复杂度
希尔排序的时间复杂度与增量(即,步长gap)的选取有关。例如,当增量为1时,希尔排序退化成了直接插入排序,此时的时间复杂度为O(N²),而Hibbard增量的希尔排序的时间复杂度为O(N3/2)。
希尔排序稳定性
希尔排序是不稳定的算法,它满足稳定算法的定义。对于相同的两个数,可能由于分在不同的组中而导致它们的顺序发生变化。
算法稳定性 -- 假设在数列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;并且排序之后,a[i]仍然在a[j]前面。则这个排序算法是稳定的!
参考:
https://www.cnblogs.com/onepixel/articles/7674659.html
https://www.cnblogs.com/skywang12345/p/3597597.html
https://www.cnblogs.com/chengxiao/p/6104371.html






